Towards a Fairer Non-negative Matrix Factorization

Topic modeling, or more broadly, dimensionality reduction, techniques provide powerful tools for uncovering patterns in large datasets and are widely applied across various domains. We investigate how Non-negative Matrix Factorization (NMF) can introduce bias in the representation of data groups, such as those defined by demographics or protected attributes. We present an approach, called Fairer-NMF, that seeks to minimize the maximum reconstruction loss for different groups relative to their size and intrinsic complexity. Further, we present two algorithms for solving this problem. The first is an alternating minimization (AM) scheme and the second is a multiplicative updates (MU) scheme which demonstrates a reduced computational time compared to AM while still achieving similar performance. Lastly, we present numerical experiments on synthetic and real datasets to evaluate the overall performance and trade-offs of Fairer-NMF

TopTemp: Parsing Precipitate Structure from Temper Topology

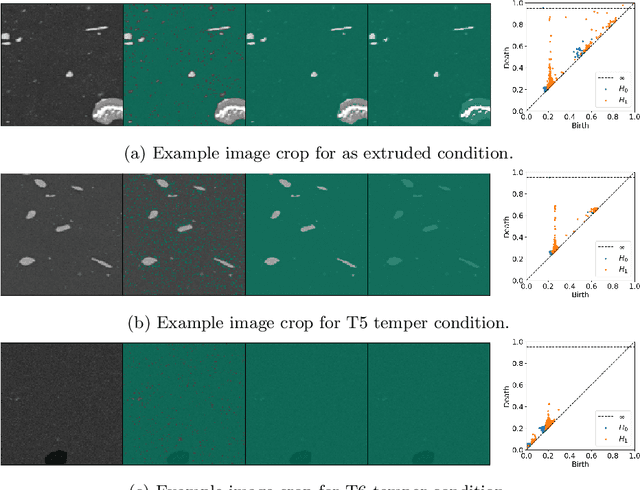
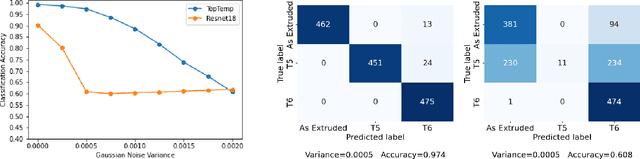
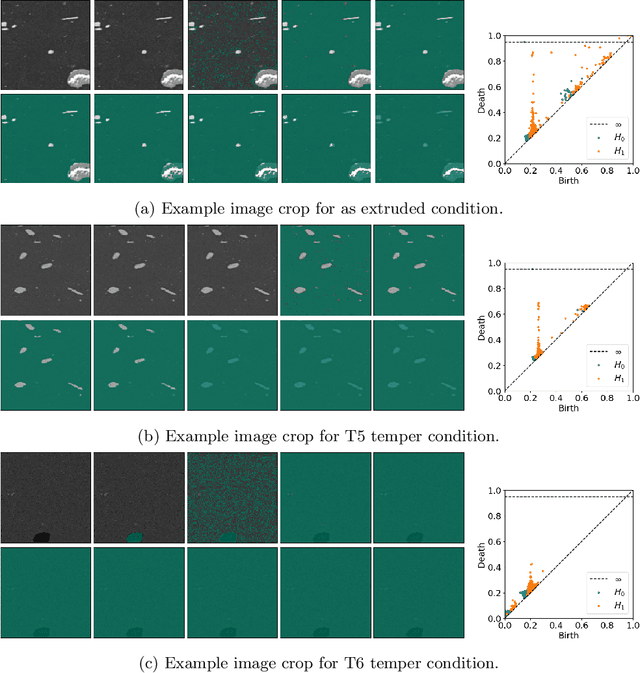
Technological advances are in part enabled by the development of novel manufacturing processes that give rise to new materials or material property improvements. Development and evaluation of new manufacturing methodologies is labor-, time-, and resource-intensive expensive due to complex, poorly defined relationships between advanced manufacturing process parameters and the resulting microstructures. In this work, we present a topological representation of temper (heat-treatment) dependent material micro-structure, as captured by scanning electron microscopy, called TopTemp. We show that this topological representation is able to support temper classification of microstructures in a data limited setting, generalizes well to previously unseen samples, is robust to image perturbations, and captures domain interpretable features. The presented work outperforms conventional deep learning baselines and is a first step towards improving understanding of process parameters and resulting material properties.

Semi-supervised Nonnegative Matrix Factorization for Document Classification

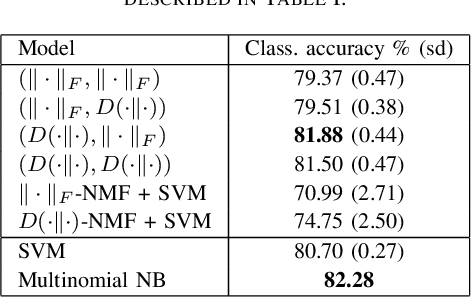
We propose new semi-supervised nonnegative matrix factorization (SSNMF) models for document classification and provide motivation for these models as maximum likelihood estimators. The proposed SSNMF models simultaneously provide both a topic model and a model for classification, thereby offering highly interpretable classification results. We derive training methods using multiplicative updates for each new model, and demonstrate the application of these models to single-label and multi-label document classification, although the models are flexible to other supervised learning tasks such as regression. We illustrate the promise of these models and training methods on document classification datasets (e.g., 20 Newsgroups, Reuters).

Semi-supervised NMF Models for Topic Modeling in Learning Tasks

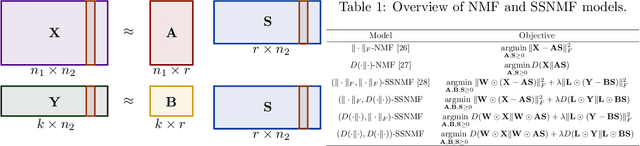
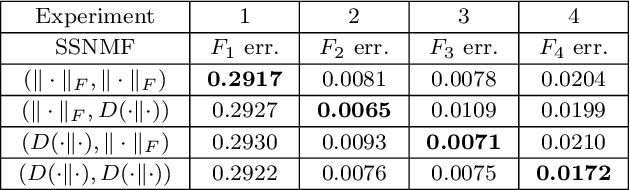
We propose several new models for semi-supervised nonnegative matrix factorization (SSNMF) and provide motivation for SSNMF models as maximum likelihood estimators given specific distributions of uncertainty. We present multiplicative updates training methods for each new model, and demonstrate the application of these models to classification, although they are flexible to other supervised learning tasks. We illustrate the promise of these models and training methods on both synthetic and real data, and achieve high classification accuracy on the 20 Newsgroups dataset.

On Large-Scale Dynamic Topic Modeling with Nonnegative CP Tensor Decomposition

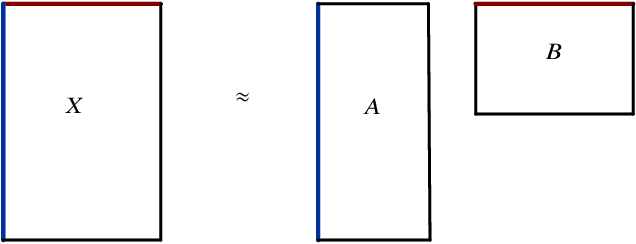
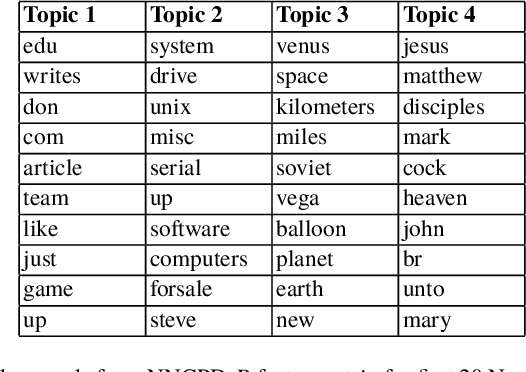
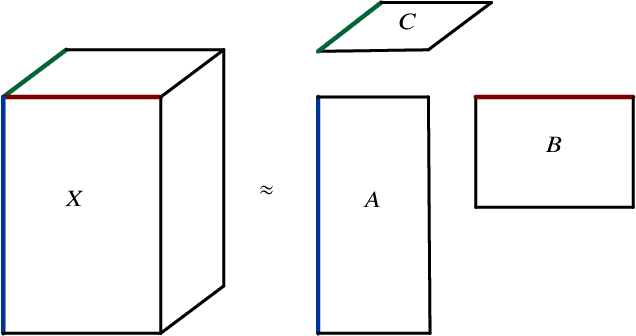
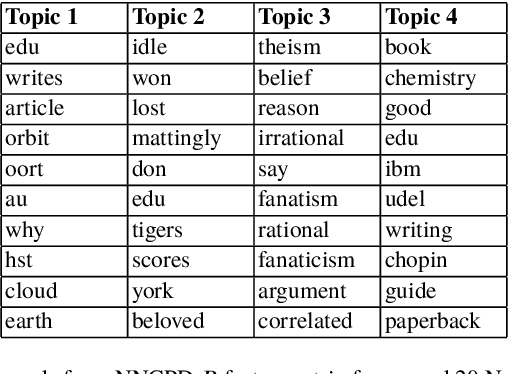
There is currently an unprecedented demand for large-scale temporal data analysis due to the explosive growth of data. Dynamic topic modeling has been widely used in social and data sciences with the goal of learning latent topics that emerge, evolve, and fade over time. Previous work on dynamic topic modeling primarily employ the method of nonnegative matrix factorization (NMF), where slices of the data tensor are each factorized into the product of lower-dimensional nonnegative matrices. With this approach, however, information contained in the temporal dimension of the data is often neglected or underutilized. To overcome this issue, we propose instead adopting the method of nonnegative CANDECOMP/PARAPAC (CP) tensor decomposition (NNCPD), where the data tensor is directly decomposed into a minimal sum of outer products of nonnegative vectors, thereby preserving the temporal information. The viability of NNCPD is demonstrated through application to both synthetic and real data, where significantly improved results are obtained compared to those of typical NMF-based methods. The advantages of NNCPD over such approaches are studied and discussed. To the best of our knowledge, this is the first time that NNCPD has been utilized for the purpose of dynamic topic modeling, and our findings will be transformative for both applications and further developments.

On the Nonlinear Statistics of Optical Flow

In "A naturalistic open source movie for optical flow evaluation," Butler et al. create a database of ground-truth optical flow from the computer-generated video Sintel. We study the high-contrast $3\times 3$ patches from this video, and provide evidence that this dataset is well-modeled by a torus (a nonlinear 2-dimensional manifold). Our main tools are persistent homology and zigzag persistence, which are popular techniques from the field of computational topology. We show that the optical flow torus model is naturally equipped with the structure of a fiber bundle, which is furthermore related to the statistics of range images.