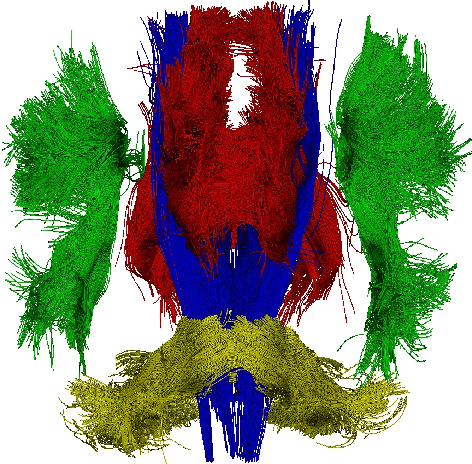
Fast and Scalable Optimal Transport for Brain Tractograms

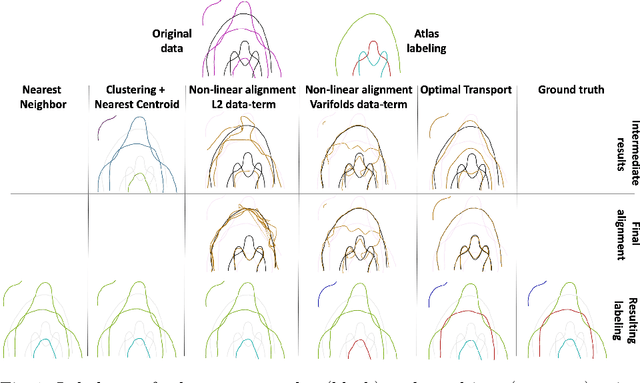
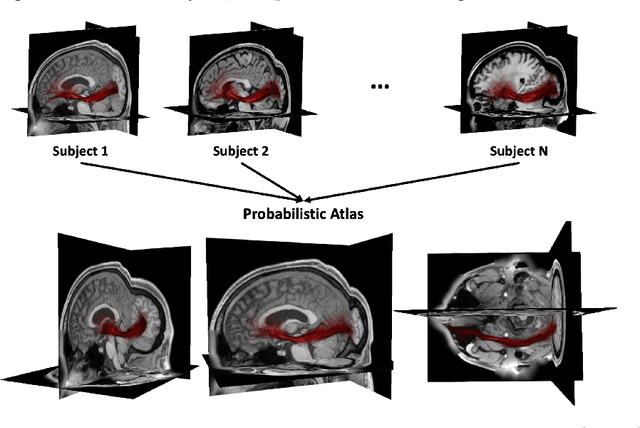
We present a new multiscale algorithm for solving regularized Optimal Transport problems on the GPU, with a linear memory footprint. Relying on Sinkhorn divergences which are convex, smooth and positive definite loss functions, this method enables the computation of transport plans between millions of points in a matter of minutes. We show the effectiveness of this approach on brain tractograms modeled either as bundles of fibers or as track density maps. We use the resulting smooth assignments to perform label transfer for atlas-based segmentation of fiber tractograms. The parameters -- blur and reach -- of our method are meaningful, defining the minimum and maximum distance at which two fibers are compared with each other. They can be set according to anatomical knowledge. Furthermore, we also propose to estimate a probabilistic atlas of a population of track density maps as a Wasserstein barycenter. Our CUDA implementation is endowed with a user-friendly PyTorch interface, freely available on the PyPi repository (pip install geomloss) and at www.kernel-operations.io/geomloss.

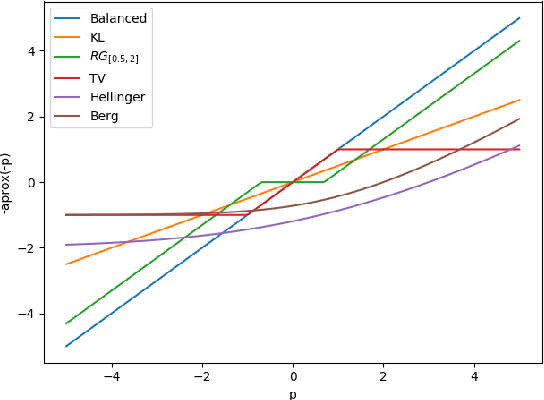
Sinkhorn Divergences for Unbalanced Optimal Transport

This paper extends the formulation of Sinkhorn divergences to the unbalanced setting of arbitrary positive measures, providing both theoretical and algorithmic advances. Sinkhorn divergences leverage the entropic regularization of Optimal Transport (OT) to define geometric loss functions. They are differentiable, cheap to compute and do not suffer from the curse of dimensionality, while maintaining the geometric properties of OT, in particular they metrize the weak$^*$ convergence. Extending these divergences to the unbalanced setting is of utmost importance since most applications in data sciences require to handle both transportation and creation/destruction of mass. This includes for instance problems as diverse as shape registration in medical imaging, density fitting in statistics, generative modeling in machine learning, and particles flows involving birth/death dynamics. Our first set of contributions is the definition and the theoretical analysis of the unbalanced Sinkhorn divergences. They enjoy the same properties as the balanced divergences (classical OT), which are obtained as a special case. Indeed, we show that they are convex, differentiable and metrize the weak$^*$ convergence. Our second set of contributions studies generalized Sinkkhorn iterations, which enable a fast, stable and massively parallelizable algorithm to compute these divergences. We show, under mild assumptions, a linear rate of convergence, independent of the number of samples, i.e. which can cope with arbitrary input measures. We also highlight the versatility of this method, which takes benefit from the latest advances in term of GPU computing, for instance through the KeOps library for fast and scalable kernel operations.

The fshape framework for the variability analysis of functional shapes

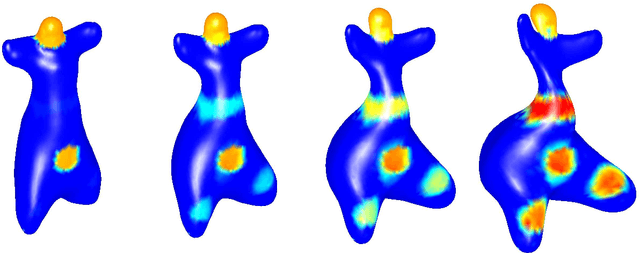
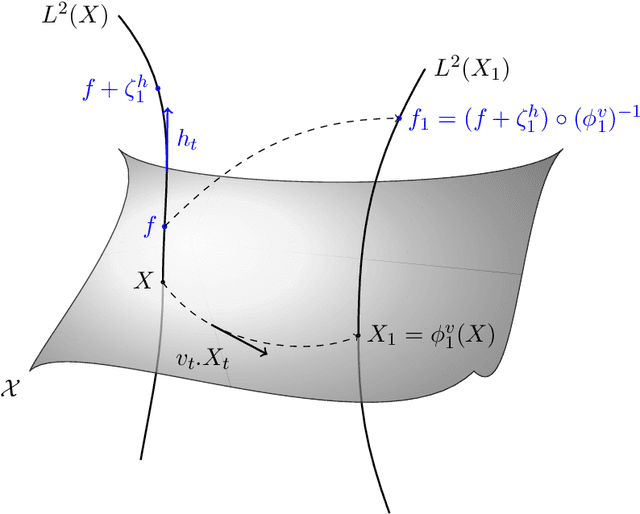
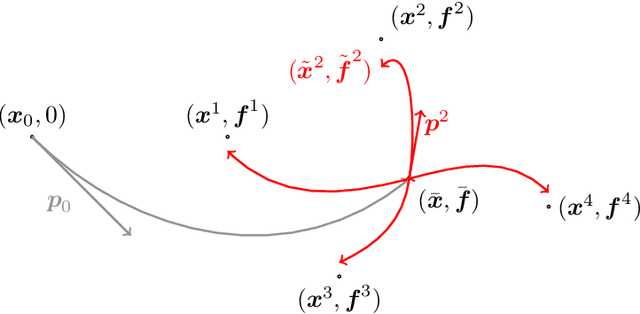
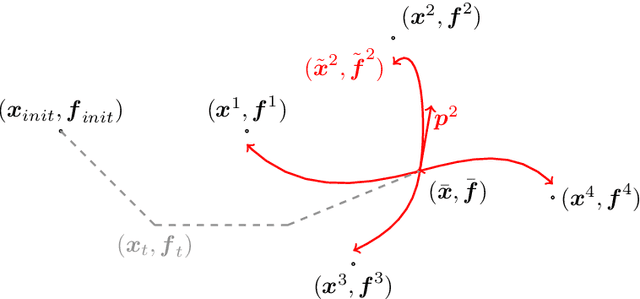
This article introduces a full mathematical and numerical framework for treating functional shapes (or fshapes) following the landmarks of shape spaces and shape analysis. Functional shapes can be described as signal functions supported on varying geometrical supports. Analysing variability of fshapes' ensembles require the modelling and quantification of joint variations in geometry and signal, which have been treated separately in previous approaches. Instead, building on the ideas of shape spaces for purely geometrical objects, we propose the extended concept of fshape bundles and define Riemannian metrics for fshape metamorphoses to model geometrico-functional transformations within these bundles. We also generalize previous works on data attachment terms based on the notion of varifolds and demonstrate the utility of these distances. Based on these, we propose variational formulations of the atlas estimation problem on populations of fshapes and prove existence of solutions for the different models. The second part of the article examines the numerical implementation of the models by detailing discrete expressions for the metrics and gradients and proposing an optimization scheme for the atlas estimation problem. We present a few results of the methodology on a synthetic dataset as well as on a population of retinal membranes with thickness maps.

The varifold representation of non-oriented shapes for diffeomorphic registration

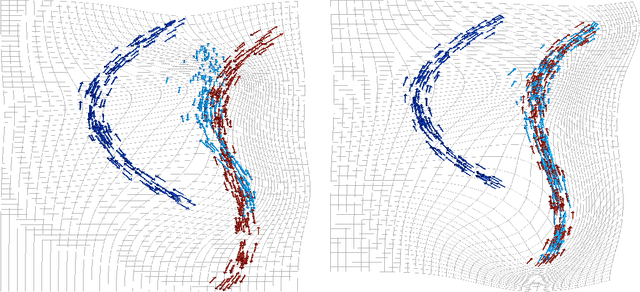
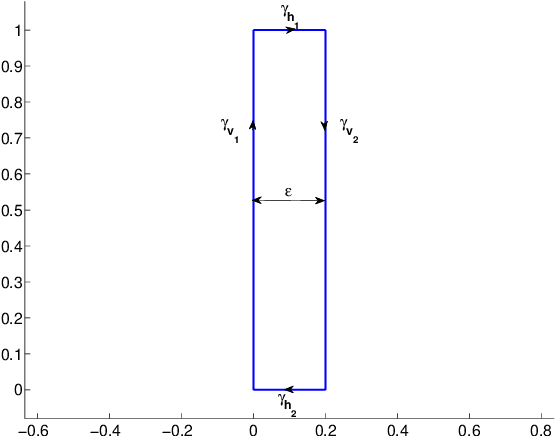
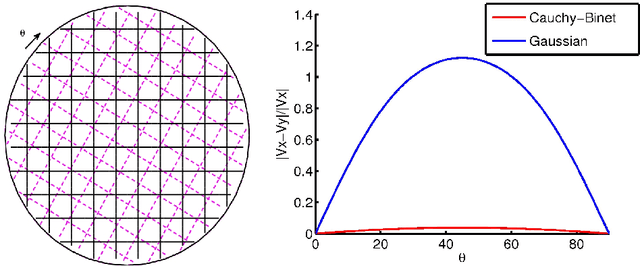
In this paper, we address the problem of orientation that naturally arises when representing shapes like curves or surfaces as currents. In the field of computational anatomy, the framework of currents has indeed proved very efficient to model a wide variety of shapes. However, in such approaches, orientation of shapes is a fundamental issue that can lead to several drawbacks in treating certain kind of datasets. More specifically, problems occur with structures like acute pikes because of canceling effects of currents or with data that consists in many disconnected pieces like fiber bundles for which currents require a consistent orientation of all pieces. As a promising alternative to currents, varifolds, introduced in the context of geometric measure theory by F. Almgren, allow the representation of any non-oriented manifold (more generally any non-oriented rectifiable set). In particular, we explain how varifolds can encode numerically non-oriented objects both from the discrete and continuous point of view. We show various ways to build a Hilbert space structure on the set of varifolds based on the theory of reproducing kernels. We show that, unlike the currents' setting, these metrics are consistent with shape volume (theorem 4.1) and we derive a formula for the variation of metric with respect to the shape (theorem 4.2). Finally, we propose a generalization to non-oriented shapes of registration algorithms in the context of Large Deformations Metric Mapping (LDDMM), which we detail with a few examples in the last part of the paper.

Functional Currents : a new mathematical tool to model and analyse functional shapes

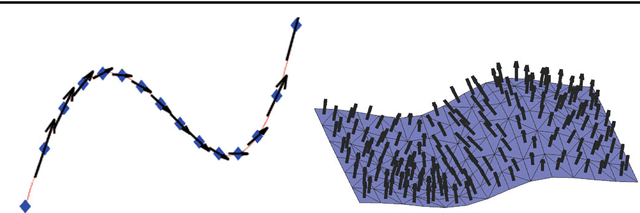
This paper introduces the concept of functional current as a mathematical framework to represent and treat functional shapes, i.e. sub-manifold supported signals. It is motivated by the growing occurrence, in medical imaging and computational anatomy, of what can be described as geometrico-functional data, that is a data structure that involves a deformable shape (roughly a finite dimensional sub manifold) together with a function defined on this shape taking value in another manifold. Indeed, if mathematical currents have already proved to be very efficient theoretically and numerically to model and process shapes as curves or surfaces, they are limited to the manipulation of purely geometrical objects. We show that the introduction of the concept of functional currents offers a genuine solution to the simultaneous processing of the geometric and signal information of any functional shape. We explain how functional currents can be equipped with a Hilbertian norm mixing geometrical and functional content of functional shapes nicely behaving under geometrical and functional perturbations and paving the way to various processing algorithms. We illustrate this potential on two problems: the redundancy reduction of functional shapes representations through matching pursuit schemes on functional currents and the simultaneous geometric and functional registration of functional shapes under diffeomorphic transport.