Stacey: Promoting Stochastic Steepest Descent via Accelerated $\ell_p$-Smooth Nonconvex Optimization

While popular optimization methods such as SGD, AdamW, and Lion depend on steepest descent updates in either $\ell_2$ or $\ell_\infty$ norms, there remains a critical gap in handling the non-Euclidean structure observed in modern deep networks training. In this work, we address this need by introducing a new accelerated $\ell_p$ steepest descent algorithm, called Stacey, which uses interpolated primal-dual iterate sequences to effectively navigate non-Euclidean smooth optimization tasks. In addition to providing novel theoretical guarantees for the foundations of our algorithm, we empirically compare our approach against these popular methods on tasks including image classification and language model (LLM) pretraining, demonstrating both faster convergence and higher final accuracy. We further evaluate different values of $p$ across various models and datasets, underscoring the importance and efficiency of non-Euclidean approaches over standard Euclidean methods. Code can be found at https://github.com/xinyuluo8561/Stacey .

Trustworthy Reputation Games and Applications to Proof-of-Reputation Blockchains

Reputation systems play an essential role in the Internet era, as they enable people to decide whom to trust, by collecting and aggregating data about users' behavior. Recently, several works proposed the use of reputation for the design and scalability improvement of decentralized (blockchain) ledgers; however, such systems are prone to manipulation and to our knowledge no game-theoretic treatment exists that can support their economic robustness. In this work we put forth a new model for the design of what we call, {\em trustworthy reputation systems}. Concretely, we describe a class of games, which we term {\em trustworthy reputation games}, that enable a set of users to report a function of their beliefs about the trustworthiness of each server in a set -- i.e., their estimate of the probability that this server will behave according to its specified strategy -- in a way that satisfies the following properties: 1. It is $(\epsilon$-)best response for any rational user in the game to play a prescribed (truthful) strategy according to their true belief. 2. Assuming that the users' beliefs are not too far from the {\em true} trustworthiness of the servers, playing the above ($\epsilon-$)Nash equilibrium allows anyone who observes the users' strategies to estimate the relative trustworthiness of any two servers. Our utilities and decoding function build on a connection between the well known PageRank algorithm and the problem of trustworthiness discovery, which can be of independent interest. Finally, we show how the above games are motivated by and can be leveraged in proof-of-reputation (PoR) blockchains.

The Space Complexity of Approximating Logistic Loss

We provide space complexity lower bounds for data structures that approximate logistic loss up to $\epsilon$-relative error on a logistic regression problem with data $\mathbf{X} \in \mathbb{R}^{n \times d}$ and labels $\mathbf{y} \in \{-1,1\}^d$. The space complexity of existing coreset constructions depend on a natural complexity measure $\mu_\mathbf{y}(\mathbf{X})$, first defined in (Munteanu, 2018). We give an $\tilde{\Omega}(\frac{d}{\epsilon^2})$ space complexity lower bound in the regime $\mu_\mathbf{y}(\mathbf{X}) = O(1)$ that shows existing coresets are optimal in this regime up to lower order factors. We also prove a general $\tilde{\Omega}(d\cdot \mu_\mathbf{y}(\mathbf{X}))$ space lower bound when $\epsilon$ is constant, showing that the dependency on $\mu_\mathbf{y}(\mathbf{X})$ is not an artifact of mergeable coresets. Finally, we refute a prior conjecture that $\mu_\mathbf{y}(\mathbf{X})$ is hard to compute by providing an efficient linear programming formulation, and we empirically compare our algorithm to prior approximate methods.

Stochastic Rounding Implicitly Regularizes Tall-and-Thin Matrices

Motivated by the popularity of stochastic rounding in the context of machine learning and the training of large-scale deep neural network models, we consider stochastic nearness rounding of real matrices $\mathbf{A}$ with many more rows than columns. We provide novel theoretical evidence, supported by extensive experimental evaluation that, with high probability, the smallest singular value of a stochastically rounded matrix is well bounded away from zero -- regardless of how close $\mathbf{A}$ is to being rank deficient and even if $\mathbf{A}$ is rank-deficient. In other words, stochastic rounding \textit{implicitly regularizes} tall and skinny matrices $\mathbf{A}$ so that the rounded version has full column rank. Our proofs leverage powerful results in random matrix theory, and the idea that stochastic rounding errors do not concentrate in low-dimensional column spaces.

Sketching Algorithms for Sparse Dictionary Learning: PTAS and Turnstile Streaming

Sketching algorithms have recently proven to be a powerful approach both for designing low-space streaming algorithms as well as fast polynomial time approximation schemes (PTAS). In this work, we develop new techniques to extend the applicability of sketching-based approaches to the sparse dictionary learning and the Euclidean $k$-means clustering problems. In particular, we initiate the study of the challenging setting where the dictionary/clustering assignment for each of the $n$ input points must be output, which has surprisingly received little attention in prior work. On the fast algorithms front, we obtain a new approach for designing PTAS's for the $k$-means clustering problem, which generalizes to the first PTAS for the sparse dictionary learning problem. On the streaming algorithms front, we obtain new upper bounds and lower bounds for dictionary learning and $k$-means clustering. In particular, given a design matrix $\mathbf A\in\mathbb R^{n\times d}$ in a turnstile stream, we show an $\tilde O(nr/\epsilon^2 + dk/\epsilon)$ space upper bound for $r$-sparse dictionary learning of size $k$, an $\tilde O(n/\epsilon^2 + dk/\epsilon)$ space upper bound for $k$-means clustering, as well as an $\tilde O(n)$ space upper bound for $k$-means clustering on random order row insertion streams with a natural "bounded sensitivity" assumption. On the lower bounds side, we obtain a general $\tilde\Omega(n/\epsilon + dk/\epsilon)$ lower bound for $k$-means clustering, as well as an $\tilde\Omega(n/\epsilon^2)$ lower bound for algorithms which can estimate the cost of a single fixed set of candidate centers.

Refined Mechanism Design for Approximately Structured Priors via Active Regression

We consider the problem of a revenue-maximizing seller with a large number of items $m$ for sale to $n$ strategic bidders, whose valuations are drawn independently from high-dimensional, unknown prior distributions. It is well-known that optimal and even approximately-optimal mechanisms for this setting are notoriously difficult to characterize or compute, and, even when they can be found, are often rife with various counter-intuitive properties. In this paper, following a model introduced recently by Cai and Daskalakis~\cite{cai2022recommender}, we consider the case that bidders' prior distributions can be well-approximated by a topic model. We design an active learning component, responsible for interacting with the bidders and outputting low-dimensional approximations of their types, and a mechanism design component, responsible for robustifying mechanisms for the low-dimensional model to work for the approximate types of the former component. On the active learning front, we cast our problem in the framework of Randomized Linear Algebra (RLA) for regression problems, allowing us to import several breakthrough results from that line of research, and adapt them to our setting. On the mechanism design front, we remove many restrictive assumptions of prior work on the type of access needed to the underlying distributions and the associated mechanisms. To the best of our knowledge, our work is the first to formulate connections between mechanism design, and RLA for active learning of regression problems, opening the door for further applications of randomized linear algebra primitives to mechanism design.

Feature Space Sketching for Logistic Regression

We present novel bounds for coreset construction, feature selection, and dimensionality reduction for logistic regression. All three approaches can be thought of as sketching the logistic regression inputs. On the coreset construction front, we resolve open problems from prior work and present novel bounds for the complexity of coreset construction methods. On the feature selection and dimensionality reduction front, we initiate the study of forward error bounds for logistic regression. Our bounds are tight up to constant factors and our forward error bounds can be extended to Generalized Linear Models.

Low-Rank Updates of Matrix Square Roots

Models in which the covariance matrix has the structure of a sparse matrix plus a low rank perturbation are ubiquitous in machine learning applications. It is often desirable for learning algorithms to take advantage of such structures, avoiding costly matrix computations that often require cubic time and quadratic storage. This is often accomplished by performing operations that maintain such structures, e.g. matrix inversion via the Sherman-Morrison-Woodbury formula. In this paper we consider the matrix square root and inverse square root operations. Given a low rank perturbation to a matrix, we argue that a low-rank approximate correction to the (inverse) square root exists. We do so by establishing a geometric decay bound on the true correction's eigenvalues. We then proceed to frame the correction has the solution of an algebraic Ricatti equation, and discuss how a low-rank solution to that equation can be computed. We analyze the approximation error incurred when approximately solving the algebraic Ricatti equation, providing spectral and Frobenius norm forward and backward error bounds. Finally, we describe several applications of our algorithms, and demonstrate their utility in numerical experiments.

Approximation Algorithms for Sparse Principal Component Analysis

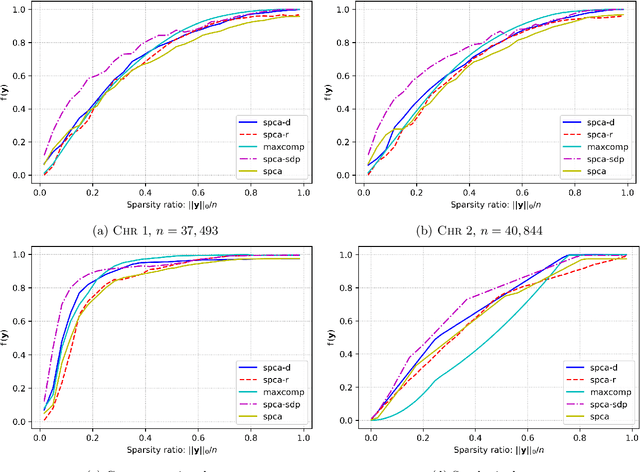
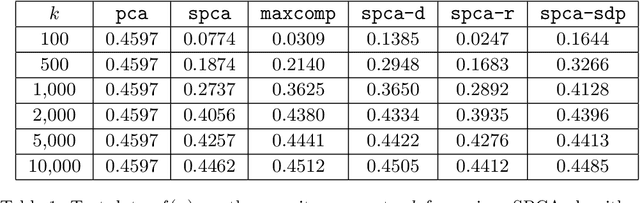
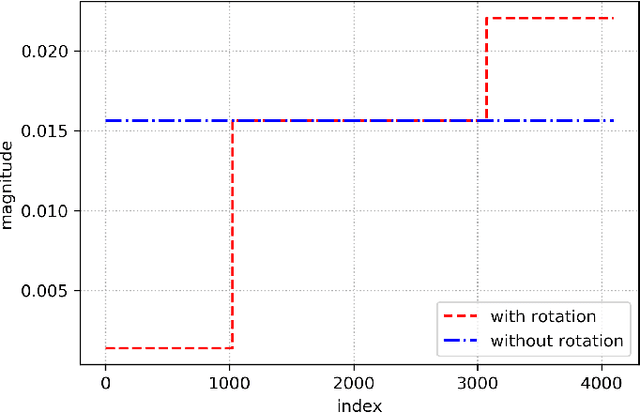
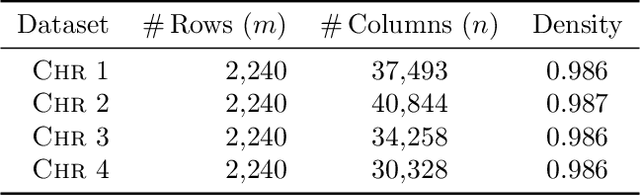
We present three provably accurate, polynomial time, approximation algorithms for the Sparse Principal Component Analysis (SPCA) problem, without imposing any restrictive assumptions on the input covariance matrix. The first algorithm is based on randomized matrix multiplication; the second algorithm is based on a novel deterministic thresholding scheme; and the third algorithm is based on a semidefinite programming relaxation of SPCA. All algorithms come with provable guarantees and run in low-degree polynomial time. Our empirical evaluations confirm our theoretical findings.

Randomized Iterative Algorithms for Fisher Discriminant Analysis

Fisher discriminant analysis (FDA) is a widely used method for classification and dimensionality reduction. When the number of predictor variables greatly exceeds the number of observations, one of the alternatives for conventional FDA is regularized Fisher discriminant analysis (RFDA). In this paper, we present a simple, iterative, sketching-based algorithm for RFDA that comes with provable accuracy guarantees when compared to the conventional approach. Our analysis builds upon two simple structural results that boil down to randomized matrix multiplication, a fundamental and well-understood primitive of randomized linear algebra. We analyze the behavior of RFDA when the ridge leverage and the standard leverage scores are used to select predictor variables and we prove that accurate approximations can be achieved by a sample whose size depends on the effective degrees of freedom of the RFDA problem. Our results yield significant improvements over existing approaches and our empirical evaluations support our theoretical analyses.