Euclidean, Projective, Conformal: Choosing a Geometric Algebra for Equivariant Transformers

The Geometric Algebra Transformer (GATr) is a versatile architecture for geometric deep learning based on projective geometric algebra. We generalize this architecture into a blueprint that allows one to construct a scalable transformer architecture given any geometric (or Clifford) algebra. We study versions of this architecture for Euclidean, projective, and conformal algebras, all of which are suited to represent 3D data, and evaluate them in theory and practice. The simplest Euclidean architecture is computationally cheap, but has a smaller symmetry group and is not as sample-efficient, while the projective model is not sufficiently expressive. Both the conformal algebra and an improved version of the projective algebra define powerful, performant architectures.

Uncertainty-driven Affordance Discovery for Efficient Robotics Manipulation

Robotics affordances, providing information about what actions can be taken in a given situation, can aid robotics manipulation. However, learning about affordances requires expensive large annotated datasets of interactions or demonstrations. In this work, we show active learning can mitigate this problem and propose the use of uncertainty to drive an interactive affordance discovery process. We show that our method enables the efficient discovery of visual affordances for several action primitives, such as grasping, stacking objects, or opening drawers, strongly improving data efficiency and allowing us to learn grasping affordances on a real-world setup with an xArm 6 robot arm in a small number of trials.

BISCUIT: Causal Representation Learning from Binary Interactions

Identifying the causal variables of an environment and how to intervene on them is of core value in applications such as robotics and embodied AI. While an agent can commonly interact with the environment and may implicitly perturb the behavior of some of these causal variables, often the targets it affects remain unknown. In this paper, we show that causal variables can still be identified for many common setups, e.g., additive Gaussian noise models, if the agent's interactions with a causal variable can be described by an unknown binary variable. This happens when each causal variable has two different mechanisms, e.g., an observational and an interventional one. Using this identifiability result, we propose BISCUIT, a method for simultaneously learning causal variables and their corresponding binary interaction variables. On three robotic-inspired datasets, BISCUIT accurately identifies causal variables and can even be scaled to complex, realistic environments for embodied AI.

Geometric Algebra Transformers

Problems involving geometric data arise in a variety of fields, including computer vision, robotics, chemistry, and physics. Such data can take numerous forms, such as points, direction vectors, planes, or transformations, but to date there is no single architecture that can be applied to such a wide variety of geometric types while respecting their symmetries. In this paper we introduce the Geometric Algebra Transformer (GATr), a general-purpose architecture for geometric data. GATr represents inputs, outputs, and hidden states in the projective geometric algebra, which offers an efficient 16-dimensional vector space representation of common geometric objects as well as operators acting on them. GATr is equivariant with respect to E(3), the symmetry group of 3D Euclidean space. As a transformer, GATr is scalable, expressive, and versatile. In experiments with n-body modeling and robotic planning, GATr shows strong improvements over non-geometric baselines.

EDGI: Equivariant Diffusion for Planning with Embodied Agents

Embodied agents operate in a structured world, often solving tasks with spatial, temporal, and permutation symmetries. Most algorithms for planning and model-based reinforcement learning (MBRL) do not take this rich geometric structure into account, leading to sample inefficiency and poor generalization. We introduce the Equivariant Diffuser for Generating Interactions (EDGI), an algorithm for MBRL and planning that is equivariant with respect to the product of the spatial symmetry group $\mathrm{SE(3)}$, the discrete-time translation group $\mathbb{Z}$, and the object permutation group $\mathrm{S}_n$. EDGI follows the Diffuser framework (Janner et al. 2022) in treating both learning a world model and planning in it as a conditional generative modeling problem, training a diffusion model on an offline trajectory dataset. We introduce a new $\mathrm{SE(3)} \times \mathbb{Z} \times \mathrm{S}_n$-equivariant diffusion model that supports multiple representations. We integrate this model in a planning loop, where conditioning and classifier-based guidance allow us to softly break the symmetry for specific tasks as needed. On navigation and object manipulation tasks, EDGI improves sample efficiency and generalization.

On the Expressive Power of Geometric Graph Neural Networks

The expressive power of Graph Neural Networks (GNNs) has been studied extensively through the Weisfeiler-Leman (WL) graph isomorphism test. However, standard GNNs and the WL framework are inapplicable for geometric graphs embedded in Euclidean space, such as biomolecules, materials, and other physical systems. In this work, we propose a geometric version of the WL test (GWL) for discriminating geometric graphs while respecting the underlying physical symmetries: permutations, rotation, reflection, and translation. We use GWL to characterise the expressive power of geometric GNNs that are invariant or equivariant to physical symmetries in terms of distinguishing geometric graphs. GWL unpacks how key design choices influence geometric GNN expressivity: (1) Invariant layers have limited expressivity as they cannot distinguish one-hop identical geometric graphs; (2) Equivariant layers distinguish a larger class of graphs by propagating geometric information beyond local neighbourhoods; (3) Higher order tensors and scalarisation enable maximally powerful geometric GNNs; and (4) GWL's discrimination-based perspective is equivalent to universal approximation. Synthetic experiments supplementing our results are available at https://github.com/chaitjo/geometric-gnn-dojo

Deconfounded Imitation Learning

Standard imitation learning can fail when the expert demonstrators have different sensory inputs than the imitating agent. This is because partial observability gives rise to hidden confounders in the causal graph. We break down the space of confounded imitation learning problems and identify three settings with different data requirements in which the correct imitation policy can be identified. We then introduce an algorithm for deconfounded imitation learning, which trains an inference model jointly with a latent-conditional policy. At test time, the agent alternates between updating its belief over the latent and acting under the belief. We show in theory and practice that this algorithm converges to the correct interventional policy, solves the confounding issue, and can under certain assumptions achieve an asymptotically optimal imitation performance.

A PAC-Bayesian Generalization Bound for Equivariant Networks

Equivariant networks capture the inductive bias about the symmetry of the learning task by building those symmetries into the model. In this paper, we study how equivariance relates to generalization error utilizing PAC Bayesian analysis for equivariant networks, where the transformation laws of feature spaces are determined by group representations. By using perturbation analysis of equivariant networks in Fourier domain for each layer, we derive norm-based PAC-Bayesian generalization bounds. The bound characterizes the impact of group size, and multiplicity and degree of irreducible representations on the generalization error and thereby provide a guideline for selecting them. In general, the bound indicates that using larger group size in the model improves the generalization error substantiated by extensive numerical experiments.

Towards a Grounded Theory of Causation for Embodied AI

There exist well-developed frameworks for causal modelling, but these require rather a lot of human domain expertise to define causal variables and perform interventions. In order to enable autonomous agents to learn abstract causal models through interactive experience, the existing theoretical foundations need to be extended and clarified. Existing frameworks give no guidance regarding variable choice / representation, and more importantly, give no indication as to which behaviour policies or physical transformations of state space shall count as interventions. The framework sketched in this paper describes actions as transformations of state space, for instance induced by an agent running a policy. This makes it possible to describe in a uniform way both transformations of the micro-state space and abstract models thereof, and say when the latter is veridical / grounded / natural. We then introduce (causal) variables, define a mechanism as an invariant predictor, and say when an action can be viewed as a ``surgical intervention'', thus bringing the objective of causal representation & intervention skill learning into clearer focus.

iCITRIS: Causal Representation Learning for Instantaneous Temporal Effects

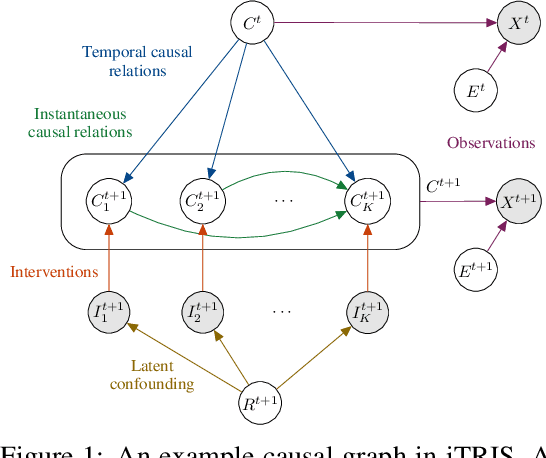
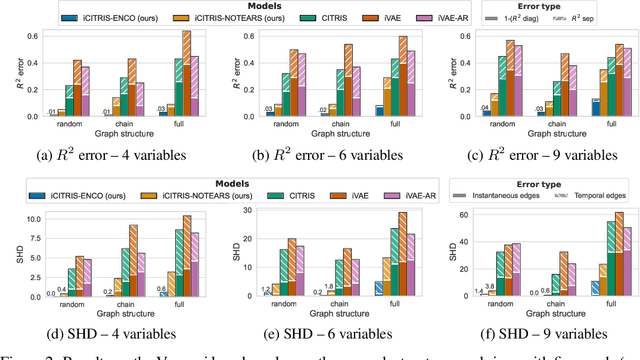
Causal representation learning is the task of identifying the underlying causal variables and their relations from high-dimensional observations, such as images. Recent work has shown that one can reconstruct the causal variables from temporal sequences of observations under the assumption that there are no instantaneous causal relations between them. In practical applications, however, our measurement or frame rate might be slower than many of the causal effects. This effectively creates "instantaneous" effects and invalidates previous identifiability results. To address this issue, we propose iCITRIS, a causal representation learning method that can handle instantaneous effects in temporal sequences when given perfect interventions with known intervention targets. iCITRIS identifies the causal factors from temporal observations, while simultaneously using a differentiable causal discovery method to learn their causal graph. In experiments on three video datasets, iCITRIS accurately identifies the causal factors and their causal graph.