A Lorentz-Equivariant Transformer for All of the LHC

We show that the Lorentz-Equivariant Geometric Algebra Transformer (L-GATr) yields state-of-the-art performance for a wide range of machine learning tasks at the Large Hadron Collider. L-GATr represents data in a geometric algebra over space-time and is equivariant under Lorentz transformations. The underlying architecture is a versatile and scalable transformer, which is able to break symmetries if needed. We demonstrate the power of L-GATr for amplitude regression and jet classification, and then benchmark it as the first Lorentz-equivariant generative network. For all three LHC tasks, we find significant improvements over previous architectures.

Does equivariance matter at scale?

Given large data sets and sufficient compute, is it beneficial to design neural architectures for the structure and symmetries of each problem? Or is it more efficient to learn them from data? We study empirically how equivariant and non-equivariant networks scale with compute and training samples. Focusing on a benchmark problem of rigid-body interactions and on general-purpose transformer architectures, we perform a series of experiments, varying the model size, training steps, and dataset size. We find evidence for three conclusions. First, equivariance improves data efficiency, but training non-equivariant models with data augmentation can close this gap given sufficient epochs. Second, scaling with compute follows a power law, with equivariant models outperforming non-equivariant ones at each tested compute budget. Finally, the optimal allocation of a compute budget onto model size and training duration differs between equivariant and non-equivariant models.

Probabilistic and Differentiable Wireless Simulation with Geometric Transformers

Modelling the propagation of electromagnetic signals is critical for designing modern communication systems. While there are precise simulators based on ray tracing, they do not lend themselves to solving inverse problems or the integration in an automated design loop. We propose to address these challenges through differentiable neural surrogates that exploit the geometric aspects of the problem. We first introduce the Wireless Geometric Algebra Transformer (Wi-GATr), a generic backbone architecture for simulating wireless propagation in a 3D environment. It uses versatile representations based on geometric algebra and is equivariant with respect to E(3), the symmetry group of the underlying physics. Second, we study two algorithmic approaches to signal prediction and inverse problems based on differentiable predictive modelling and diffusion models. We show how these let us predict received power, localize receivers, and reconstruct the 3D environment from the received signal. Finally, we introduce two large, geometry-focused datasets of wireless signal propagation in indoor scenes. In experiments, we show that our geometry-forward approach achieves higher-fidelity predictions with less data than various baselines.

Lorentz-Equivariant Geometric Algebra Transformers for High-Energy Physics

Extracting scientific understanding from particle-physics experiments requires solving diverse learning problems with high precision and good data efficiency. We propose the Lorentz Geometric Algebra Transformer (L-GATr), a new multi-purpose architecture for high-energy physics. L-GATr represents high-energy data in a geometric algebra over four-dimensional space-time and is equivariant under Lorentz transformations, the symmetry group of relativistic kinematics. At the same time, the architecture is a Transformer, which makes it versatile and scalable to large systems. L-GATr is first demonstrated on regression and classification tasks from particle physics. We then construct the first Lorentz-equivariant generative model: a continuous normalizing flow based on an L-GATr network, trained with Riemannian flow matching. Across our experiments, L-GATr is on par with or outperforms strong domain-specific baselines.

FoMo Rewards: Can we cast foundation models as reward functions?

We explore the viability of casting foundation models as generic reward functions for reinforcement learning. To this end, we propose a simple pipeline that interfaces an off-the-shelf vision model with a large language model. Specifically, given a trajectory of observations, we infer the likelihood of an instruction describing the task that the user wants an agent to perform. We show that this generic likelihood function exhibits the characteristics ideally expected from a reward function: it associates high values with the desired behaviour and lower values for several similar, but incorrect policies. Overall, our work opens the possibility of designing open-ended agents for interactive tasks via foundation models.

Euclidean, Projective, Conformal: Choosing a Geometric Algebra for Equivariant Transformers

The Geometric Algebra Transformer (GATr) is a versatile architecture for geometric deep learning based on projective geometric algebra. We generalize this architecture into a blueprint that allows one to construct a scalable transformer architecture given any geometric (or Clifford) algebra. We study versions of this architecture for Euclidean, projective, and conformal algebras, all of which are suited to represent 3D data, and evaluate them in theory and practice. The simplest Euclidean architecture is computationally cheap, but has a smaller symmetry group and is not as sample-efficient, while the projective model is not sufficiently expressive. Both the conformal algebra and an improved version of the projective algebra define powerful, performant architectures.

Geometric Algebra Transformers

Problems involving geometric data arise in a variety of fields, including computer vision, robotics, chemistry, and physics. Such data can take numerous forms, such as points, direction vectors, planes, or transformations, but to date there is no single architecture that can be applied to such a wide variety of geometric types while respecting their symmetries. In this paper we introduce the Geometric Algebra Transformer (GATr), a general-purpose architecture for geometric data. GATr represents inputs, outputs, and hidden states in the projective geometric algebra, which offers an efficient 16-dimensional vector space representation of common geometric objects as well as operators acting on them. GATr is equivariant with respect to E(3), the symmetry group of 3D Euclidean space. As a transformer, GATr is scalable, expressive, and versatile. In experiments with n-body modeling and robotic planning, GATr shows strong improvements over non-geometric baselines.

EDGI: Equivariant Diffusion for Planning with Embodied Agents

Embodied agents operate in a structured world, often solving tasks with spatial, temporal, and permutation symmetries. Most algorithms for planning and model-based reinforcement learning (MBRL) do not take this rich geometric structure into account, leading to sample inefficiency and poor generalization. We introduce the Equivariant Diffuser for Generating Interactions (EDGI), an algorithm for MBRL and planning that is equivariant with respect to the product of the spatial symmetry group $\mathrm{SE(3)}$, the discrete-time translation group $\mathbb{Z}$, and the object permutation group $\mathrm{S}_n$. EDGI follows the Diffuser framework (Janner et al. 2022) in treating both learning a world model and planning in it as a conditional generative modeling problem, training a diffusion model on an offline trajectory dataset. We introduce a new $\mathrm{SE(3)} \times \mathbb{Z} \times \mathrm{S}_n$-equivariant diffusion model that supports multiple representations. We integrate this model in a planning loop, where conditioning and classifier-based guidance allow us to softly break the symmetry for specific tasks as needed. On navigation and object manipulation tasks, EDGI improves sample efficiency and generalization.

Deconfounded Imitation Learning

Standard imitation learning can fail when the expert demonstrators have different sensory inputs than the imitating agent. This is because partial observability gives rise to hidden confounders in the causal graph. We break down the space of confounded imitation learning problems and identify three settings with different data requirements in which the correct imitation policy can be identified. We then introduce an algorithm for deconfounded imitation learning, which trains an inference model jointly with a latent-conditional policy. At test time, the agent alternates between updating its belief over the latent and acting under the belief. We show in theory and practice that this algorithm converges to the correct interventional policy, solves the confounding issue, and can under certain assumptions achieve an asymptotically optimal imitation performance.

Weakly supervised causal representation learning

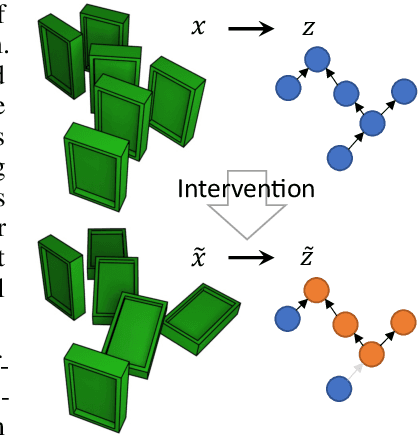
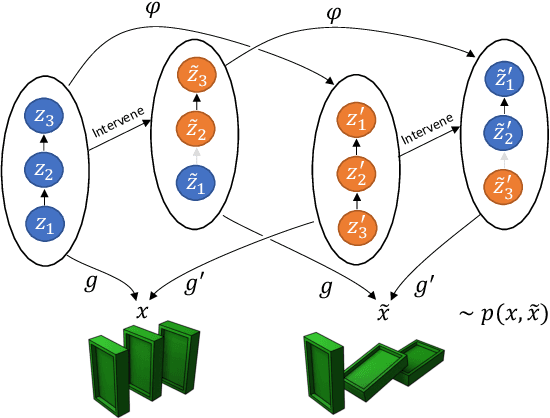
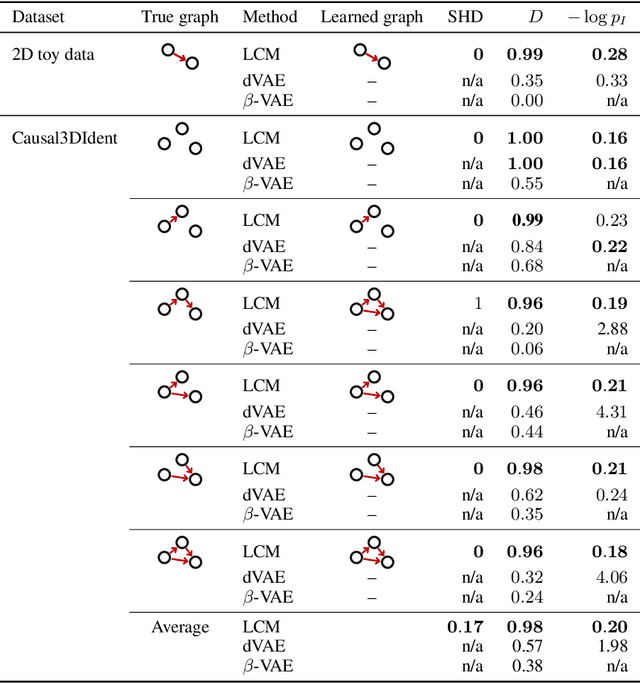
Learning high-level causal representations together with a causal model from unstructured low-level data such as pixels is impossible from observational data alone. We prove under mild assumptions that this representation is identifiable in a weakly supervised setting. This requires a dataset with paired samples before and after random, unknown interventions, but no further labels. Finally, we show that we can infer the representation and causal graph reliably in a simple synthetic domain using a variational autoencoder with a structural causal model as prior.