Relative Navigation and Dynamic Target Tracking for Autonomous Underwater Proximity Operations

Estimating a target's 6-DoF motion in underwater proximity operations is difficult because the chaser lacks target-side proprioception and the available relative observations are sparse, noisy, and often partial (e.g., Ultra-Short Baseline (USBL) positions). Without a motion prior, factor-graph maximum a posteriori estimation is underconstrained: consecutive target states are weakly linked and orientation can drift. We propose a generalized constant-twist motion prior defined on the tangent space of Lie groups that enforces temporally consistent trajectories across all degrees of freedom; in SE(3) it couples translation and rotation in the body frame. We present a ternary factor and derive its closed-form Jacobians based on standard Lie group operations, enabling drop-in use for trajectories on arbitrary Lie groups. We evaluate two deployment modes: (A) an SE(3)-only representation that regularizes orientation even when only position is measured, and (B) a mode with boundary factors that switches the target representation between SE(3) and 3D position while applying the same generalized constant-twist prior across representation changes. Validation on a real-world dynamic docking scenario dataset shows consistent ego-target trajectory estimation through USBL-only and optical relative measurement segments with an improved relative tracking accuracy compared to the noisy measurements to the target. Because the construction relies on standard Lie group primitives, it is portable across state manifolds and sensing modalities.

Robust Frequency-Based Structure Extraction

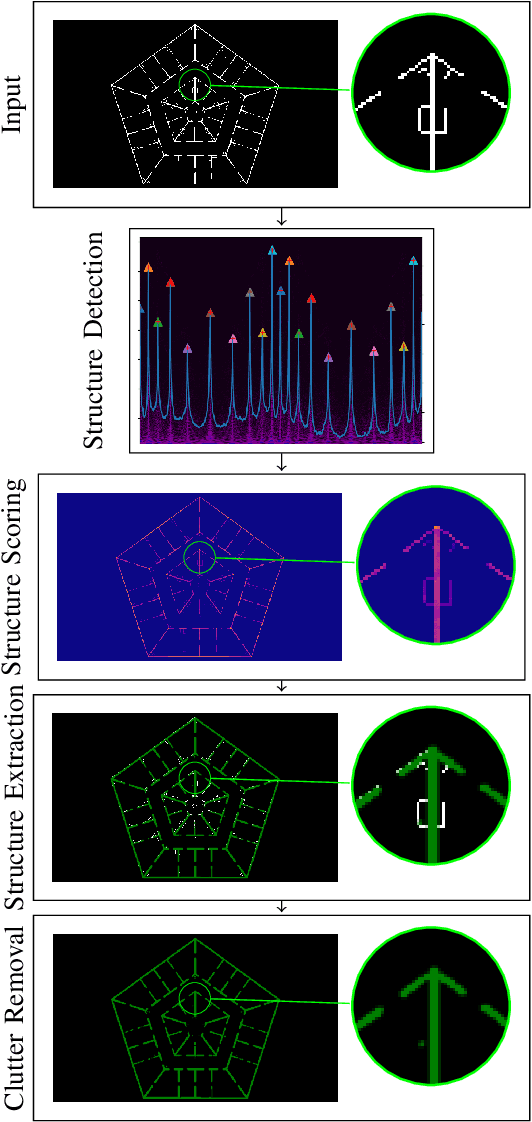
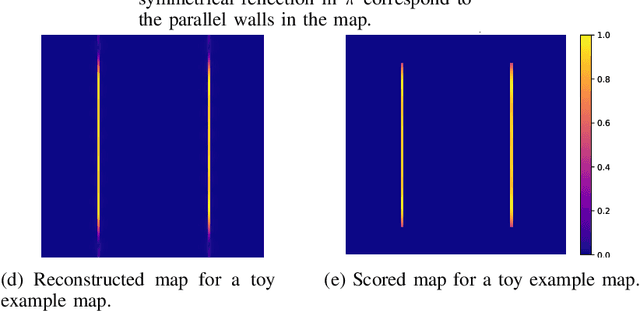
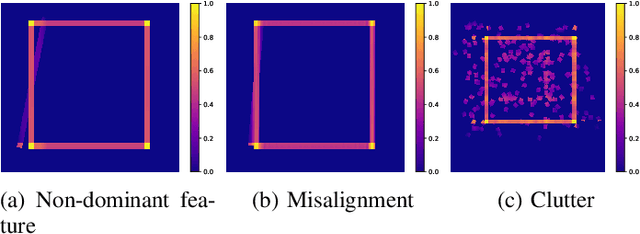
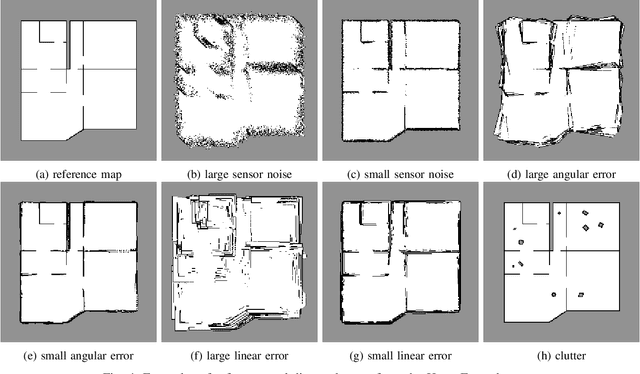
We propose a method for measuring how well each point in an indoor 2D robot map agrees with the underlying structure that governs the construction of the environment. This structure scoring has applications for, e. g., easier robot deployment and Cleaning of maps. In particular, we demonstrate its effectiveness for removing clutter and artifacts from real-world maps, which in turn is an enabler for other map processing components, e. g., room segmentation. Starting from the Fourier transform, we detect peaks in the unfolded frequency spectrum that correspond to a set of dominant directions. This allows us to reconstruct a nominal reference map and score the input map through its correspondence with this reference, without requiring access to a ground-truth map.