Direct Ascent Synthesis: Revealing Hidden Generative Capabilities in Discriminative Models

We demonstrate that discriminative models inherently contain powerful generative capabilities, challenging the fundamental distinction between discriminative and generative architectures. Our method, Direct Ascent Synthesis (DAS), reveals these latent capabilities through multi-resolution optimization of CLIP model representations. While traditional inversion attempts produce adversarial patterns, DAS achieves high-quality image synthesis by decomposing optimization across multiple spatial scales (1x1 to 224x224), requiring no additional training. This approach not only enables diverse applications -- from text-to-image generation to style transfer -- but maintains natural image statistics ($1/f^2$ spectrum) and guides the generation away from non-robust adversarial patterns. Our results demonstrate that standard discriminative models encode substantially richer generative knowledge than previously recognized, providing new perspectives on model interpretability and the relationship between adversarial examples and natural image synthesis.

A Note on Implementation Errors in Recent Adaptive Attacks Against Multi-Resolution Self-Ensembles

This note documents an implementation issue in recent adaptive attacks (Zhang et al. [2024]) against the multi-resolution self-ensemble defense (Fort and Lakshminarayanan [2024]). The implementation allowed adversarial perturbations to exceed the standard $L_\infty = 8/255$ bound by up to a factor of 20$\times$, reaching magnitudes of up to $L_\infty = 160/255$. When attacks are properly constrained within the intended bounds, the defense maintains non-trivial robustness. Beyond highlighting the importance of careful validation in adversarial machine learning research, our analysis reveals an intriguing finding: properly bounded adaptive attacks against strong multi-resolution self-ensembles often align with human perception, suggesting the need to reconsider how we measure adversarial robustness.

Ensemble everything everywhere: Multi-scale aggregation for adversarial robustness

Adversarial examples pose a significant challenge to the robustness, reliability and alignment of deep neural networks. We propose a novel, easy-to-use approach to achieving high-quality representations that lead to adversarial robustness through the use of multi-resolution input representations and dynamic self-ensembling of intermediate layer predictions. We demonstrate that intermediate layer predictions exhibit inherent robustness to adversarial attacks crafted to fool the full classifier, and propose a robust aggregation mechanism based on Vickrey auction that we call \textit{CrossMax} to dynamically ensemble them. By combining multi-resolution inputs and robust ensembling, we achieve significant adversarial robustness on CIFAR-10 and CIFAR-100 datasets without any adversarial training or extra data, reaching an adversarial accuracy of $\approx$72% (CIFAR-10) and $\approx$48% (CIFAR-100) on the RobustBench AutoAttack suite ($L_\infty=8/255)$ with a finetuned ImageNet-pretrained ResNet152. This represents a result comparable with the top three models on CIFAR-10 and a +5 % gain compared to the best current dedicated approach on CIFAR-100. Adding simple adversarial training on top, we get $\approx$78% on CIFAR-10 and $\approx$51% on CIFAR-100, improving SOTA by 5 % and 9 % respectively and seeing greater gains on the harder dataset. We validate our approach through extensive experiments and provide insights into the interplay between adversarial robustness, and the hierarchical nature of deep representations. We show that simple gradient-based attacks against our model lead to human-interpretable images of the target classes as well as interpretable image changes. As a byproduct, using our multi-resolution prior, we turn pre-trained classifiers and CLIP models into controllable image generators and develop successful transferable attacks on large vision language models.

Scaling Laws for Adversarial Attacks on Language Model Activations

We explore a class of adversarial attacks targeting the activations of language models. By manipulating a relatively small subset of model activations, $a$, we demonstrate the ability to control the exact prediction of a significant number (in some cases up to 1000) of subsequent tokens $t$. We empirically verify a scaling law where the maximum number of target tokens $t_\mathrm{max}$ predicted depends linearly on the number of tokens $a$ whose activations the attacker controls as $t_\mathrm{max} = \kappa a$. We find that the number of bits of control in the input space needed to control a single bit in the output space (what we call attack resistance $\chi$) is remarkably constant between $\approx 16$ and $\approx 25$ over 2 orders of magnitude of model sizes for different language models. Compared to attacks on tokens, attacks on activations are predictably much stronger, however, we identify a surprising regularity where one bit of input steered either via activations or via tokens is able to exert control over a similar amount of output bits. This gives support for the hypothesis that adversarial attacks are a consequence of dimensionality mismatch between the input and output spaces. A practical implication of the ease of attacking language model activations instead of tokens is for multi-modal and selected retrieval models, where additional data sources are added as activations directly, sidestepping the tokenized input. This opens up a new, broad attack surface. By using language models as a controllable test-bed to study adversarial attacks, we were able to experiment with input-output dimensions that are inaccessible in computer vision, especially where the output dimension dominates.

Multi-attacks: Many images $+$ the same adversarial attack $\to$ many target labels

We show that we can easily design a single adversarial perturbation $P$ that changes the class of $n$ images $X_1,X_2,\dots,X_n$ from their original, unperturbed classes $c_1, c_2,\dots,c_n$ to desired (not necessarily all the same) classes $c^*_1,c^*_2,\dots,c^*_n$ for up to hundreds of images and target classes at once. We call these \textit{multi-attacks}. Characterizing the maximum $n$ we can achieve under different conditions such as image resolution, we estimate the number of regions of high class confidence around a particular image in the space of pixels to be around $10^{\mathcal{O}(100)}$, posing a significant problem for exhaustive defense strategies. We show several immediate consequences of this: adversarial attacks that change the resulting class based on their intensity, and scale-independent adversarial examples. To demonstrate the redundancy and richness of class decision boundaries in the pixel space, we look for its two-dimensional sections that trace images and spell words using particular classes. We also show that ensembling reduces susceptibility to multi-attacks, and that classifiers trained on random labels are more susceptible. Our code is available on GitHub.

Constitutional AI: Harmlessness from AI Feedback

As AI systems become more capable, we would like to enlist their help to supervise other AIs. We experiment with methods for training a harmless AI assistant through self-improvement, without any human labels identifying harmful outputs. The only human oversight is provided through a list of rules or principles, and so we refer to the method as 'Constitutional AI'. The process involves both a supervised learning and a reinforcement learning phase. In the supervised phase we sample from an initial model, then generate self-critiques and revisions, and then finetune the original model on revised responses. In the RL phase, we sample from the finetuned model, use a model to evaluate which of the two samples is better, and then train a preference model from this dataset of AI preferences. We then train with RL using the preference model as the reward signal, i.e. we use 'RL from AI Feedback' (RLAIF). As a result we are able to train a harmless but non-evasive AI assistant that engages with harmful queries by explaining its objections to them. Both the SL and RL methods can leverage chain-of-thought style reasoning to improve the human-judged performance and transparency of AI decision making. These methods make it possible to control AI behavior more precisely and with far fewer human labels.

Measuring Progress on Scalable Oversight for Large Language Models

Developing safe and useful general-purpose AI systems will require us to make progress on scalable oversight: the problem of supervising systems that potentially outperform us on most skills relevant to the task at hand. Empirical work on this problem is not straightforward, since we do not yet have systems that broadly exceed our abilities. This paper discusses one of the major ways we think about this problem, with a focus on ways it can be studied empirically. We first present an experimental design centered on tasks for which human specialists succeed but unaided humans and current general AI systems fail. We then present a proof-of-concept experiment meant to demonstrate a key feature of this experimental design and show its viability with two question-answering tasks: MMLU and time-limited QuALITY. On these tasks, we find that human participants who interact with an unreliable large-language-model dialog assistant through chat -- a trivial baseline strategy for scalable oversight -- substantially outperform both the model alone and their own unaided performance. These results are an encouraging sign that scalable oversight will be tractable to study with present models and bolster recent findings that large language models can productively assist humans with difficult tasks.

What does a deep neural network confidently perceive? The effective dimension of high certainty class manifolds and their low confidence boundaries

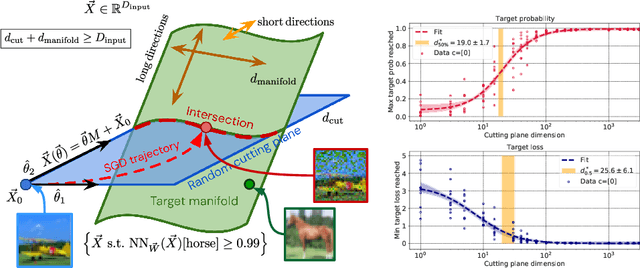
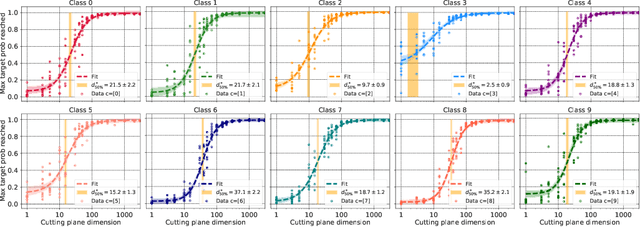
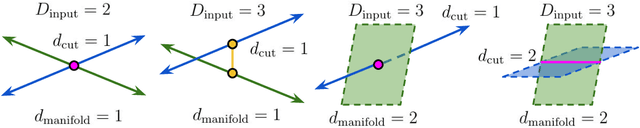
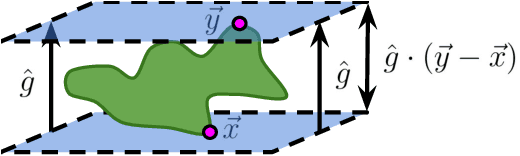
Deep neural network classifiers partition input space into high confidence regions for each class. The geometry of these class manifolds (CMs) is widely studied and intimately related to model performance; for example, the margin depends on CM boundaries. We exploit the notions of Gaussian width and Gordon's escape theorem to tractably estimate the effective dimension of CMs and their boundaries through tomographic intersections with random affine subspaces of varying dimension. We show several connections between the dimension of CMs, generalization, and robustness. In particular we investigate how CM dimension depends on 1) the dataset, 2) architecture (including ResNet, WideResNet \& Vision Transformer), 3) initialization, 4) stage of training, 5) class, 6) network width, 7) ensemble size, 8) label randomization, 9) training set size, and 10) robustness to data corruption. Together a picture emerges that higher performing and more robust models have higher dimensional CMs. Moreover, we offer a new perspective on ensembling via intersections of CMs. Our code is at https://github.com/stanislavfort/slice-dice-optimize/

Language Models (Mostly) Know What They Know

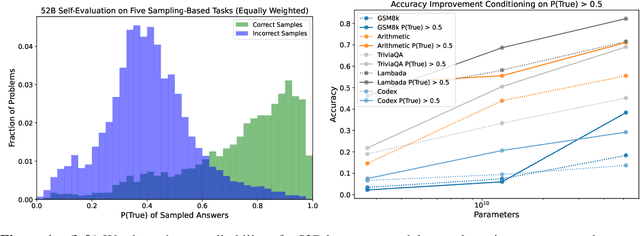
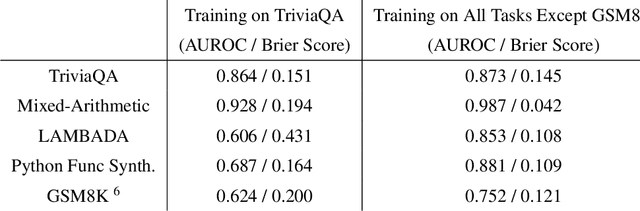
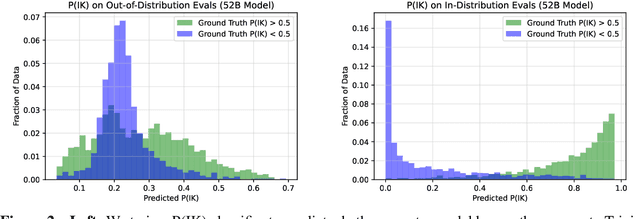
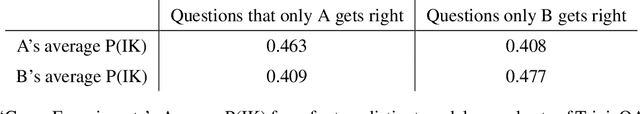
We study whether language models can evaluate the validity of their own claims and predict which questions they will be able to answer correctly. We first show that larger models are well-calibrated on diverse multiple choice and true/false questions when they are provided in the right format. Thus we can approach self-evaluation on open-ended sampling tasks by asking models to first propose answers, and then to evaluate the probability "P(True)" that their answers are correct. We find encouraging performance, calibration, and scaling for P(True) on a diverse array of tasks. Performance at self-evaluation further improves when we allow models to consider many of their own samples before predicting the validity of one specific possibility. Next, we investigate whether models can be trained to predict "P(IK)", the probability that "I know" the answer to a question, without reference to any particular proposed answer. Models perform well at predicting P(IK) and partially generalize across tasks, though they struggle with calibration of P(IK) on new tasks. The predicted P(IK) probabilities also increase appropriately in the presence of relevant source materials in the context, and in the presence of hints towards the solution of mathematical word problems. We hope these observations lay the groundwork for training more honest models, and for investigating how honesty generalizes to cases where models are trained on objectives other than the imitation of human writing.

Training a Helpful and Harmless Assistant with Reinforcement Learning from Human Feedback

We apply preference modeling and reinforcement learning from human feedback (RLHF) to finetune language models to act as helpful and harmless assistants. We find this alignment training improves performance on almost all NLP evaluations, and is fully compatible with training for specialized skills such as python coding and summarization. We explore an iterated online mode of training, where preference models and RL policies are updated on a weekly cadence with fresh human feedback data, efficiently improving our datasets and models. Finally, we investigate the robustness of RLHF training, and identify a roughly linear relation between the RL reward and the square root of the KL divergence between the policy and its initialization. Alongside our main results, we perform peripheral analyses on calibration, competing objectives, and the use of OOD detection, compare our models with human writers, and provide samples from our models using prompts appearing in recent related work.