An efficient nonconvex reformulation of stagewise convex optimization problems

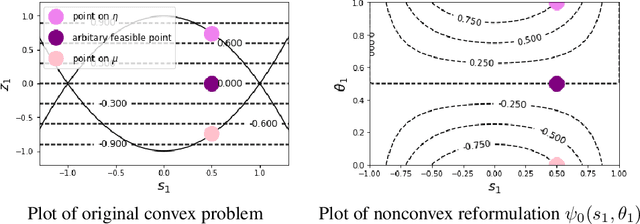
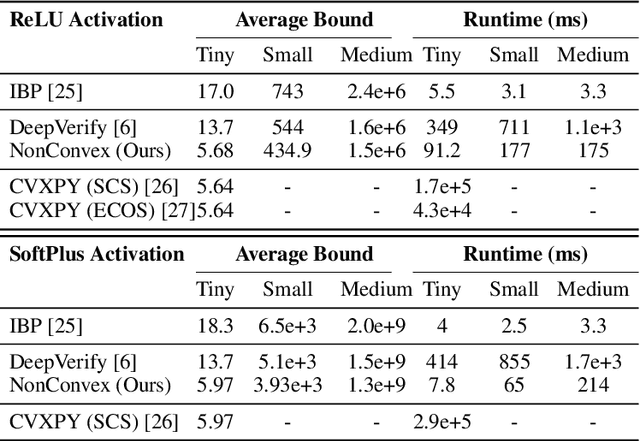
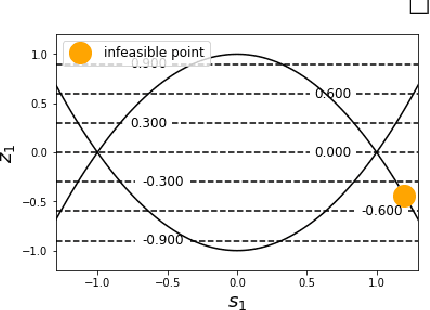
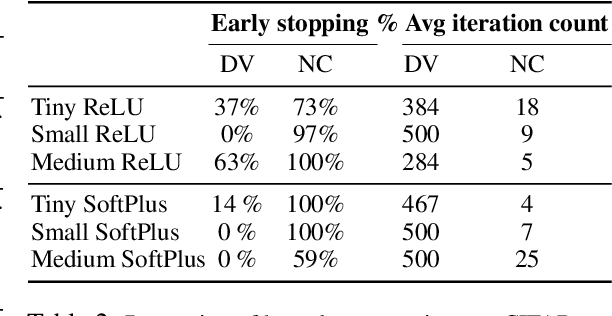
Convex optimization problems with staged structure appear in several contexts, including optimal control, verification of deep neural networks, and isotonic regression. Off-the-shelf solvers can solve these problems but may scale poorly. We develop a nonconvex reformulation designed to exploit this staged structure. Our reformulation has only simple bound constraints, enabling solution via projected gradient methods and their accelerated variants. The method automatically generates a sequence of primal and dual feasible solutions to the original convex problem, making optimality certification easy. We establish theoretical properties of the nonconvex formulation, showing that it is (almost) free of spurious local minima and has the same global optimum as the convex problem. We modify PGD to avoid spurious local minimizers so it always converges to the global minimizer. For neural network verification, our approach obtains small duality gaps in only a few gradient steps. Consequently, it can quickly solve large-scale verification problems faster than both off-the-shelf and specialized solvers.

Coping with Label Shift via Distributionally Robust Optimisation

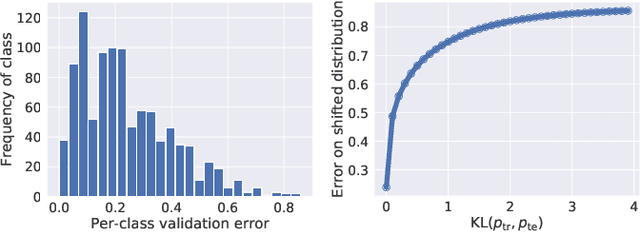
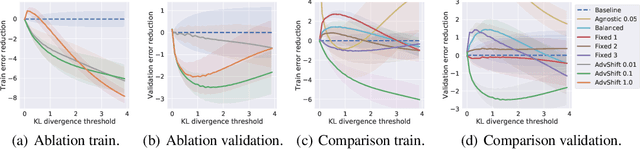
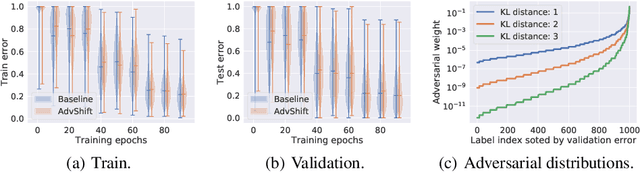
The label shift problem refers to the supervised learning setting where the train and test label distributions do not match. Existing work addressing label shift usually assumes access to an \emph{unlabelled} test sample. This sample may be used to estimate the test label distribution, and to then train a suitably re-weighted classifier. While approaches using this idea have proven effective, their scope is limited as it is not always feasible to access the target domain; further, they require repeated retraining if the model is to be deployed in \emph{multiple} test environments. Can one instead learn a \emph{single} classifier that is robust to arbitrary label shifts from a broad family? In this paper, we answer this question by proposing a model that minimises an objective based on distributionally robust optimisation (DRO). We then design and analyse a gradient descent-proximal mirror ascent algorithm tailored for large-scale problems to optimise the proposed objective. %, and establish its convergence. Finally, through experiments on CIFAR-100 and ImageNet, we show that our technique can significantly improve performance over a number of baselines in settings where label shift is present.

Semantic Label Smoothing for Sequence to Sequence Problems

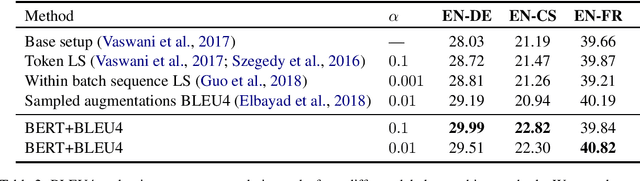
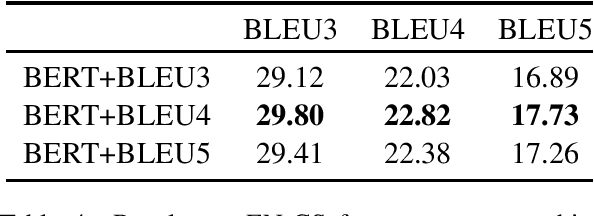
Label smoothing has been shown to be an effective regularization strategy in classification, that prevents overfitting and helps in label de-noising. However, extending such methods directly to seq2seq settings, such as Machine Translation, is challenging: the large target output space of such problems makes it intractable to apply label smoothing over all possible outputs. Most existing approaches for seq2seq settings either do token level smoothing, or smooth over sequences generated by randomly substituting tokens in the target sequence. Unlike these works, in this paper, we propose a technique that smooths over \emph{well formed} relevant sequences that not only have sufficient n-gram overlap with the target sequence, but are also \emph{semantically similar}. Our method shows a consistent and significant improvement over the state-of-the-art techniques on different datasets.

$O(n)$ Connections are Expressive Enough: Universal Approximability of Sparse Transformers

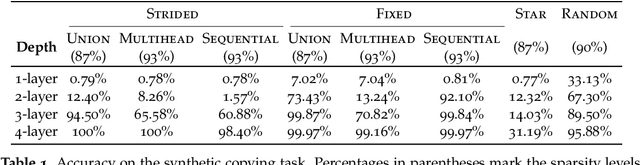
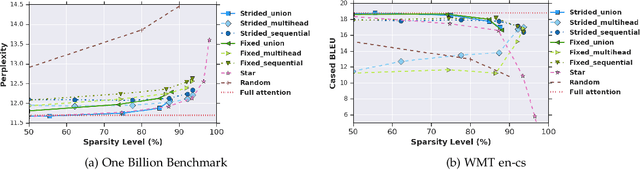
Transformer networks use pairwise attention to compute contextual embeddings of inputs, and have redefined the state of the art in many NLP tasks. However, these models suffer from quadratic computational cost in the input sequence length $n$ to compute attention in each layer. This has prompted recent research into faster attention models, with a predominant approach involving sparsifying the connections in the attention layers. While empirically promising for long sequences, fundamental questions remain unanswered: Can sparse transformers approximate any arbitrary sequence-to-sequence function, similar to their dense counterparts? How does the sparsity pattern and the sparsity level affect their performance? In this paper, we address these questions and provide a unifying framework that captures existing sparse attention models. Our analysis proposes sufficient conditions under which we prove that a sparse attention model can universally approximate any sequence-to-sequence function. Surprisingly, our results show the existence of models with only $O(n)$ connections per attention layer that can approximate the same function class as the dense model with $n^2$ connections. Lastly, we present experiments comparing different patterns/levels of sparsity on standard NLP tasks.

Does label smoothing mitigate label noise?

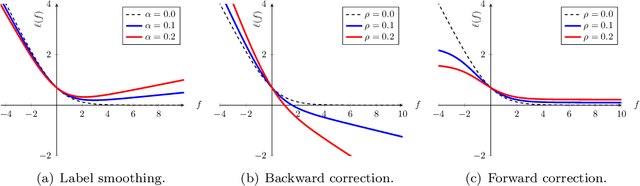
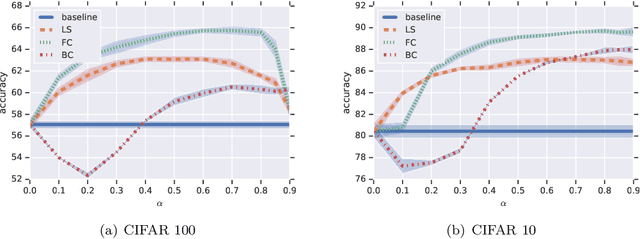
Label smoothing is commonly used in training deep learning models, wherein one-hot training labels are mixed with uniform label vectors. Empirically, smoothing has been shown to improve both predictive performance and model calibration. In this paper, we study whether label smoothing is also effective as a means of coping with label noise. While label smoothing apparently amplifies this problem --- being equivalent to injecting symmetric noise to the labels --- we show how it relates to a general family of loss-correction techniques from the label noise literature. Building on this connection, we show that label smoothing is competitive with loss-correction under label noise. Further, we show that when distilling models from noisy data, label smoothing of the teacher is beneficial; this is in contrast to recent findings for noise-free problems, and sheds further light on settings where label smoothing is beneficial.

Low-Rank Bottleneck in Multi-head Attention Models

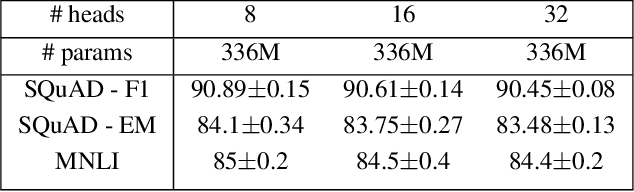
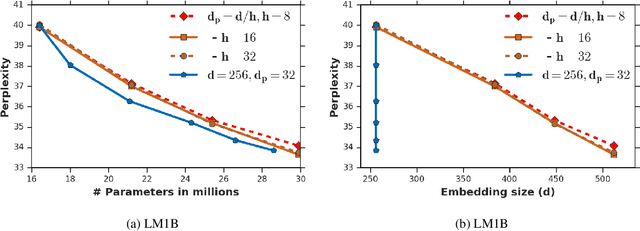
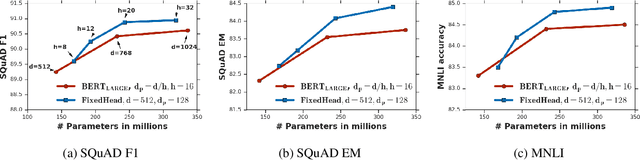
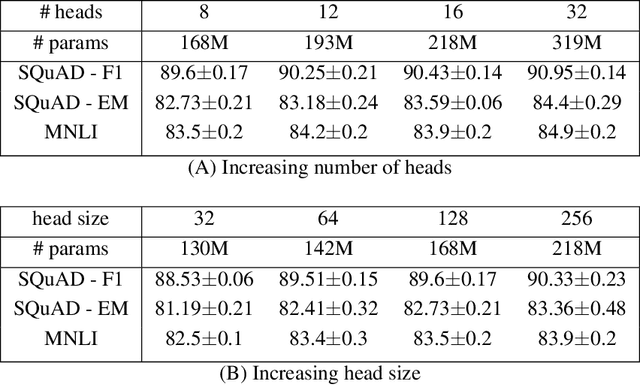
Attention based Transformer architecture has enabled significant advances in the field of natural language processing. In addition to new pre-training techniques, recent improvements crucially rely on working with a relatively larger embedding dimension for tokens. Unfortunately, this leads to models that are prohibitively large to be employed in the downstream tasks. In this paper we identify one of the important factors contributing to the large embedding size requirement. In particular, our analysis highlights that the scaling between the number of heads and the size of each head in the current architecture gives rise to a low-rank bottleneck in attention heads, causing this limitation. We further validate this in our experiments. As a solution we propose to set the head size of an attention unit to input sequence length, and independent of the number of heads, resulting in multi-head attention layers with provably more expressive power. We empirically show that this allows us to train models with a relatively smaller embedding dimension and with better performance scaling.

Are Transformers universal approximators of sequence-to-sequence functions?

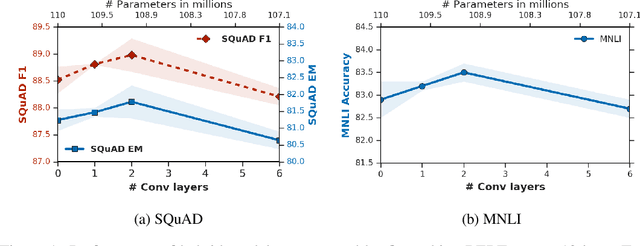
Despite the widespread adoption of Transformer models for NLP tasks, the expressive power of these models is not well-understood. In this paper, we establish that Transformer models are universal approximators of continuous permutation equivariant sequence-to-sequence functions with compact support, which is quite surprising given the amount of shared parameters in these models. Furthermore, using positional encodings, we circumvent the restriction of permutation equivariance, and show that Transformer models can universally approximate arbitrary continuous sequence-to-sequence functions on a compact domain. Interestingly, our proof techniques clearly highlight the different roles of the self-attention and the feed-forward layers in Transformers. In particular, we prove that fixed width self-attention layers can compute contextual mappings of the input sequences, playing a key role in the universal approximation property of Transformers. Based on this insight from our analysis, we consider other simpler alternatives to self-attention layers and empirically evaluate them.

Stabilizing GAN Training with Multiple Random Projections

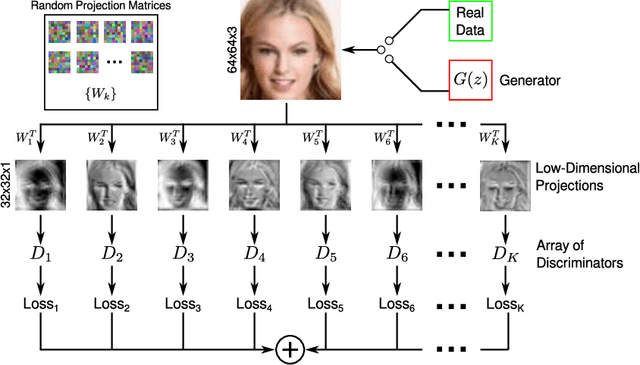
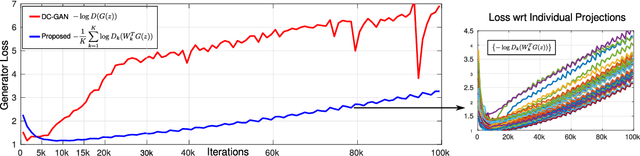
Training generative adversarial networks is unstable in high-dimensions as the true data distribution tends to be concentrated in a small fraction of the ambient space. The discriminator is then quickly able to classify nearly all generated samples as fake, leaving the generator without meaningful gradients and causing it to deteriorate after a point in training. In this work, we propose training a single generator simultaneously against an array of discriminators, each of which looks at a different random low-dimensional projection of the data. Individual discriminators, now provided with restricted views of the input, are unable to reject generated samples perfectly and continue to provide meaningful gradients to the generator throughout training. Meanwhile, the generator learns to produce samples consistent with the full data distribution to satisfy all discriminators simultaneously. We demonstrate the practical utility of this approach experimentally, and show that it is able to produce image samples with higher quality than traditional training with a single discriminator.

Towards Understanding the Role of Over-Parametrization in Generalization of Neural Networks

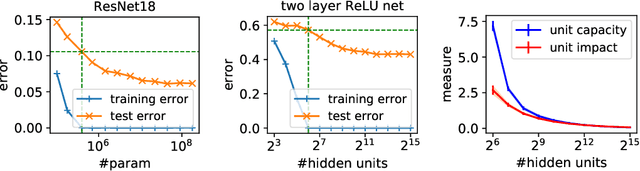
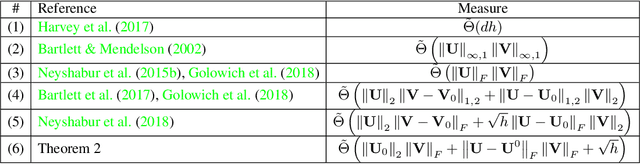
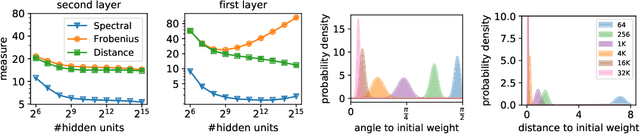
Despite existing work on ensuring generalization of neural networks in terms of scale sensitive complexity measures, such as norms, margin and sharpness, these complexity measures do not offer an explanation of why neural networks generalize better with over-parametrization. In this work we suggest a novel complexity measure based on unit-wise capacities resulting in a tighter generalization bound for two layer ReLU networks. Our capacity bound correlates with the behavior of test error with increasing network sizes, and could potentially explain the improvement in generalization with over-parametrization. We further present a matching lower bound for the Rademacher complexity that improves over previous capacity lower bounds for neural networks.

Smoothed analysis for low-rank solutions to semidefinite programs in quadratic penalty form

Semidefinite programs (SDP) are important in learning and combinatorial optimization with numerous applications. In pursuit of low-rank solutions and low complexity algorithms, we consider the Burer--Monteiro factorization approach for solving SDPs. We show that all approximate local optima are global optima for the penalty formulation of appropriately rank-constrained SDPs as long as the number of constraints scales sub-quadratically with the desired rank of the optimal solution. Our result is based on a simple penalty function formulation of the rank-constrained SDP along with a smoothed analysis to avoid worst-case cost matrices. We particularize our results to two applications, namely, Max-Cut and matrix completion.