A Domain-Agnostic Approach for Characterization of Lifelong Learning Systems

Despite the advancement of machine learning techniques in recent years, state-of-the-art systems lack robustness to "real world" events, where the input distributions and tasks encountered by the deployed systems will not be limited to the original training context, and systems will instead need to adapt to novel distributions and tasks while deployed. This critical gap may be addressed through the development of "Lifelong Learning" systems that are capable of 1) Continuous Learning, 2) Transfer and Adaptation, and 3) Scalability. Unfortunately, efforts to improve these capabilities are typically treated as distinct areas of research that are assessed independently, without regard to the impact of each separate capability on other aspects of the system. We instead propose a holistic approach, using a suite of metrics and an evaluation framework to assess Lifelong Learning in a principled way that is agnostic to specific domains or system techniques. Through five case studies, we show that this suite of metrics can inform the development of varied and complex Lifelong Learning systems. We highlight how the proposed suite of metrics quantifies performance trade-offs present during Lifelong Learning system development - both the widely discussed Stability-Plasticity dilemma and the newly proposed relationship between Sample Efficient and Robust Learning. Further, we make recommendations for the formulation and use of metrics to guide the continuing development of Lifelong Learning systems and assess their progress in the future.

Lifelong Reinforcement Learning with Modulating Masks

Lifelong learning aims to create AI systems that continuously and incrementally learn during a lifetime, similar to biological learning. Attempts so far have met problems, including catastrophic forgetting, interference among tasks, and the inability to exploit previous knowledge. While considerable research has focused on learning multiple input distributions, typically in classification, lifelong reinforcement learning (LRL) must also deal with variations in the state and transition distributions, and in the reward functions. Modulating masks, recently developed for classification, are particularly suitable to deal with such a large spectrum of task variations. In this paper, we adapted modulating masks to work with deep LRL, specifically PPO and IMPALA agents. The comparison with LRL baselines in both discrete and continuous RL tasks shows competitive performance. We further investigated the use of a linear combination of previously learned masks to exploit previous knowledge when learning new tasks: not only is learning faster, the algorithm solves tasks that we could not otherwise solve from scratch due to extremely sparse rewards. The results suggest that RL with modulating masks is a promising approach to lifelong learning, to the composition of knowledge to learn increasingly complex tasks, and to knowledge reuse for efficient and faster learning.

Sliced Optimal Partial Transport

Optimal transport (OT) has become exceedingly popular in machine learning, data science, and computer vision. The core assumption in the OT problem is the equal total amount of mass in source and target measures, which limits its application. Optimal Partial Transport (OPT) is a recently proposed solution to this limitation. Similar to the OT problem, the computation of OPT relies on solving a linear programming problem (often in high dimensions), which can become computationally prohibitive. In this paper, we propose an efficient algorithm for calculating the OPT problem between two non-negative measures in one dimension. Next, following the idea of sliced OT distances, we utilize slicing to define the sliced OPT distance. Finally, we demonstrate the computational and accuracy benefits of the sliced OPT-based method in various numerical experiments. In particular, we show an application of our proposed Sliced-OPT in noisy point cloud registration.

Is Multi-Task Learning an Upper Bound for Continual Learning?

Continual and multi-task learning are common machine learning approaches to learning from multiple tasks. The existing works in the literature often assume multi-task learning as a sensible performance upper bound for various continual learning algorithms. While this assumption is empirically verified for different continual learning benchmarks, it is not rigorously justified. Moreover, it is imaginable that when learning from multiple tasks, a small subset of these tasks could behave as adversarial tasks reducing the overall learning performance in a multi-task setting. In contrast, continual learning approaches can avoid the performance drop caused by such adversarial tasks to preserve their performance on the rest of the tasks, leading to better performance than a multi-task learner. This paper proposes a novel continual self-supervised learning setting, where each task corresponds to learning an invariant representation for a specific class of data augmentations. In this setting, we show that continual learning often beats multi-task learning on various benchmark datasets, including MNIST, CIFAR-10, and CIFAR-100.

Wasserstein Task Embedding for Measuring Task Similarities

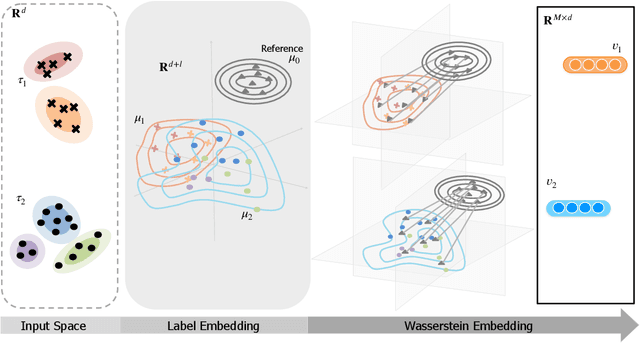
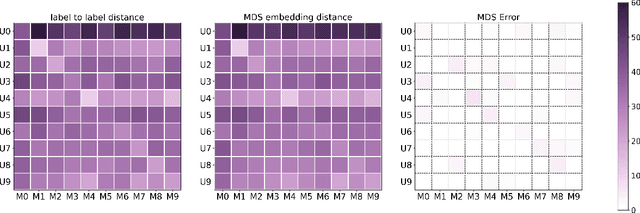
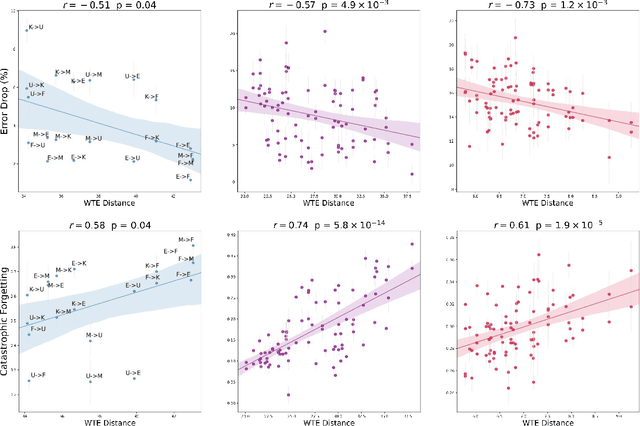
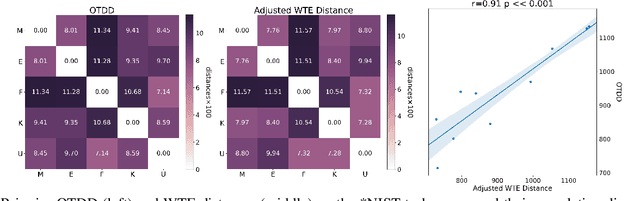
Measuring similarities between different tasks is critical in a broad spectrum of machine learning problems, including transfer, multi-task, continual, and meta-learning. Most current approaches to measuring task similarities are architecture-dependent: 1) relying on pre-trained models, or 2) training networks on tasks and using forward transfer as a proxy for task similarity. In this paper, we leverage the optimal transport theory and define a novel task embedding for supervised classification that is model-agnostic, training-free, and capable of handling (partially) disjoint label sets. In short, given a dataset with ground-truth labels, we perform a label embedding through multi-dimensional scaling and concatenate dataset samples with their corresponding label embeddings. Then, we define the distance between two datasets as the 2-Wasserstein distance between their updated samples. Lastly, we leverage the 2-Wasserstein embedding framework to embed tasks into a vector space in which the Euclidean distance between the embedded points approximates the proposed 2-Wasserstein distance between tasks. We show that the proposed embedding leads to a significantly faster comparison of tasks compared to related approaches like the Optimal Transport Dataset Distance (OTDD). Furthermore, we demonstrate the effectiveness of our proposed embedding through various numerical experiments and show statistically significant correlations between our proposed distance and the forward and backward transfer between tasks.

PRANC: Pseudo RAndom Networks for Compacting deep models

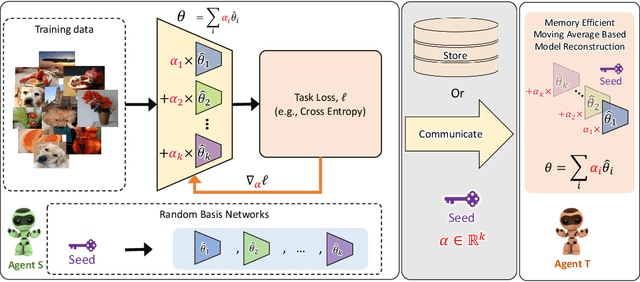
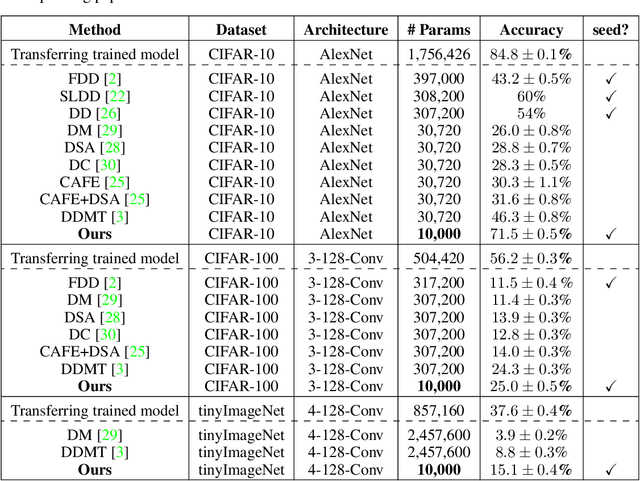
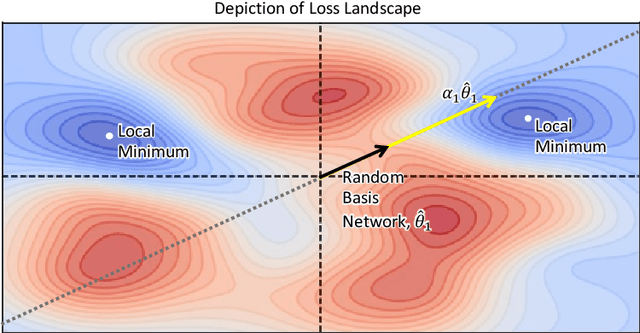
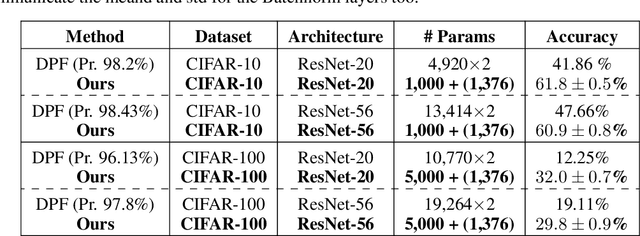
Communication becomes a bottleneck in various distributed Machine Learning settings. Here, we propose a novel training framework that leads to highly efficient communication of models between agents. In short, we train our network to be a linear combination of many pseudo-randomly generated frozen models. For communication, the source agent transmits only the `seed' scalar used to generate the pseudo-random `basis' networks along with the learned linear mixture coefficients. Our method, denoted as PRANC, learns almost $100\times$ fewer parameters than a deep model and still performs well on several datasets and architectures. PRANC enables 1) efficient communication of models between agents, 2) efficient model storage, and 3) accelerated inference by generating layer-wise weights on the fly. We test PRANC on CIFAR-10, CIFAR-100, tinyImageNet, and ImageNet-100 with various architectures like AlexNet, LeNet, ResNet18, ResNet20, and ResNet56 and demonstrate a massive reduction in the number of parameters while providing satisfactory performance on these benchmark datasets. The code is available \href{https://github.com/UCDvision/PRANC}{https://github.com/UCDvision/PRANC}

Sparsity and Heterogeneous Dropout for Continual Learning in the Null Space of Neural Activations

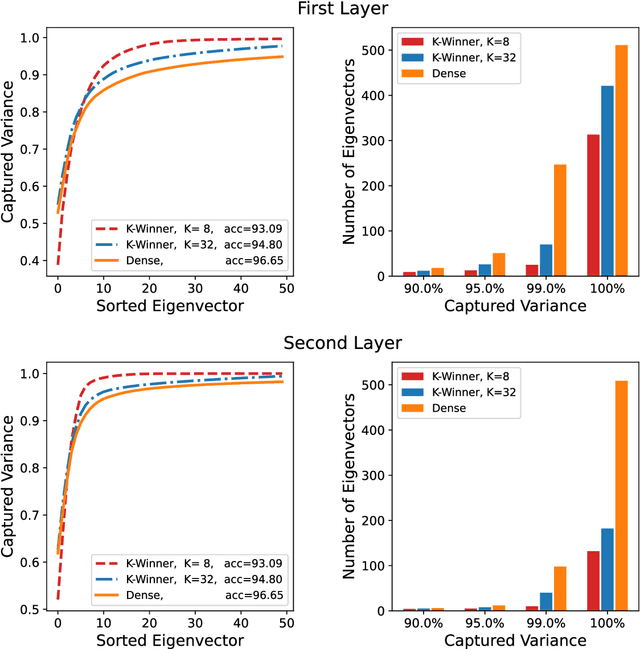
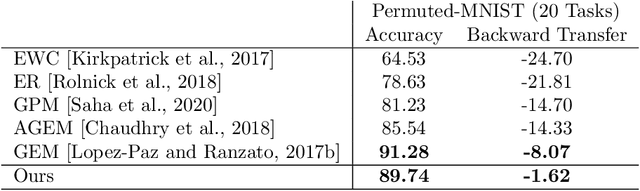
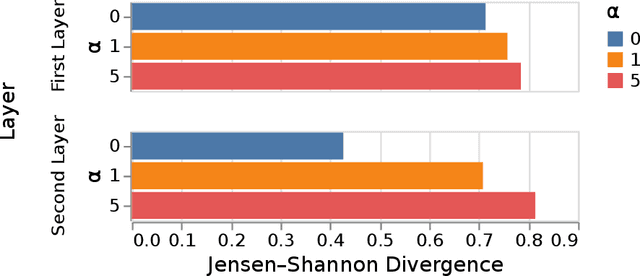
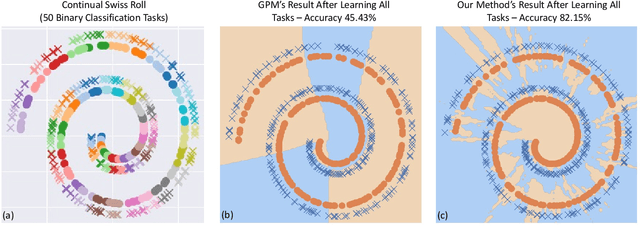
Continual/lifelong learning from a non-stationary input data stream is a cornerstone of intelligence. Despite their phenomenal performance in a wide variety of applications, deep neural networks are prone to forgetting their previously learned information upon learning new ones. This phenomenon is called "catastrophic forgetting" and is deeply rooted in the stability-plasticity dilemma. Overcoming catastrophic forgetting in deep neural networks has become an active field of research in recent years. In particular, gradient projection-based methods have recently shown exceptional performance at overcoming catastrophic forgetting. This paper proposes two biologically-inspired mechanisms based on sparsity and heterogeneous dropout that significantly increase a continual learner's performance over a long sequence of tasks. Our proposed approach builds on the Gradient Projection Memory (GPM) framework. We leverage K-winner activations in each layer of a neural network to enforce layer-wise sparse activations for each task, together with a between-task heterogeneous dropout that encourages the network to use non-overlapping activation patterns between different tasks. In addition, we introduce Continual Swiss Roll as a lightweight and interpretable -- yet challenging -- synthetic benchmark for continual learning. Lastly, we provide an in-depth analysis of our proposed method and demonstrate a significant performance boost on various benchmark continual learning problems.

Teaching Networks to Solve Optimization Problems

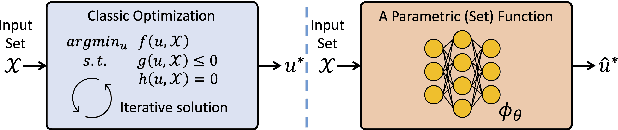
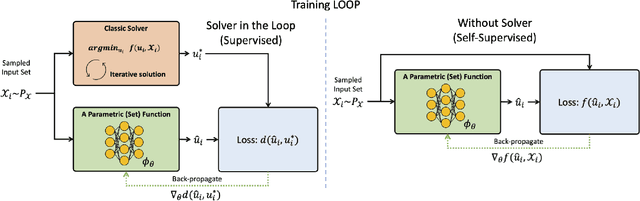
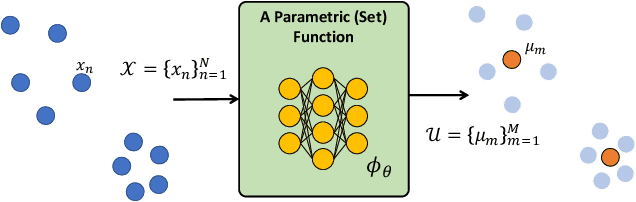
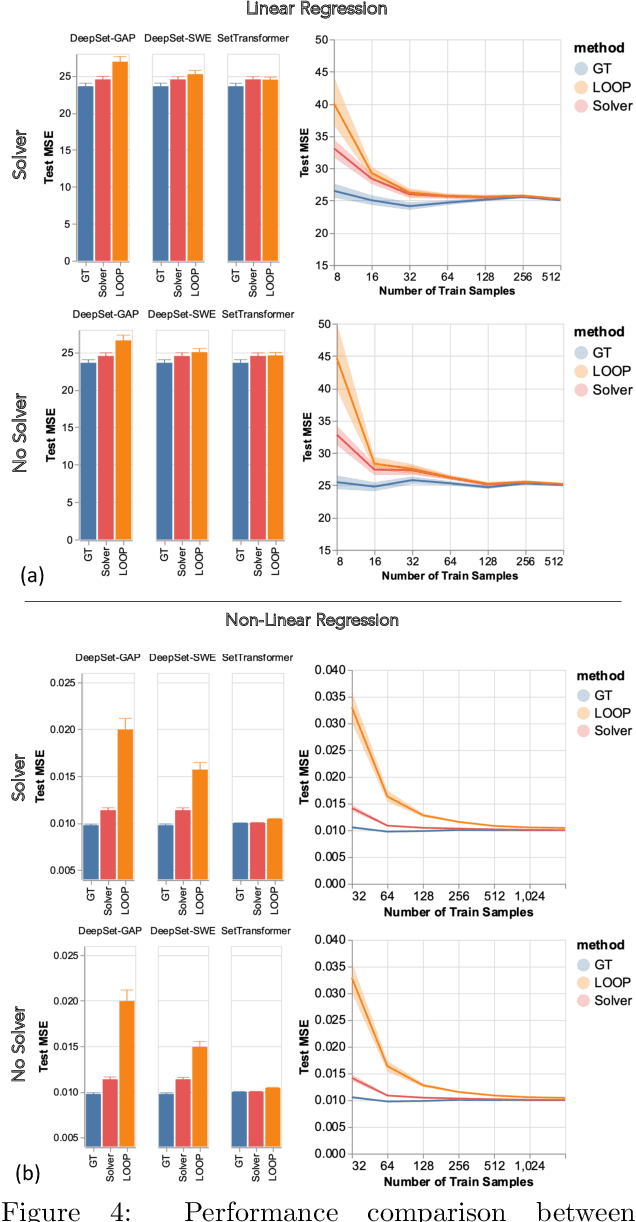
Leveraging machine learning to optimize the optimization process is an emerging field which holds the promise to bypass the fundamental computational bottleneck caused by traditional iterative solvers in critical applications requiring near-real-time optimization. The majority of existing approaches focus on learning data-driven optimizers that lead to fewer iterations in solving an optimization. In this paper, we take a different approach and propose to replace the iterative solvers altogether with a trainable parametric set function that outputs the optimal arguments/parameters of an optimization problem in a single feed-forward. We denote our method as, Learning to Optimize the Optimization Process (LOOP). We show the feasibility of learning such parametric (set) functions to solve various classic optimization problems, including linear/nonlinear regression, principal component analysis, transport-based core-set, and quadratic programming in supply management applications. In addition, we propose two alternative approaches for learning such parametric functions, with and without a solver in the-LOOP. Finally, we demonstrate the effectiveness of our proposed approach through various numerical experiments.

SLOSH: Set LOcality Sensitive Hashing via Sliced-Wasserstein Embeddings

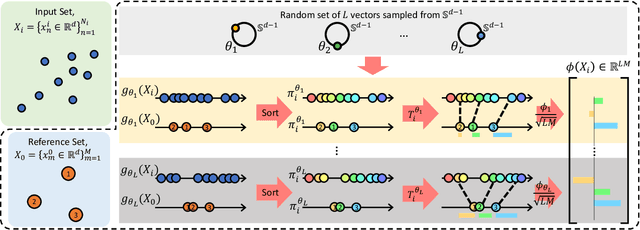
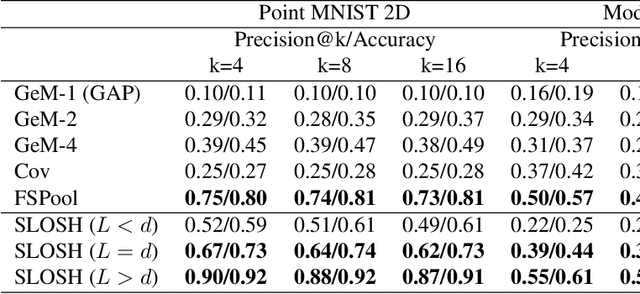
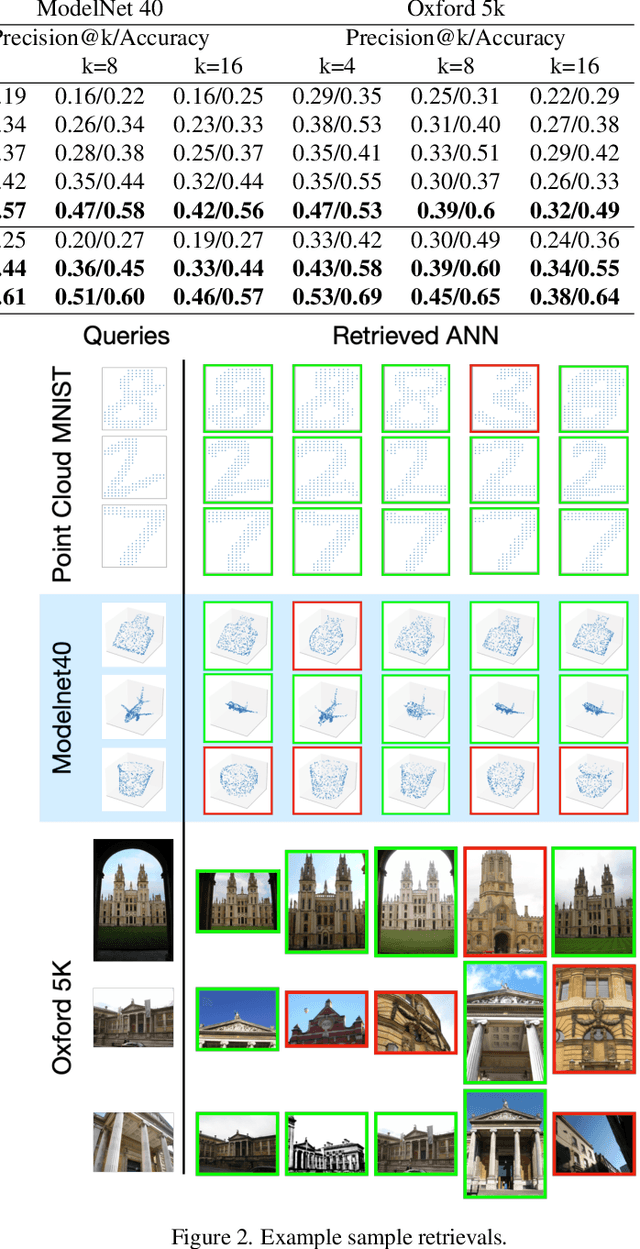
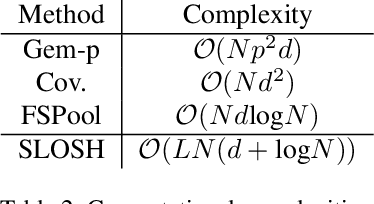
Learning from set-structured data is an essential problem with many applications in machine learning and computer vision. This paper focuses on non-parametric and data-independent learning from set-structured data using approximate nearest neighbor (ANN) solutions, particularly locality-sensitive hashing. We consider the problem of set retrieval from an input set query. Such retrieval problem requires: 1) an efficient mechanism to calculate the distances/dissimilarities between sets, and 2) an appropriate data structure for fast nearest neighbor search. To that end, we propose Sliced-Wasserstein set embedding as a computationally efficient "set-2-vector" mechanism that enables downstream ANN, with theoretical guarantees. The set elements are treated as samples from an unknown underlying distribution, and the Sliced-Wasserstein distance is used to compare sets. We demonstrate the effectiveness of our algorithm, denoted as Set-LOcality Sensitive Hashing (SLOSH), on various set retrieval datasets and compare our proposed embedding with standard set embedding approaches, including Generalized Mean (GeM) embedding/pooling, Featurewise Sort Pooling (FSPool), and Covariance Pooling and show consistent improvement in retrieval results. The code for replicating our results is available here: \href{https://github.com/mint-vu/SLOSH}{https://github.com/mint-vu/SLOSH}.

Lifelong Learning with Sketched Structural Regularization

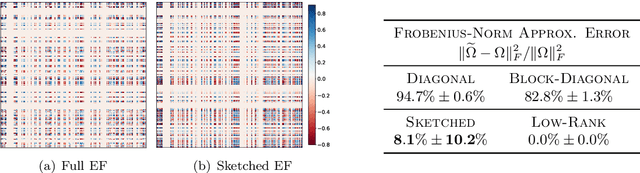
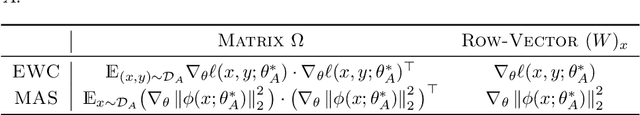
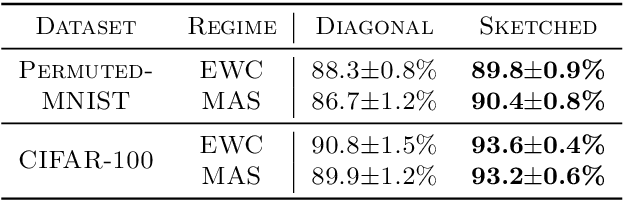
Preventing catastrophic forgetting while continually learning new tasks is an essential problem in lifelong learning. Structural regularization (SR) refers to a family of algorithms that mitigate catastrophic forgetting by penalizing the network for changing its "critical parameters" from previous tasks while learning a new one. The penalty is often induced via a quadratic regularizer defined by an \emph{importance matrix}, e.g., the (empirical) Fisher information matrix in the Elastic Weight Consolidation framework. In practice and due to computational constraints, most SR methods crudely approximate the importance matrix by its diagonal. In this paper, we propose \emph{Sketched Structural Regularization} (Sketched SR) as an alternative approach to compress the importance matrices used for regularizing in SR methods. Specifically, we apply \emph{linear sketching methods} to better approximate the importance matrices in SR algorithms. We show that sketched SR: (i) is computationally efficient and straightforward to implement, (ii) provides an approximation error that is justified in theory, and (iii) is method oblivious by construction and can be adapted to any method that belongs to the structural regularization class. We show that our proposed approach consistently improves various SR algorithms' performance on both synthetic experiments and benchmark continual learning tasks, including permuted-MNIST and CIFAR-100.