An Efficient Transport-Based Dissimilarity Measure for Time Series Classification under Warping Distortions

Time Series Classification (TSC) is an important problem with numerous applications in science and technology. Dissimilarity-based approaches, such as Dynamic Time Warping (DTW), are classical methods for distinguishing time series when time deformations are confounding information. In this paper, starting from a deformation-based model for signal classes we define a problem statement for time series classification problem. We show that, under theoretically ideal conditions, a continuous version of classic 1NN-DTW method can solve the stated problem, even when only one training sample is available. In addition, we propose an alternative dissimilarity measure based on Optimal Transport and show that it can also solve the aforementioned problem statement at a significantly reduced computational cost. Finally, we demonstrate the application of the newly proposed approach in simulated and real time series classification data, showing the efficacy of the method.

LCOT: Linear circular optimal transport

The optimal transport problem for measures supported on non-Euclidean spaces has recently gained ample interest in diverse applications involving representation learning. In this paper, we focus on circular probability measures, i.e., probability measures supported on the unit circle, and introduce a new computationally efficient metric for these measures, denoted as Linear Circular Optimal Transport (LCOT). The proposed metric comes with an explicit linear embedding that allows one to apply Machine Learning (ML) algorithms to the embedded measures and seamlessly modify the underlying metric for the ML algorithm to LCOT. We show that the proposed metric is rooted in the Circular Optimal Transport (COT) and can be considered the linearization of the COT metric with respect to a fixed reference measure. We provide a theoretical analysis of the proposed metric and derive the computational complexities for pairwise comparison of circular probability measures. Lastly, through a set of numerical experiments, we demonstrate the benefits of LCOT in learning representations of circular measures.

System Identification Using the Signed Cumulative Distribution Transform In Structural Health Monitoring Applications

This paper presents a novel, data-driven approach to identifying partial differential equation (PDE) parameters of a dynamical system in structural health monitoring applications. Specifically, we adopt a mathematical "transport" model of the sensor data that allows us to accurately estimate the model parameters, including those associated with structural damage. This is accomplished by means of a newly-developed transform, the signed cumulative distribution transform (SCDT), which is shown to convert the general, nonlinear parameter estimation problem into a simple linear regression. This approach has the additional practical advantage of requiring no a priori knowledge of the source of the excitation (or, alternatively, the initial conditions). By using training sensor data, we devise a coarse regression procedure to recover different PDE parameters from a single sensor measurement. Numerical experiments show that the proposed regression procedure is capable of detecting and estimating PDE parameters with superior accuracy compared to a number of recently developed "Deep Learning" methods. The Python implementation of the proposed system identification technique is integrated as a part of the software package PyTransKit (https://github.com/rohdelab/PyTransKit).

The Radon Signed Cumulative Distribution Transform and its applications in classification of Signed Images

Here we describe a new image representation technique based on the mathematics of transport and optimal transport. The method relies on the combination of the well-known Radon transform for images and a recent signal representation method called the Signed Cumulative Distribution Transform. The newly proposed method generalizes previous transport-related image representation methods to arbitrary functions (images), and thus can be used in more applications. We describe the new transform, and some of its mathematical properties and demonstrate its ability to partition image classes with real and simulated data. In comparison to existing transport transform methods, as well as deep learning-based classification methods, the new transform more accurately represents the information content of signed images, and thus can be used to obtain higher classification accuracies. The implementation of the proposed method in Python language is integrated as a part of the software package PyTransKit, available on Github.

Geodesic Properties of a Generalized Wasserstein Embedding for Time Series Analysis

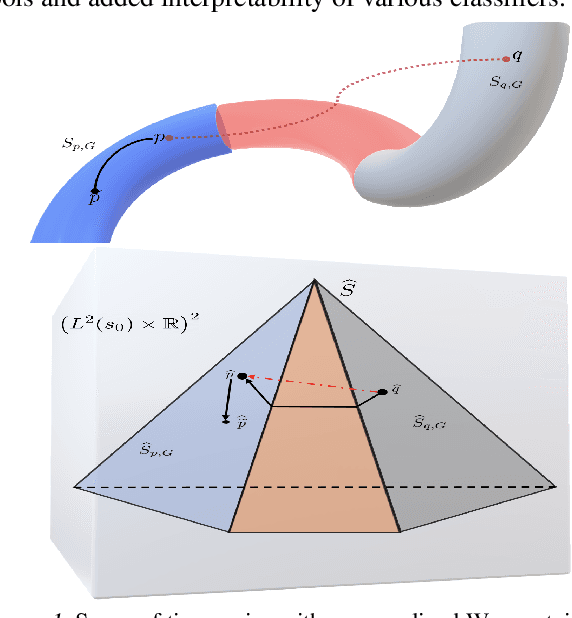
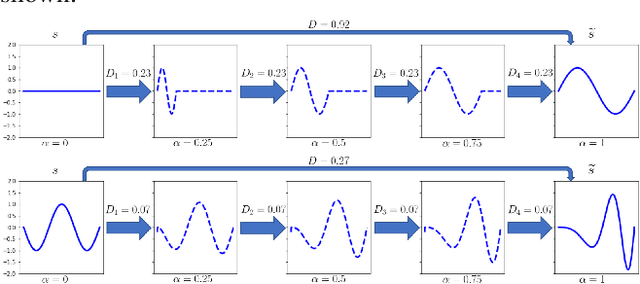
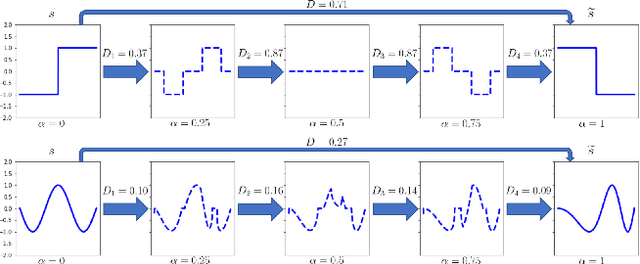
Transport-based metrics and related embeddings (transforms) have recently been used to model signal classes where nonlinear structures or variations are present. In this paper, we study the geodesic properties of time series data with a generalized Wasserstein metric and the geometry related to their signed cumulative distribution transforms in the embedding space. Moreover, we show how understanding such geometric characteristics can provide added interpretability to certain time series classifiers, and be an inspiration for more robust classifiers.

End-to-End Signal Classification in Signed Cumulative Distribution Transform Space

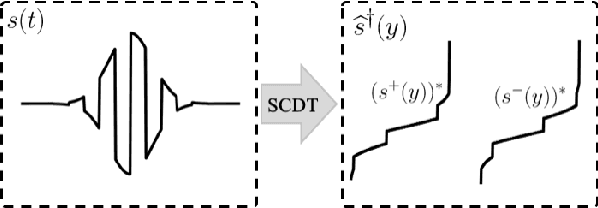
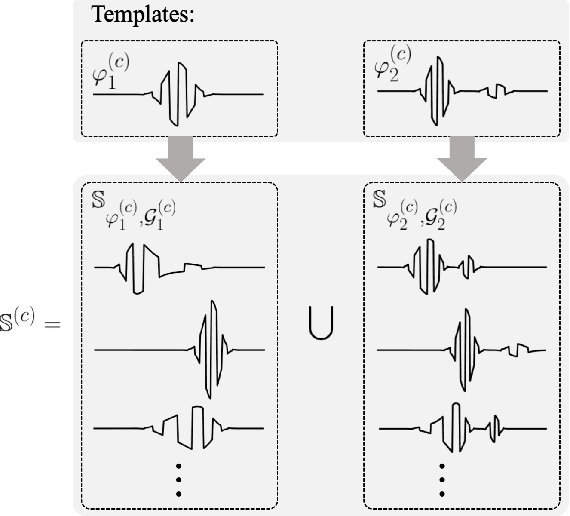
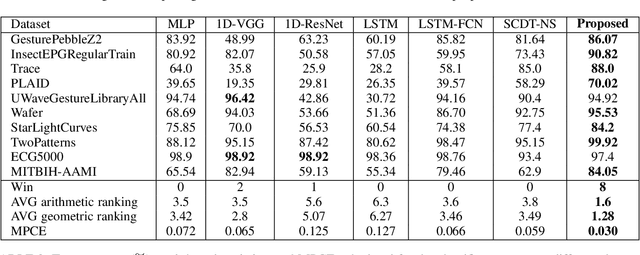
This paper presents a new end-to-end signal classification method using the signed cumulative distribution transform (SCDT). We adopt a transport-based generative model to define the classification problem. We then make use of mathematical properties of the SCDT to render the problem easier in transform domain, and solve for the class of an unknown sample using a nearest local subspace (NLS) search algorithm in SCDT domain. Experiments show that the proposed method provides high accuracy classification results while being data efficient, robust to out-of-distribution samples, and competitive in terms of computational complexity with respect to the deep learning end-to-end classification methods. The implementation of the proposed method in Python language is integrated as a part of the software package PyTransKit (https://github.com/rohdelab/PyTransKit).

Local Sliced-Wasserstein Feature Sets for Illumination-invariant Face Recognition

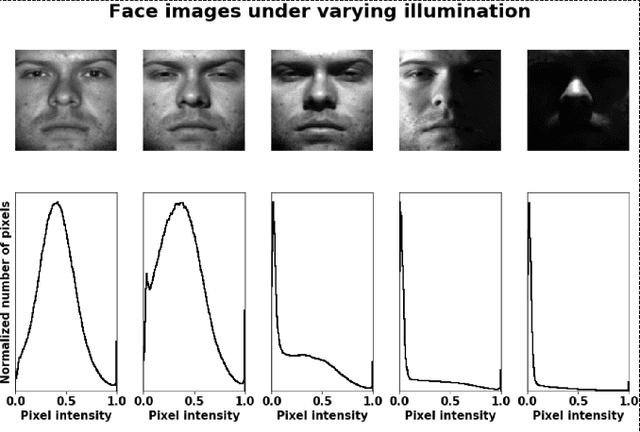
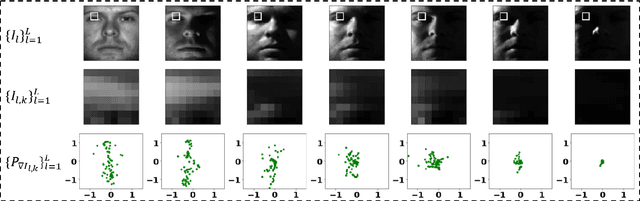
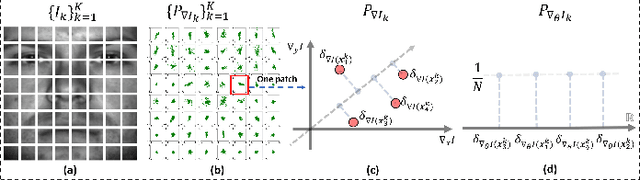
We present a new method for face recognition from digital images acquired under varying illumination conditions. The method is based on mathematical modeling of local gradient distributions using the Radon Cumulative Distribution Transform (R-CDT). We demonstrate that lighting variations cause certain types of deformations of local image gradient distributions which, when expressed in R-CDT domain, can be modeled as a subspace. Face recognition is then performed using a nearest subspace in R-CDT domain of local gradient distributions. Experiment results demonstrate the proposed method outperforms other alternatives in several face recognition tasks with challenging illumination conditions. Python code implementing the proposed method is available, which is integrated as a part of the software package PyTransKit.

Invariance encoding in sliced-Wasserstein space for image classification with limited training data

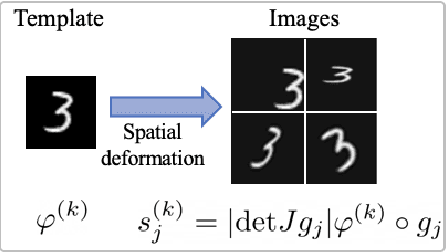
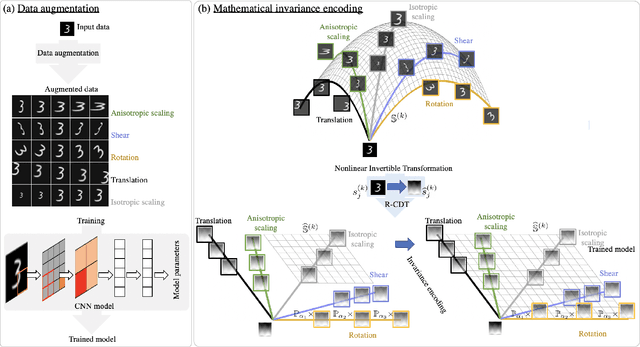
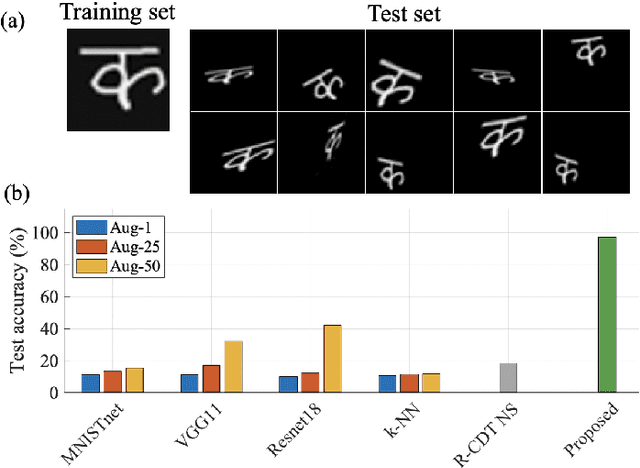
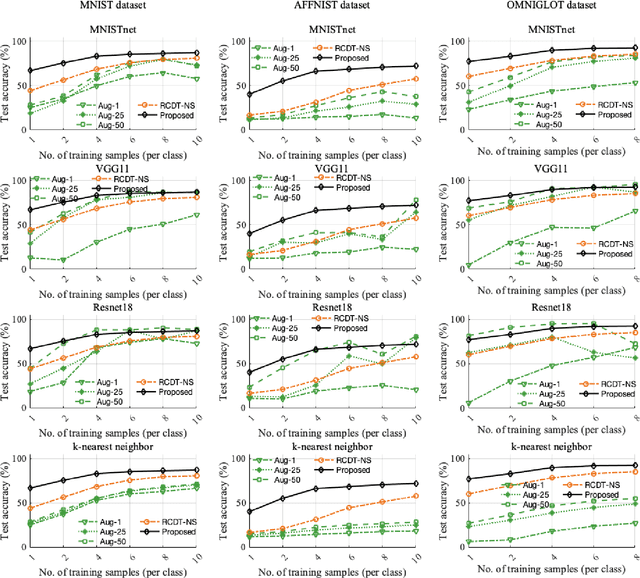
Deep convolutional neural networks (CNNs) are broadly considered to be state-of-the-art generic end-to-end image classification systems. However, they are known to underperform when training data are limited and thus require data augmentation strategies that render the method computationally expensive and not always effective. Rather than using a data augmentation strategy to encode invariances as typically done in machine learning, here we propose to mathematically augment a nearest subspace classification model in sliced-Wasserstein space by exploiting certain mathematical properties of the Radon Cumulative Distribution Transform (R-CDT), a recently introduced image transform. We demonstrate that for a particular type of learning problem, our mathematical solution has advantages over data augmentation with deep CNNs in terms of classification accuracy and computational complexity, and is particularly effective under a limited training data setting. The method is simple, effective, computationally efficient, non-iterative, and requires no parameters to be tuned. Python code implementing our method is available at https://github.com/rohdelab/mathematical_augmentation. Our method is integrated as a part of the software package PyTransKit, which is available at https://github.com/rohdelab/PyTransKit.

Nearest Subspace Search in The Signed Cumulative Distribution Transform Space for 1D Signal Classification

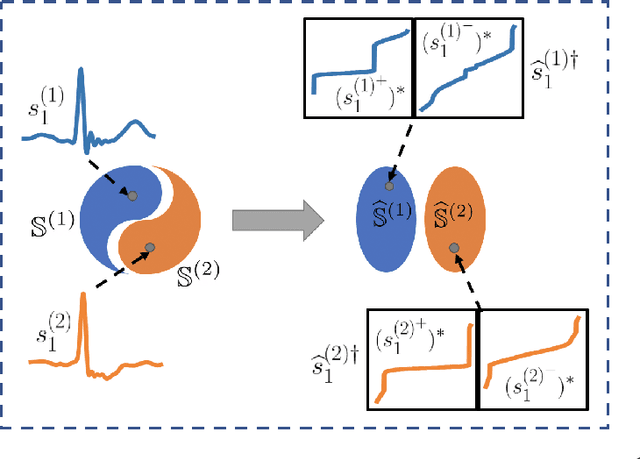
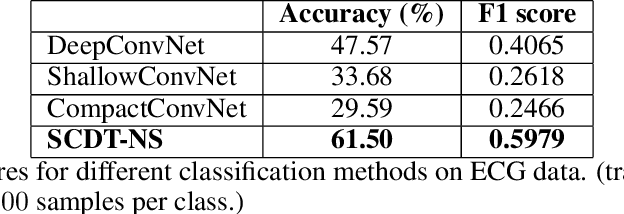
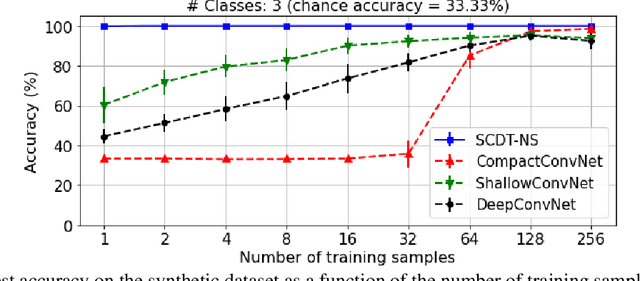
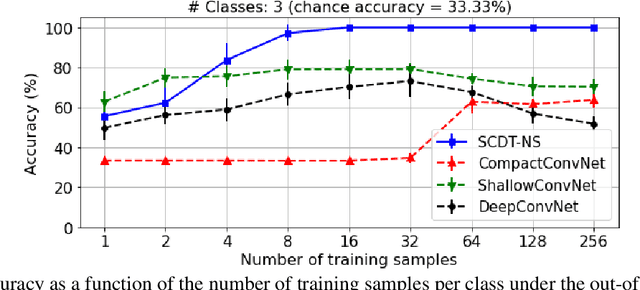
This paper presents a new method to classify 1D signals using the signed cumulative distribution transform (SCDT). The proposed method exploits certain linearization properties of the SCDT to render the problem easier to solve in the SCDT space. The method uses the nearest subspace search technique in the SCDT domain to provide a non-iterative, effective, and simple to implement classification algorithm. Experiments show that the proposed technique outperforms the state-of-the-art neural networks using a very low number of training samples and is also robust to out-of-distribution examples on simulated data. We also demonstrate the efficacy of the proposed technique in real-world applications by applying it to an ECG classification problem. The python code implementing the proposed classifier can be found in PyTransKit (https://github.com/rohdelab/PyTransKit).

The Signed Cumulative Distribution Transform for 1-D Signal Analysis and Classification

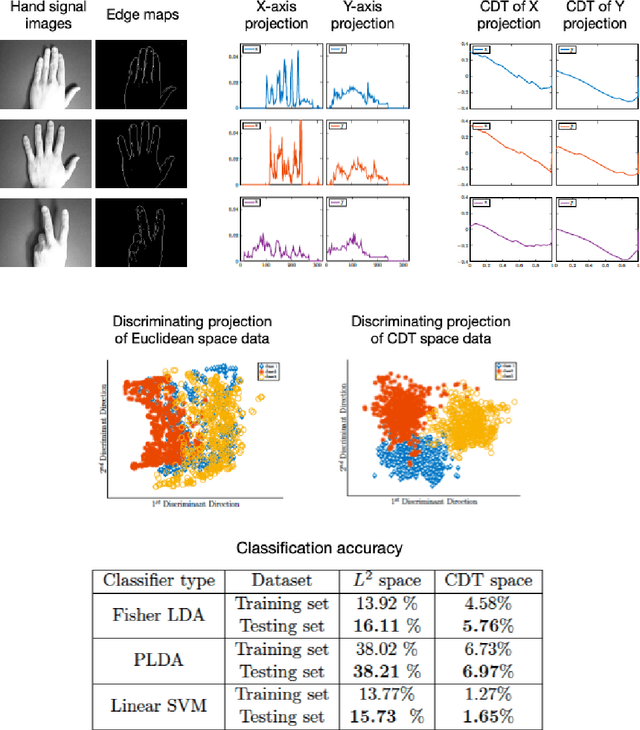
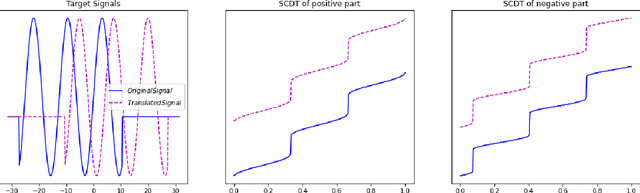
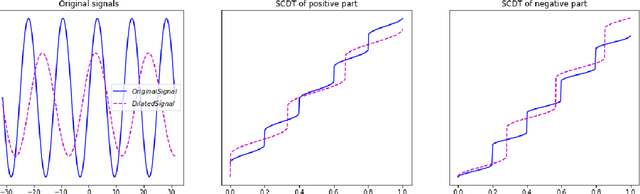
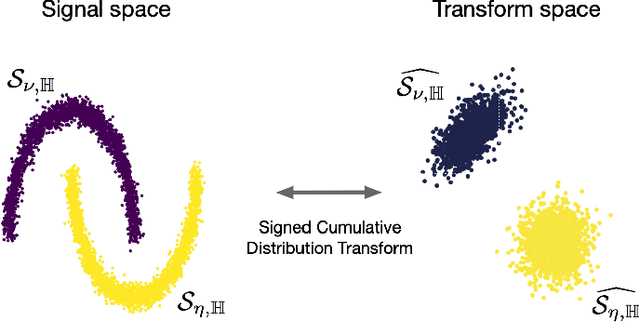
This paper presents a new mathematical signal transform that is especially suitable for decoding information related to non-rigid signal displacements. We provide a measure theoretic framework to extend the existing Cumulative Distribution Transform [ACHA 45 (2018), no. 3, 616-641] to arbitrary (signed) signals on $\overline{\mathbb{R}}$. We present both forward (analysis) and inverse (synthesis) formulas for the transform, and describe several of its properties including translation, scaling, convexity, linear separability and others. Finally, we describe a metric in transform space, and demonstrate the application of the transform in classifying (detecting) signals under random displacements.