BayPrAnoMeta: Bayesian Proto-MAML for Few-Shot Industrial Image Anomaly Detection

Industrial image anomaly detection is a challenging problem owing to extreme class imbalance and the scarcity of labeled defective samples, particularly in few-shot settings. We propose BayPrAnoMeta, a Bayesian generalization of Proto-MAML for few-shot industrial image anomaly detection. Unlike existing Proto-MAML approaches that rely on deterministic class prototypes and distance-based adaptation, BayPrAnoMeta replaces prototypes with task-specific probabilistic normality models and performs inner-loop adaptation via a Bayesian posterior predictive likelihood. We model normal support embeddings with a Normal-Inverse-Wishart (NIW) prior, producing a Student-$t$ predictive distribution that enables uncertainty-aware, heavy-tailed anomaly scoring and is essential for robustness in extreme few-shot settings. We further extend BayPrAnoMeta to a federated meta-learning framework with supervised contrastive regularization for heterogeneous industrial clients and prove convergence to stationary points of the resulting nonconvex objective. Experiments on the MVTec AD benchmark demonstrate consistent and significant AUROC improvements over MAML, Proto-MAML, and PatchCore-based methods in few-shot anomaly detection settings.

Deep learning estimation of the spectral density of functional time series on large domains

We derive an estimator of the spectral density of a functional time series that is the output of a multilayer perceptron neural network. The estimator is motivated by difficulties with the computation of existing spectral density estimators for time series of functions defined on very large grids that arise, for example, in climate compute models and medical scans. Existing estimators use autocovariance kernels represented as large $G \times G$ matrices, where $G$ is the number of grid points on which the functions are evaluated. In many recent applications, functions are defined on 2D and 3D domains, and $G$ can be of the order $G \sim 10^5$, making the evaluation of the autocovariance kernels computationally intensive or even impossible. We use the theory of spectral functional principal components to derive our deep learning estimator and prove that it is a universal approximator to the spectral density under general assumptions. Our estimator can be trained without computing the autocovariance kernels and it can be parallelized to provide the estimates much faster than existing approaches. We validate its performance by simulations and an application to fMRI images.

A Review of Statistical and Machine Learning Approaches for Coral Bleaching Assessment

Coral bleaching is a major concern for marine ecosystems; more than half of the world's coral reefs have either bleached or died over the past three decades. Increasing sea surface temperatures, along with various spatiotemporal environmental factors, are considered the primary reasons behind coral bleaching. The statistical and machine learning communities have focused on multiple aspects of the environment in detail. However, the literature on various stochastic modeling approaches for assessing coral bleaching is extremely scarce. Data-driven strategies are crucial for effective reef management, and this review article provides an overview of existing statistical and machine learning methods for assessing coral bleaching. Statistical frameworks, including simple regression models, generalized linear models, generalized additive models, Bayesian regression models, spatiotemporal models, and resilience indicators, such as Fisher's Information and Variance Index, are commonly used to explore how different environmental stressors influence coral bleaching. On the other hand, machine learning methods, including random forests, decision trees, support vector machines, and spatial operators, are more popular for detecting nonlinear relationships, analyzing high-dimensional data, and allowing integration of heterogeneous data from diverse sources. In addition to summarizing these models, we also discuss potential data-driven future research directions, with a focus on constructing statistical and machine learning models in specific contexts related to coral bleaching.

Classification Using Global and Local Mahalanobis Distances

We propose a novel semi-parametric classifier based on Mahalanobis distances of an observation from the competing classes. Our tool is a generalized additive model with the logistic link function that uses these distances as features to estimate the posterior probabilities of the different classes. While popular parametric classifiers like linear and quadratic discriminant analyses are mainly motivated by the normality of the underlying distributions, the proposed classifier is more flexible and free from such parametric assumptions. Since the densities of elliptic distributions are functions of Mahalanobis distances, this classifier works well when the competing classes are (nearly) elliptic. In such cases, it often outperforms popular nonparametric classifiers, especially when the sample size is small compared to the dimension of the data. To cope with non-elliptic and possibly multimodal distributions, we propose a local version of the Mahalanobis distance. Subsequently, we propose another classifier based on a generalized additive model that uses the local Mahalanobis distances as features. This nonparametric classifier usually performs like the Mahalanobis distance based semiparametric classifier when the underlying distributions are elliptic, but outperforms it for several non-elliptic and multimodal distributions. We also investigate the behaviour of these two classifiers in high dimension, low sample size situations. A thorough numerical study involving several simulated and real datasets demonstrate the usefulness of the proposed classifiers in comparison to many state-of-the-art methods.

CovNet: Covariance Networks for Functional Data on Multidimensional Domains

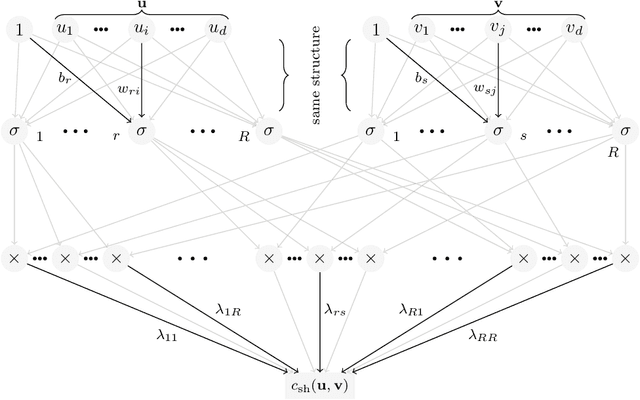
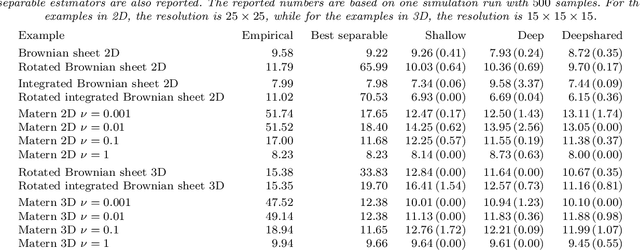
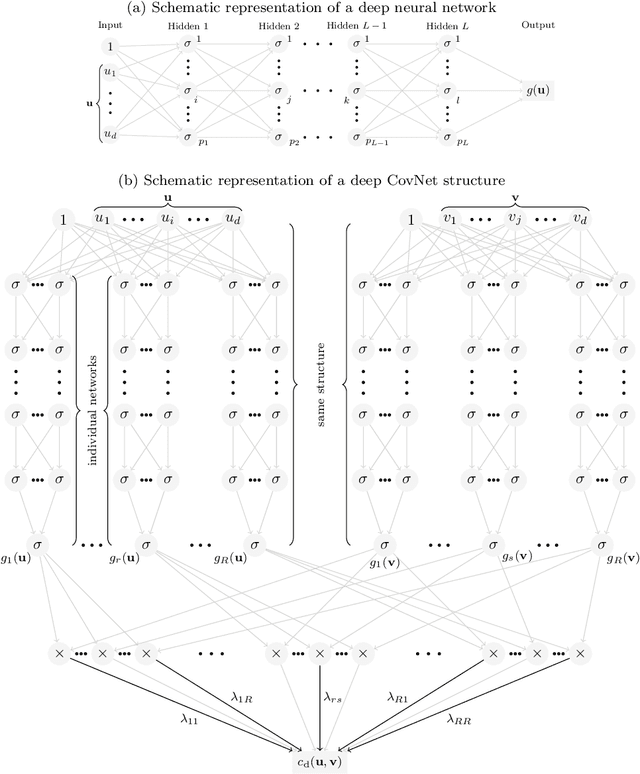
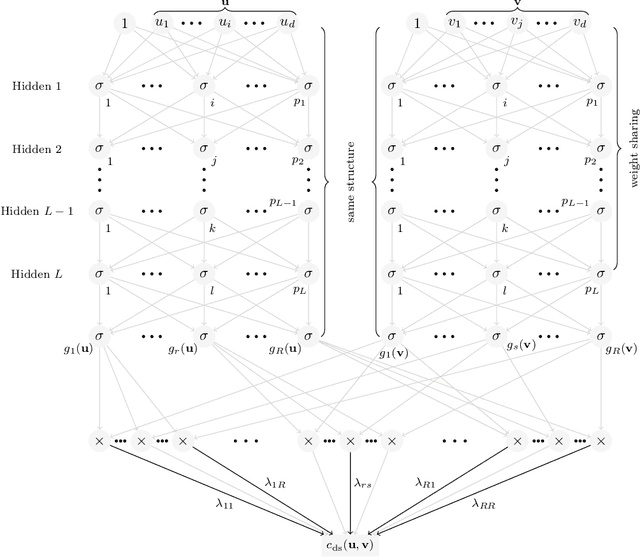
Covariance estimation is ubiquitous in functional data analysis. Yet, the case of functional observations over multidimensional domains introduces computational and statistical challenges, rendering the standard methods effectively inapplicable. To address this problem, we introduce Covariance Networks (CovNet) as a modeling and estimation tool. The CovNet model is universal -- it can be used to approximate any covariance up to desired precision. Moreover, the model can be fitted efficiently to the data and its neural network architecture allows us to employ modern computational tools in the implementation. The CovNet model also admits a closed-form eigen-decomposition, which can be computed efficiently, without constructing the covariance itself. This facilitates easy storage and subsequent manipulation in the context of the CovNet. Moreover, we establish consistency of the proposed estimator and derive its rate of convergence. The usefulness of the proposed method is demonstrated by means of an extensive simulation study.

On a Generalization of the Average Distance Classifier

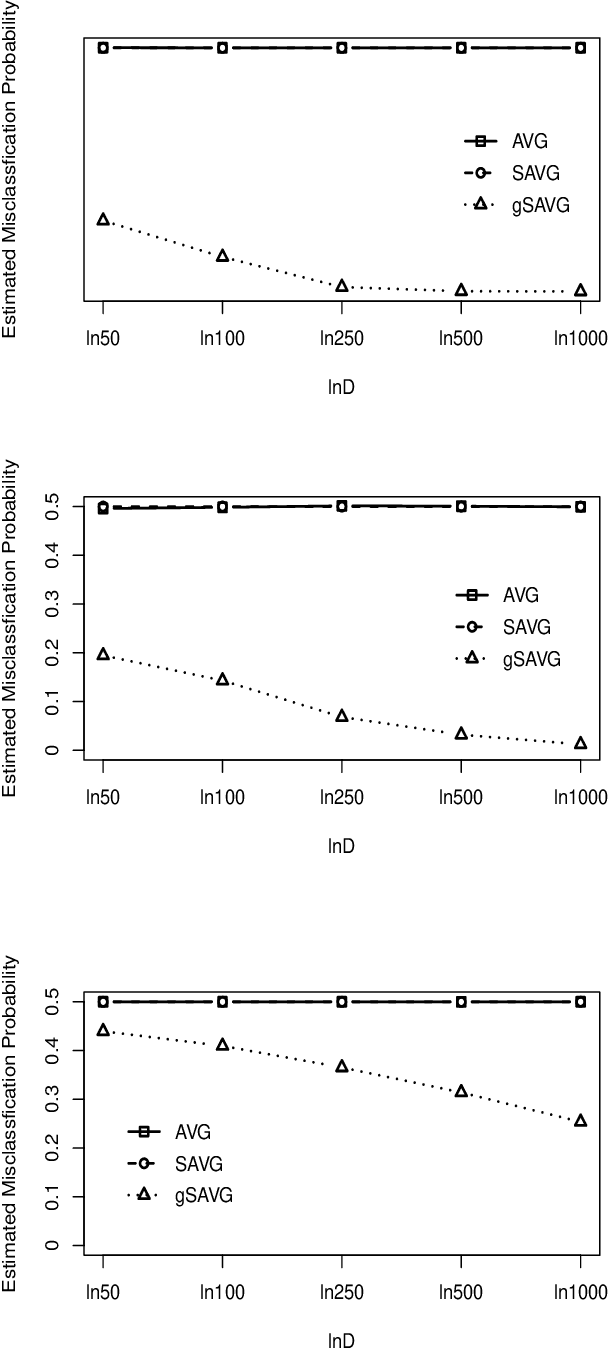
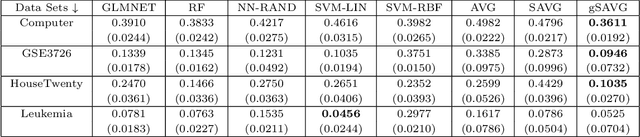
In high dimension, low sample size (HDLSS)settings, the simple average distance classifier based on the Euclidean distance performs poorly if differences between the locations get masked by the scale differences. To rectify this issue, modifications to the average distance classifier was proposed by Chan and Hall (2009). However, the existing classifiers cannot discriminate when the populations differ in other aspects than locations and scales. In this article, we propose some simple transformations of the average distance classifier to tackle this issue. The resulting classifiers perform quite well even when the underlying populations have the same location and scale. The high-dimensional behaviour of the proposed classifiers is studied theoretically. Numerical experiments with a variety of simulated as well as real data sets exhibit the usefulness of the proposed methodology.