An Atmospheric Correction Integrated LULC Segmentation Model for High-Resolution Satellite Imagery

The integration of fine-scale multispectral imagery with deep learning models has revolutionized land use and land cover (LULC) classification. However, the atmospheric effects present in Top-of-Atmosphere sensor measured Digital Number values must be corrected to retrieve accurate Bottom-of-Atmosphere surface reflectance for reliable analysis. This study employs look-up-table-based radiative transfer simulations to estimate the atmospheric path reflectance and transmittance for atmospherically correcting high-resolution CARTOSAT-3 Multispectral (MX) imagery for several Indian cities. The corrected surface reflectance data were subsequently used in supervised and semi-supervised segmentation models, demonstrating stability in multi-class (buildings, roads, trees and water bodies) LULC segmentation accuracy, particularly in scenarios with sparsely labelled data.

D-GRIL: End-to-End Topological Learning with 2-parameter Persistence

End-to-end topological learning using 1-parameter persistence is well-known. We show that the framework can be enhanced using 2-parameter persistence by adopting a recently introduced 2-parameter persistence based vectorization technique called GRIL. We establish a theoretical foundation of differentiating GRIL producing D-GRIL. We show that D-GRIL can be used to learn a bifiltration function on standard benchmark graph datasets. Further, we exhibit that this framework can be applied in the context of bio-activity prediction in drug discovery.

GEFL: Extended Filtration Learning for Graph Classification

Extended persistence is a technique from topological data analysis to obtain global multiscale topological information from a graph. This includes information about connected components and cycles that are captured by the so-called persistence barcodes. We introduce extended persistence into a supervised learning framework for graph classification. Global topological information, in the form of a barcode with four different types of bars and their explicit cycle representatives, is combined into the model by the readout function which is computed by extended persistence. The entire model is end-to-end differentiable. We use a link-cut tree data structure and parallelism to lower the complexity of computing extended persistence, obtaining a speedup of more than 60x over the state-of-the-art for extended persistence computation. This makes extended persistence feasible for machine learning. We show that, under certain conditions, extended persistence surpasses both the WL[1] graph isomorphism test and 0-dimensional barcodes in terms of expressivity because it adds more global (topological) information. In particular, arbitrarily long cycles can be represented, which is difficult for finite receptive field message passing graph neural networks. Furthermore, we show the effectiveness of our method on real world datasets compared to many existing recent graph representation learning methods.

TopoX: A Suite of Python Packages for Machine Learning on Topological Domains

We introduce topox, a Python software suite that provides reliable and user-friendly building blocks for computing and machine learning on topological domains that extend graphs: hypergraphs, simplicial, cellular, path and combinatorial complexes. topox consists of three packages: toponetx facilitates constructing and computing on these domains, including working with nodes, edges and higher-order cells; topoembedx provides methods to embed topological domains into vector spaces, akin to popular graph-based embedding algorithms such as node2vec; topomodelx is built on top of PyTorch and offers a comprehensive toolbox of higher-order message passing functions for neural networks on topological domains. The extensively documented and unit-tested source code of topox is available under MIT license at https://github.com/pyt-team.

ICML 2023 Topological Deep Learning Challenge : Design and Results

This paper presents the computational challenge on topological deep learning that was hosted within the ICML 2023 Workshop on Topology and Geometry in Machine Learning. The competition asked participants to provide open-source implementations of topological neural networks from the literature by contributing to the python packages TopoNetX (data processing) and TopoModelX (deep learning). The challenge attracted twenty-eight qualifying submissions in its two-month duration. This paper describes the design of the challenge and summarizes its main findings.

GRIL: A $2$-parameter Persistence Based Vectorization for Machine Learning

$1$-parameter persistent homology, a cornerstone in Topological Data Analysis (TDA), studies the evolution of topological features such as connected components and cycles hidden in data. It has been applied to enhance the representation power of deep learning models, such as Graph Neural Networks (GNNs). To enrich the representations of topological features, here we propose to study $2$-parameter persistence modules induced by bi-filtration functions. In order to incorporate these representations into machine learning models, we introduce a novel vector representation called Generalized Rank Invariant Landscape \textsc{Gril} for $2$-parameter persistence modules. We show that this vector representation is $1$-Lipschitz stable and differentiable with respect to underlying filtration functions and can be easily integrated into machine learning models to augment encoding topological features. We present an algorithm to compute the vector representation efficiently. We also test our methods on synthetic and benchmark graph datasets, and compare the results with previous vector representations of $1$-parameter and $2$-parameter persistence modules.

Humans are still the best lossy image compressors

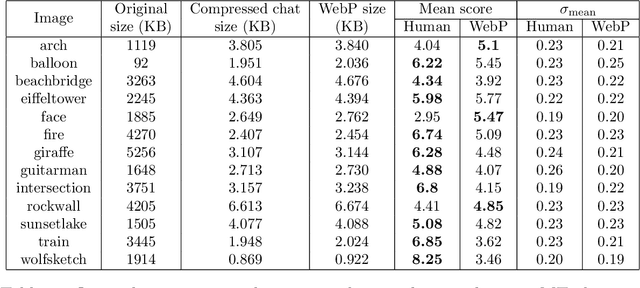
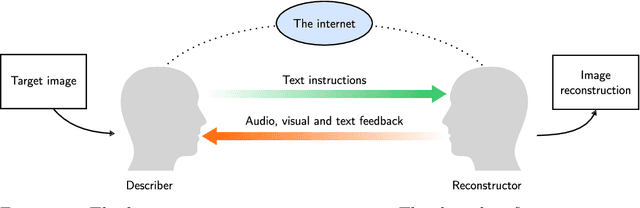
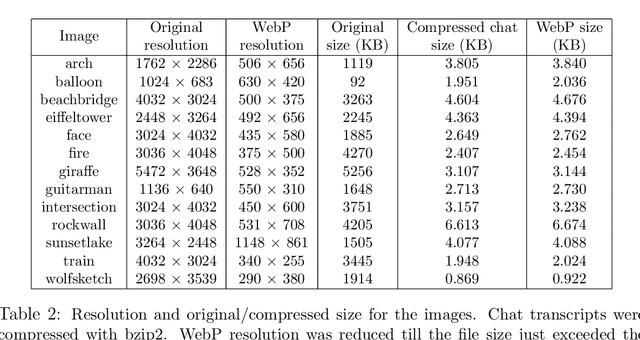
Lossy image compression has been studied extensively in the context of typical loss functions such as RMSE, MS-SSIM, etc. However, it is not well understood what loss function might be most appropriate for human perception. Furthermore, the availability of massive public image datasets appears to have hardly been exploited in image compression. In this work, we perform compression experiments in which one human describes images to another, using publicly available images and text instructions. These image reconstructions are rated by human scorers on the Amazon Mechanical Turk platform and compared to reconstructions obtained by existing image compressors. In our experiments, the humans outperform the state of the art compressor WebP in the MTurk survey on most images, which shows that there is significant room for improvement in image compression for human perception. The images, results and additional data is available at https://compression.stanford.edu/human-compression.