Humans are still the best lossy image compressors

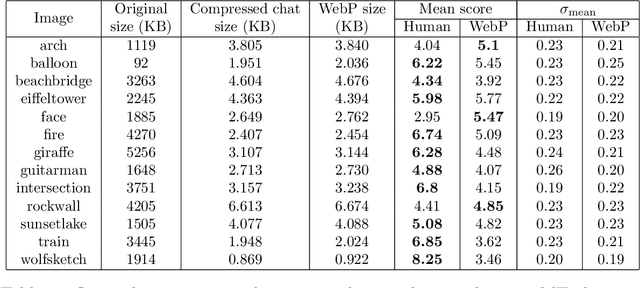
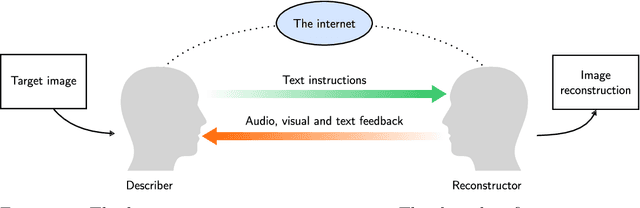
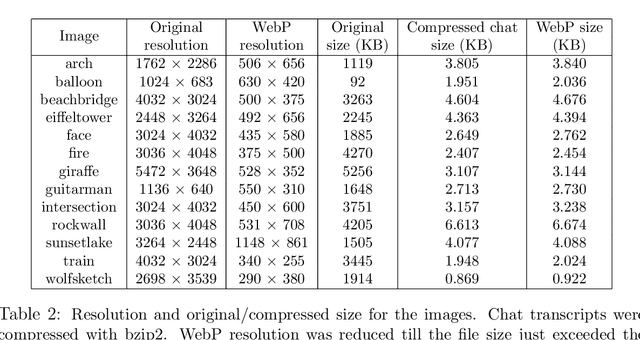
Lossy image compression has been studied extensively in the context of typical loss functions such as RMSE, MS-SSIM, etc. However, it is not well understood what loss function might be most appropriate for human perception. Furthermore, the availability of massive public image datasets appears to have hardly been exploited in image compression. In this work, we perform compression experiments in which one human describes images to another, using publicly available images and text instructions. These image reconstructions are rated by human scorers on the Amazon Mechanical Turk platform and compared to reconstructions obtained by existing image compressors. In our experiments, the humans outperform the state of the art compressor WebP in the MTurk survey on most images, which shows that there is significant room for improvement in image compression for human perception. The images, results and additional data is available at https://compression.stanford.edu/human-compression.

Estimating the Fundamental Limits is Easier than Achieving the Fundamental Limits

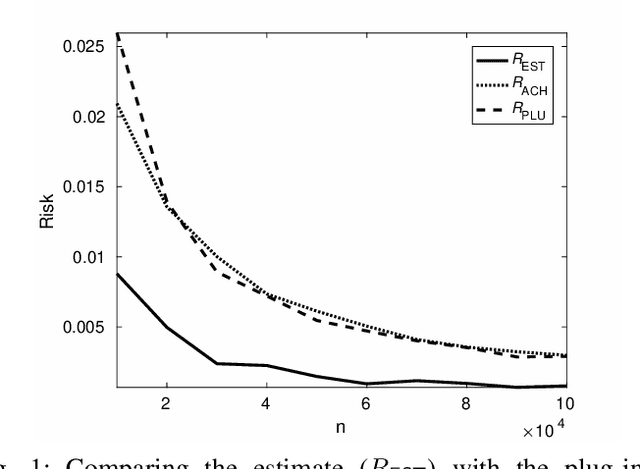
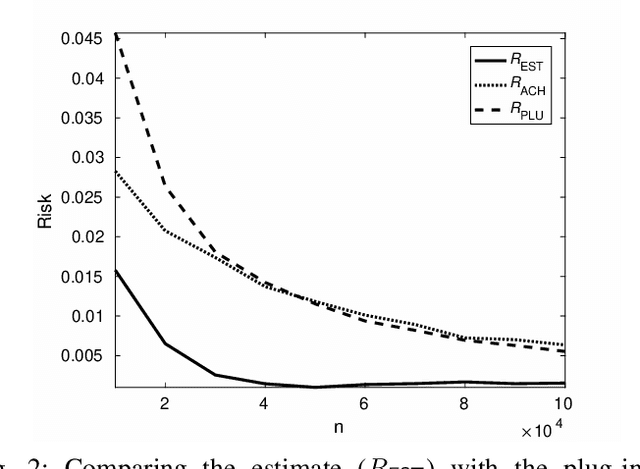
We show through case studies that it is easier to estimate the fundamental limits of data processing than to construct explicit algorithms to achieve those limits. Focusing on binary classification, data compression, and prediction under logarithmic loss, we show that in the finite space setting, when it is possible to construct an estimator of the limits with vanishing error with $n$ samples, it may require at least $n\ln n$ samples to construct an explicit algorithm to achieve the limits.