D-GRIL: End-to-End Topological Learning with 2-parameter Persistence

End-to-end topological learning using 1-parameter persistence is well-known. We show that the framework can be enhanced using 2-parameter persistence by adopting a recently introduced 2-parameter persistence based vectorization technique called GRIL. We establish a theoretical foundation of differentiating GRIL producing D-GRIL. We show that D-GRIL can be used to learn a bifiltration function on standard benchmark graph datasets. Further, we exhibit that this framework can be applied in the context of bio-activity prediction in drug discovery.

GEFL: Extended Filtration Learning for Graph Classification

Extended persistence is a technique from topological data analysis to obtain global multiscale topological information from a graph. This includes information about connected components and cycles that are captured by the so-called persistence barcodes. We introduce extended persistence into a supervised learning framework for graph classification. Global topological information, in the form of a barcode with four different types of bars and their explicit cycle representatives, is combined into the model by the readout function which is computed by extended persistence. The entire model is end-to-end differentiable. We use a link-cut tree data structure and parallelism to lower the complexity of computing extended persistence, obtaining a speedup of more than 60x over the state-of-the-art for extended persistence computation. This makes extended persistence feasible for machine learning. We show that, under certain conditions, extended persistence surpasses both the WL[1] graph isomorphism test and 0-dimensional barcodes in terms of expressivity because it adds more global (topological) information. In particular, arbitrarily long cycles can be represented, which is difficult for finite receptive field message passing graph neural networks. Furthermore, we show the effectiveness of our method on real world datasets compared to many existing recent graph representation learning methods.

Expressive Higher-Order Link Prediction through Hypergraph Symmetry Breaking

A hypergraph consists of a set of nodes along with a collection of subsets of the nodes called hyperedges. Higher-order link prediction is the task of predicting the existence of a missing hyperedge in a hypergraph. A hyperedge representation learned for higher order link prediction is fully expressive when it does not lose distinguishing power up to an isomorphism. Many existing hypergraph representation learners, are bounded in expressive power by the Generalized Weisfeiler Lehman-1 (GWL-1) algorithm, a generalization of the Weisfeiler Lehman-1 algorithm. However, GWL-1 has limited expressive power. In fact, induced subhypergraphs with identical GWL-1 valued nodes are indistinguishable. Furthermore, message passing on hypergraphs can already be computationally expensive, especially on GPU memory. To address these limitations, we devise a preprocessing algorithm that can identify certain regular subhypergraphs exhibiting symmetry. Our preprocessing algorithm runs once with complexity the size of the input hypergraph. During training, we randomly replace subhypergraphs identified by the algorithm with covering hyperedges to break symmetry. We show that our method improves the expressivity of GWL-1. Our extensive experiments also demonstrate the effectiveness of our approach for higher-order link prediction on both graph and hypergraph datasets with negligible change in computation.

GRIL: A $2$-parameter Persistence Based Vectorization for Machine Learning

$1$-parameter persistent homology, a cornerstone in Topological Data Analysis (TDA), studies the evolution of topological features such as connected components and cycles hidden in data. It has been applied to enhance the representation power of deep learning models, such as Graph Neural Networks (GNNs). To enrich the representations of topological features, here we propose to study $2$-parameter persistence modules induced by bi-filtration functions. In order to incorporate these representations into machine learning models, we introduce a novel vector representation called Generalized Rank Invariant Landscape \textsc{Gril} for $2$-parameter persistence modules. We show that this vector representation is $1$-Lipschitz stable and differentiable with respect to underlying filtration functions and can be easily integrated into machine learning models to augment encoding topological features. We present an algorithm to compute the vector representation efficiently. We also test our methods on synthetic and benchmark graph datasets, and compare the results with previous vector representations of $1$-parameter and $2$-parameter persistence modules.

Topological structure of complex predictions

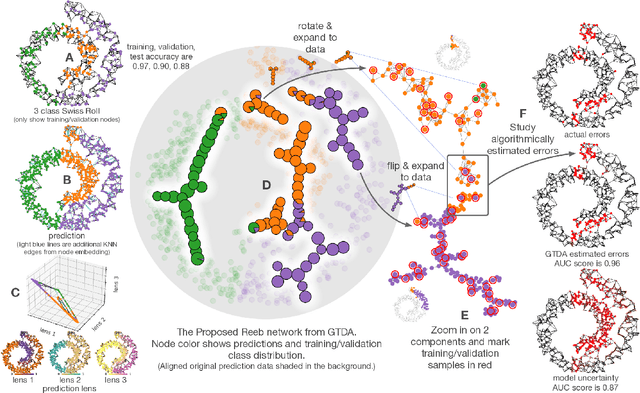
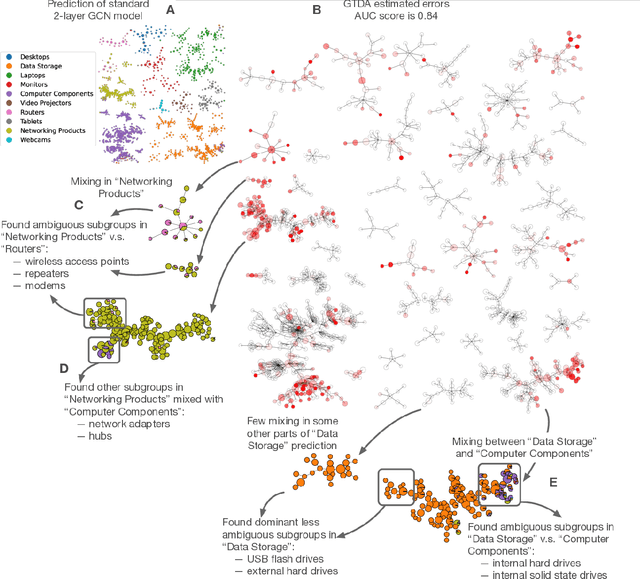
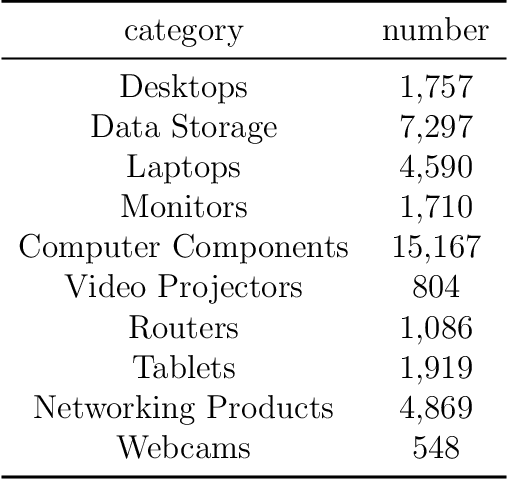
Complex prediction models such as deep learning are the output from fitting machine learning, neural networks, or AI models to a set of training data. These are now standard tools in science. A key challenge with the current generation of models is that they are highly parameterized, which makes describing and interpreting the prediction strategies difficult. We use topological data analysis to transform these complex prediction models into pictures representing a topological view. The result is a map of the predictions that enables inspection. The methods scale up to large datasets across different domains and enable us to detect labeling errors in training data, understand generalization in image classification, and inspect predictions of likely pathogenic mutations in the BRCA1 gene.

Road Network Reconstruction from Satellite Images with Machine Learning Supported by Topological Methods

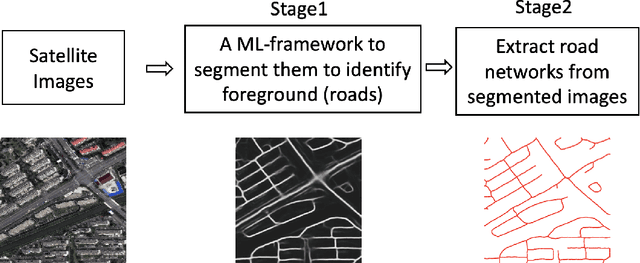
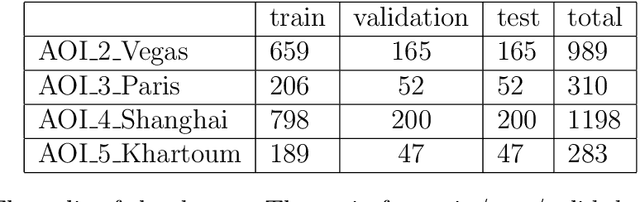
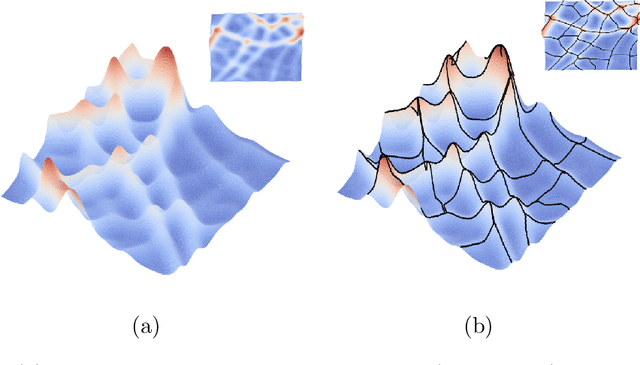
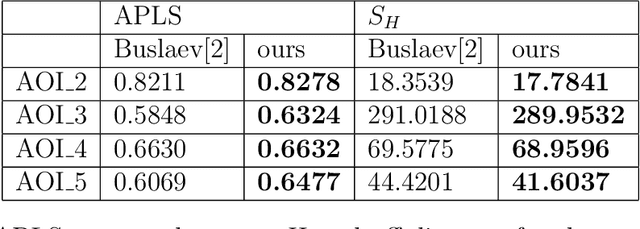
Automatic Extraction of road network from satellite images is a goal that can benefit and even enable new technologies. Methods that combine machine learning (ML) and computer vision have been proposed in recent years which make the task semi-automatic by requiring the user to provide curated training samples. The process can be fully automatized if training samples can be produced algorithmically. Of course, this requires a robust algorithm that can reconstruct the road networks from satellite images reliably so that the output can be fed as training samples. In this work, we develop such a technique by infusing a persistence-guided discrete Morse based graph reconstruction algorithm into ML framework. We elucidate our contributions in two phases. First, in a semi-automatic framework, we combine a discrete-Morse based graph reconstruction algorithm with an existing CNN framework to segment input satellite images. We show that this leads to reconstructions with better connectivity and less noise. Next, in a fully automatic framework, we leverage the power of the discrete-Morse based graph reconstruction algorithm to train a CNN from a collection of images without labelled data and use the same algorithm to produce the final output from the segmented images created by the trained CNN. We apply the discrete-Morse based graph reconstruction algorithm iteratively to improve the accuracy of the CNN. We show promising experimental results of this new framework on datasets from SpaceNet Challenge.