Time to Embed: Unlocking Foundation Models for Time Series with Channel Descriptions

Traditional time series models are task-specific and often depend on dataset-specific training and extensive feature engineering. While Transformer-based architectures have improved scalability, foundation models, commonplace in text, vision, and audio, remain under-explored for time series and are largely restricted to forecasting. We introduce $\textbf{CHARM}$, a foundation embedding model for multivariate time series that learns shared, transferable, and domain-aware representations. To address the unique difficulties of time series foundation learning, $\textbf{CHARM}$ incorporates architectural innovations that integrate channel-level textual descriptions while remaining invariant to channel order. The model is trained using a Joint Embedding Predictive Architecture (JEPA), with novel augmentation schemes and a loss function designed to improve interpretability and training stability. Our $7$M-parameter model achieves state-of-the-art performance across diverse downstream tasks, setting a new benchmark for time series representation learning.

A Scalable and Distributed Solution to the Inertial Motion Capture Problem

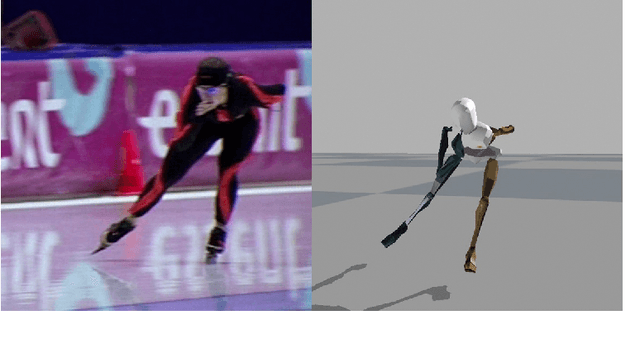
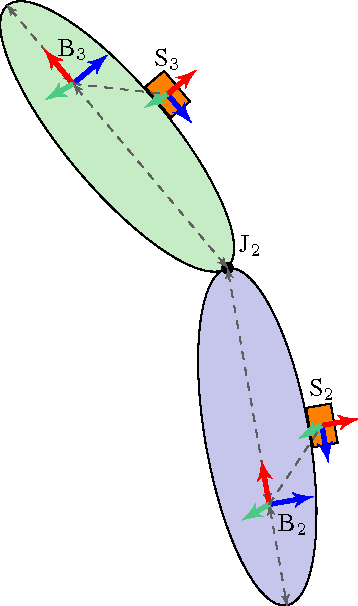
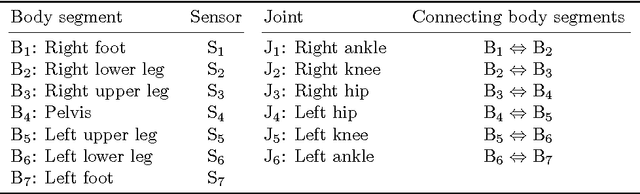
In inertial motion capture, a multitude of body segments are equipped with inertial sensors, consisting of 3D accelerometers and 3D gyroscopes. Using an optimization-based approach to solve the motion capture problem allows for natural inclusion of biomechanical constraints and for modeling the connection of the body segments at the joint locations. The computational complexity of solving this problem grows both with the length of the data set and with the number of sensors and body segments considered. In this work, we present a scalable and distributed solution to this problem using tailored message passing, capable of exploiting the structure that is inherent in the problem. As a proof-of-concept we apply our algorithm to data from a lower body configuration.

Scalable Anomaly Detection in Large Homogenous Populations

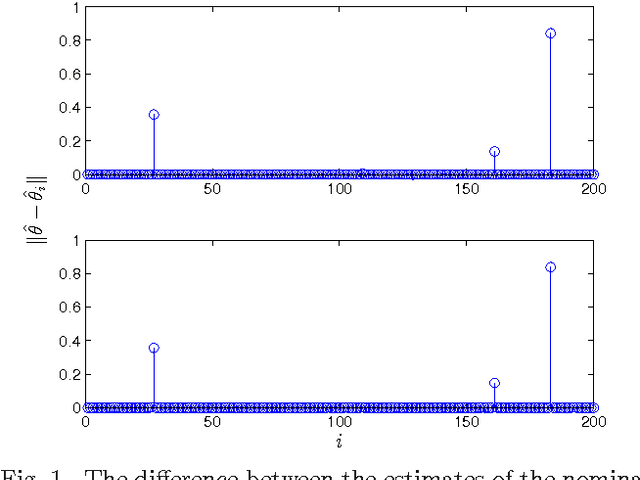
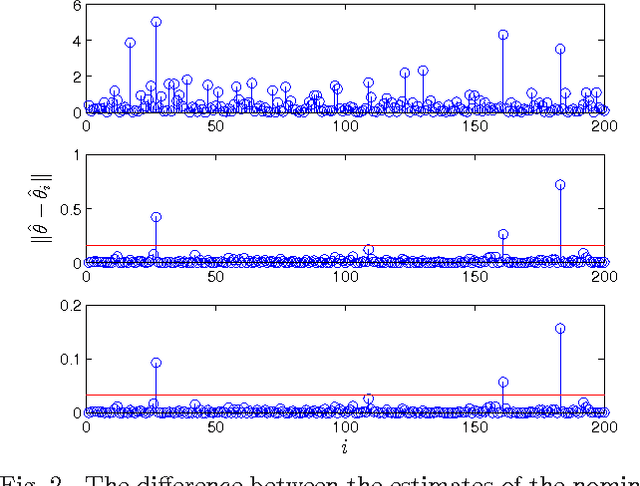
Anomaly detection in large populations is a challenging but highly relevant problem. The problem is essentially a multi-hypothesis problem, with a hypothesis for every division of the systems into normal and anomal systems. The number of hypothesis grows rapidly with the number of systems and approximate solutions become a necessity for any problems of practical interests. In the current paper we take an optimization approach to this multi-hypothesis problem. We first observe that the problem is equivalent to a non-convex combinatorial optimization problem. We then relax the problem to a convex problem that can be solved distributively on the systems and that stays computationally tractable as the number of systems increase. An interesting property of the proposed method is that it can under certain conditions be shown to give exactly the same result as the combinatorial multi-hypothesis problem and the relaxation is hence tight.