Invariant filtering for wheeled vehicle localization with unknown wheel radius and unknown GNSS lever arm

We consider the problem of observer design for a nonholonomic car (more generally a wheeled robot) equipped with wheel speeds with unknown wheel radius, and whose position is measured via a GNSS antenna placed at an unknown position in the car. In a tutorial and unified exposition, we recall the recent theory of two-frame systems within the field of invariant Kalman filtering. We then show how to adapt it geometrically to address the considered problem, although it seems at first sight out of its scope. This yields an invariant extended Kalman filter having autonomous error equations, and state-independent Jacobians, which is shown to work remarkably well in simulations. The proposed novel construction thus extends the application scope of invariant filtering.

Backpropagation-Based Analytical Derivatives of EKF Covariance for Active Sensing

To enhance accuracy of robot state estimation, active sensing (or perception-aware) methods seek trajectories that maximize the information gathered by the sensors. To this aim, one possibility is to seek trajectories that minimize the (estimation error) covariance matrix output by an extended Kalman filter (EKF), w.r.t. its control inputs over a given horizon. However, this is computationally demanding. In this article, we derive novel backpropagation analytical formulas for the derivatives of the covariance matrices of an EKF w.r.t. all its inputs. We then leverage the obtained analytical gradients as an enabling technology to derive perception-aware optimal motion plans. Simulations validate the approach, showcasing improvements in execution time, notably over PyTorch's automatic differentiation. Experimental results on a real vehicle also support the method.

Variational Gaussian approximation of the Kushner optimal filter

In estimation theory, the Kushner equation provides the evolution of the probability density of the state of a dynamical system given continuous-time observations. Building upon our recent work, we propose a new way to approximate the solution of the Kushner equation through tractable variational Gaussian approximations of two proximal losses associated with the propagation and Bayesian update of the probability density. The first is a proximal loss based on the Wasserstein metric and the second is a proximal loss based on the Fisher metric. The solution to this last proximal loss is given by implicit updates on the mean and covariance that we proposed earlier. These two variational updates can be fused and shown to satisfy a set of stochastic differential equations on the Gaussian's mean and covariance matrix. This Gaussian flow is consistent with the Kalman-Bucy and Riccati flows in the linear case and generalize them in the nonlinear one.

Invariant Smoothing for Localization: Including the IMU Biases

In this article we investigate smoothing (i.e., optimisation-based) estimation techniques for robot localization using an IMU aided by other localization sensors. We more particularly focus on Invariant Smoothing (IS), a variant based on the use of nontrivial Lie groups from robotics. We study the recently introduced Two Frames Group (TFG), and prove it can fit into the framework of Invariant Smoothing in order to better take into account the IMU biases, as compared to the state-of-the-art in robotics. Experiments based on the KITTI dataset show the proposed framework compares favorably to the state-of-the-art smoothing methods in terms of robustness in some challenging situations.

Variational inference via Wasserstein gradient flows

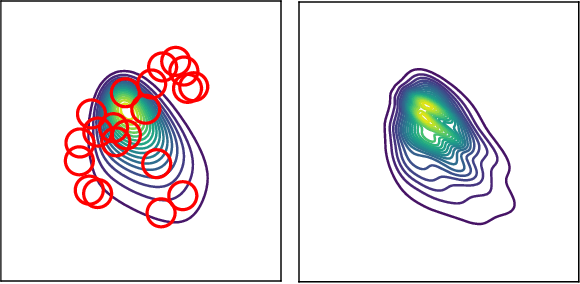
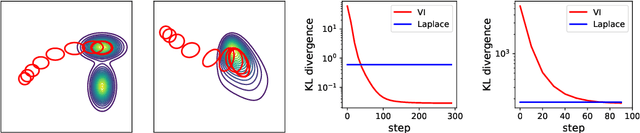
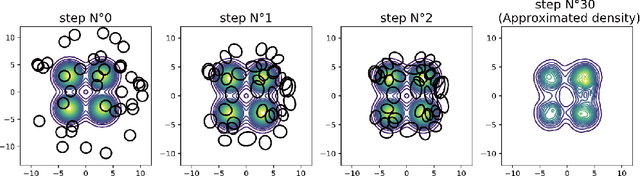
Along with Markov chain Monte Carlo (MCMC) methods, variational inference (VI) has emerged as a central computational approach to large-scale Bayesian inference. Rather than sampling from the true posterior $\pi$, VI aims at producing a simple but effective approximation $\hat \pi$ to $\pi$ for which summary statistics are easy to compute. However, unlike the well-studied MCMC methodology, VI is still poorly understood and dominated by heuristics. In this work, we propose principled methods for VI, in which $\hat \pi$ is taken to be a Gaussian or a mixture of Gaussians, which rest upon the theory of gradient flows on the Bures-Wasserstein space of Gaussian measures. Akin to MCMC, it comes with strong theoretical guarantees when $\pi$ is log-concave.

Factor Graph-Based Smoothing Without Matrix Inversion for Highly Precise Localization

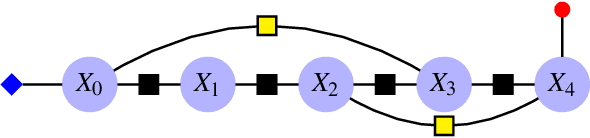
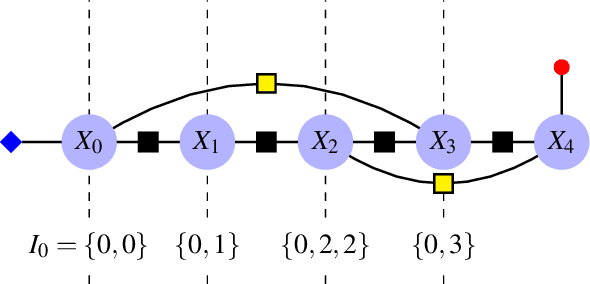
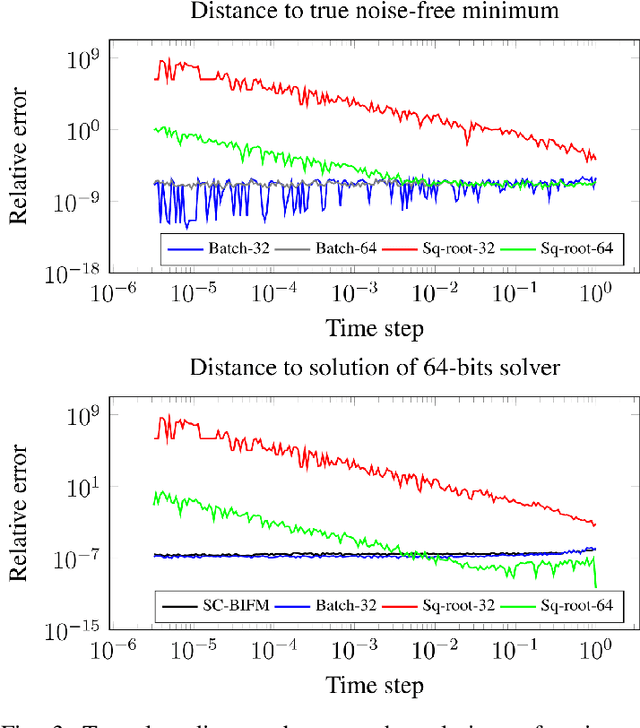
We consider the problem of localizing a manned, semi-autonomous, or autonomous vehicle in the environment using information coming from the vehicle's sensors, a problem known as navigation or simultaneous localization and mapping (SLAM) depending on the context. To infer knowledge from sensors' measurements, while drawing on a priori knowledge about the vehicle's dynamics, modern approaches solve an optimization problem to compute the most likely trajectory given all past observations, an approach known as smoothing. Improving smoothing solvers is an active field of research in the SLAM community. Most work is focused on reducing computation load by inverting the involved linear system while preserving its sparsity. The present paper raises an issue which, to the knowledge of the authors, has not been addressed yet: standard smoothing solvers require explicitly using the inverse of sensor noise covariance matrices. This means the parameters that reflect the noise magnitude must be sufficiently large for the smoother to properly function. When matrices are close to singular, which is the case when using high precision modern inertial measurement units (IMU), numerical issues necessarily arise, especially with 32-bits implementation demanded by most industrial aerospace applications. We discuss these issues and propose a solution that builds upon the Kalman filter to improve smoothing algorithms. We then leverage the results to devise a localization algorithm based on fusion of IMU and vision sensors. Successful real experiments using an actual car equipped with a tactical grade high performance IMU and a LiDAR illustrate the relevance of the approach to the field of autonomous vehicles.

Associating Uncertainty to Extended Poses for on Lie Group IMU Preintegration with Rotating Earth

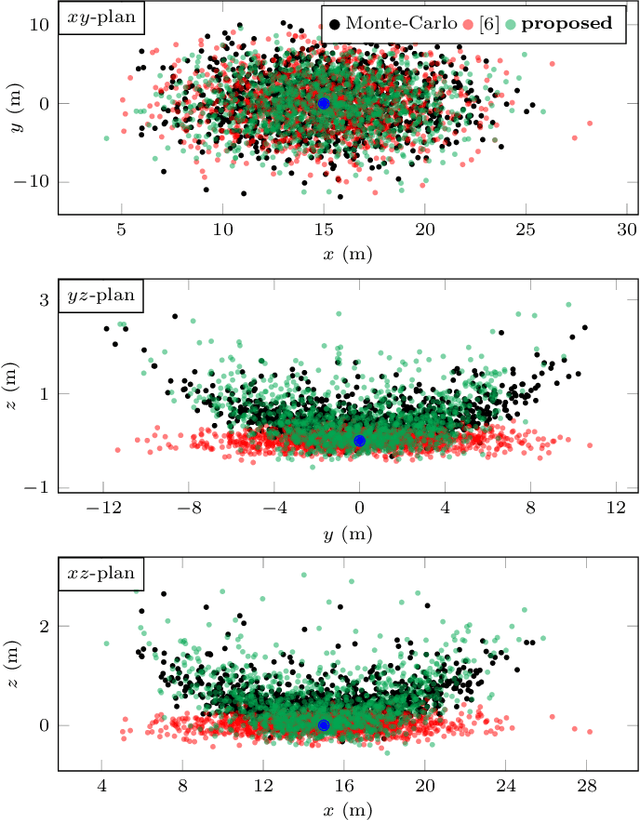
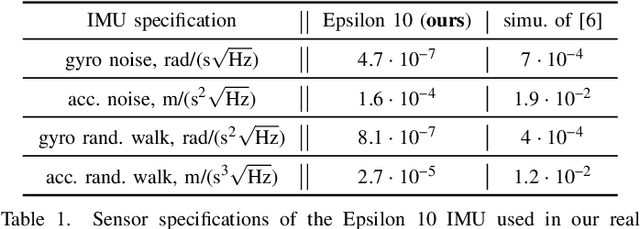
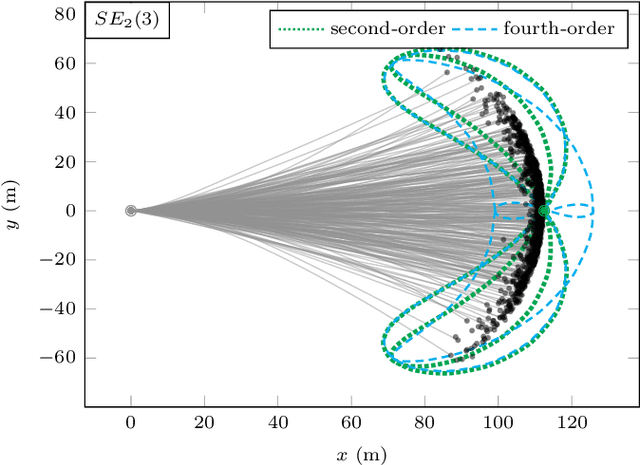
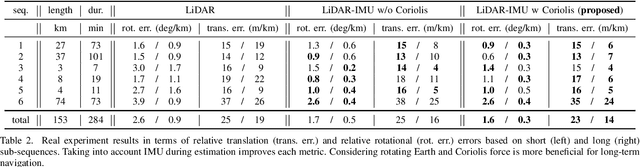
The recently introduced matrix group SE2(3) provides a 5x5 matrix representation for the orientation, velocity and position of an object in the 3-D space, a triplet we call ''extended pose''. In this paper we build on this group to develop a theory to associate uncertainty with extended poses represented by 5x5 matrices. Our approach is particularly suited to describe how uncertainty propagates when the extended pose represents the state of an Inertial Measurement Unit (IMU). In particular it allows revisiting the theory of IMU preintegration on manifold and reaching a further theoretic level in this field. Exact preintegration formulas that account for rotating Earth, that is, centrifugal force and Coriolis force, are derived as a byproduct, and the factors are shown to be more accurate. The approach is validated through extensive simulations and applied to sensor-fusion where a loosely-coupled fixed-lag smoother fuses IMU and LiDAR on one hour long experiments using our experimental car. It shows how handling rotating Earth may be beneficial for long-term navigation within incremental smoothing algorithms.

A New Approach to 3D ICP Covariance Estimation for Mobile Robotics

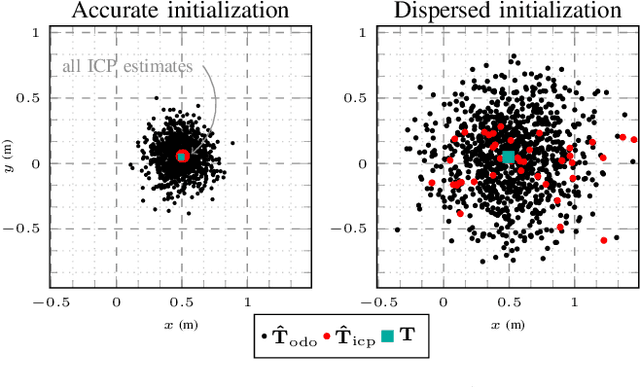
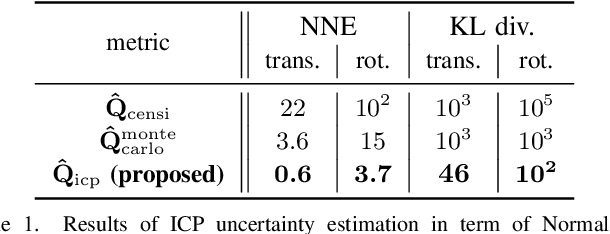
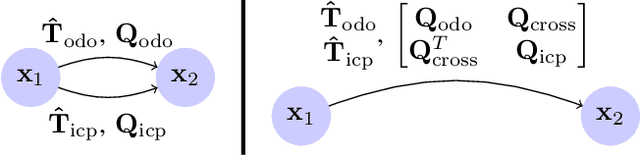
In mobile robotics, scan matching of point clouds using Iterative Closest Point (ICP) allows estimating sensor displacements. It may prove important to assess the associated uncertainty about the obtained rigid transformation, especially for sensor fusion purposes. In this paper we propose a novel approach to 3D ICP covariance computation that accounts for all the sources of errors as listed in Censi's pioneering work, namely wrong convergence, underconstrained situations, and sensor noise. Our approach builds on two facts. First, ICP is not a standard sensor: owing to wrong convergence the concept of ICP covariance per se is actually meaningless, as the dispersion in the ICP outputs may largely depend on the accuracy of the initialization, and is thus inherently related to the prior uncertainty on the displacement. We capture this using the unscented transform, which also reflects correlations between initial and final uncertainties. Then, assuming white sensor noise leads to overoptimism: ICP is biased, owing to e.g. calibration biases, which we account for. Our solution is tested on publicly available real data ranging from structured to unstructured environments, where our algorithm predicts consistent results with actual uncertainty, and compares very favorably to previous methods. We finally demonstrate the benefits of our method for pose-graph localization, where our approach improves accuracy and robustness of the estimates.

AI-IMU Dead-Reckoning

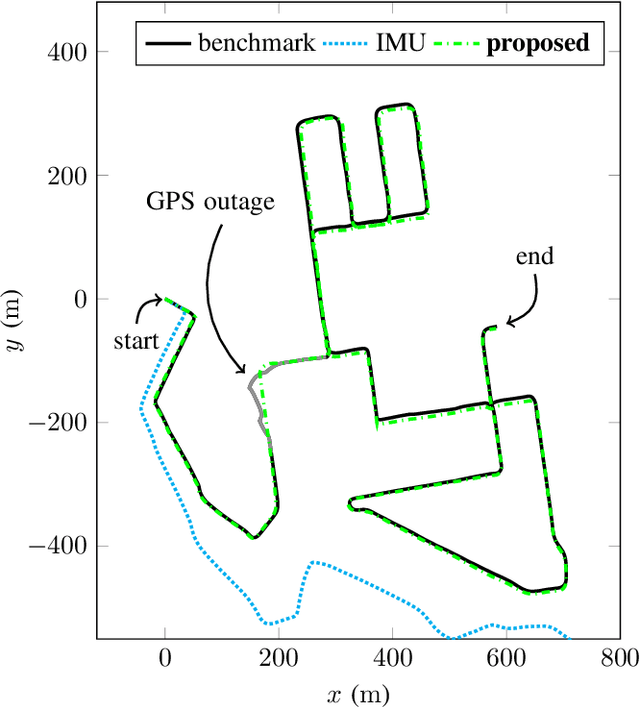
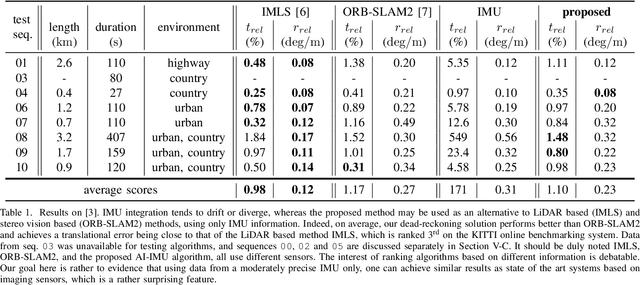
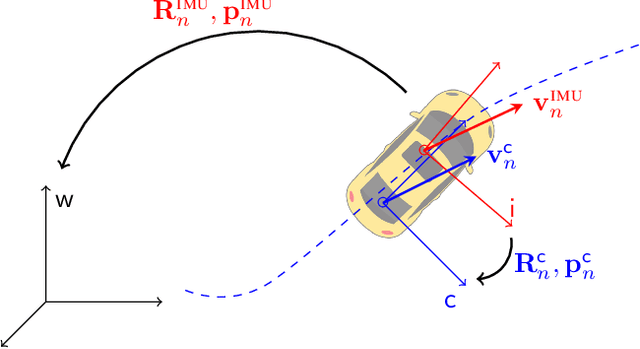
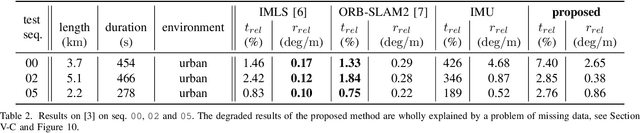
In this paper we propose a novel accurate method for dead-reckoning of wheeled vehicles based only on an Inertial Measurement Unit (IMU). In the context of intelligent vehicles, robust and accurate dead-reckoning based on the IMU may prove useful to correlate feeds from imaging sensors, to safely navigate through obstructions, or for safe emergency stops in the extreme case of exteroceptive sensors failure. The key components of the method are the Kalman filter and the use of deep neural networks to dynamically adapt the noise parameters of the filter. The method is tested on the KITTI odometry dataset, and our dead-reckoning inertial method based only on the IMU accurately estimates 3D position, velocity, orientation of the vehicle and self-calibrates the IMU biases. We achieve on average a 1.10% translational error and the algorithm competes with top-ranked methods which, by contrast, use LiDAR or stereo vision. We make our implementation open-source at: https://github.com/mbrossar/ai-imu-dr

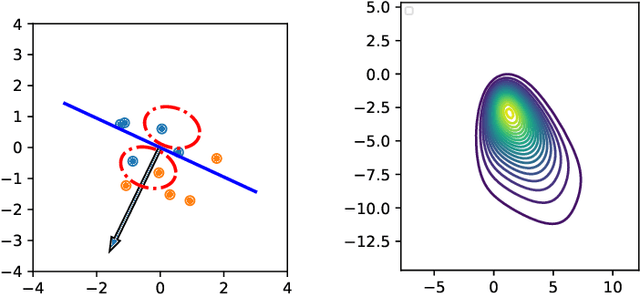
Exploiting Symmetries to Design EKFs with Consistency Properties for Navigation and SLAM

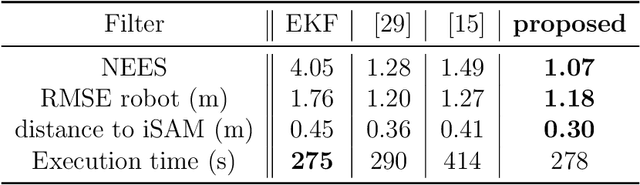
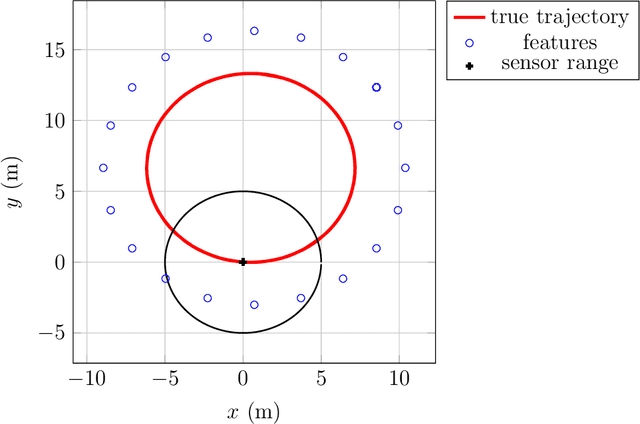
The Extended Kalman Filter (EKF) is both the historical algorithm for multi-sensor fusion and still state of the art in numerous industrial applications. However, it may prove inconsistent in the presence of unobservability under a group of transformations. In this paper we first build an alternative EKF based on an alternative nonlinear state error. This EKF is intimately related to the theory of the Invariant EKF (IEKF). Then, under a simple compatibility assumption between the error and the transformation group, we prove the linearized model of the alternative EKF automatically captures the unobservable directions, and many desirable properties of the linear case then directly follow. This provides a novel fundamental result in filtering theory. We apply the theory to multi-sensor fusion for navigation, when all the sensors are attached to the vehicle and do not have access to absolute information, as typically occurs in GPS-denied environments. In the context of Simultaneous Localization And Mapping (SLAM), Monte-Carlo runs and comparisons to OC-EKF, robocentric EKF, and optimization-based smoothing algorithms (iSAM) illustrate the results. The proposed EKF is also proved to outperform standard EKF and to achieve comparable performance to iSAM on a publicly available real dataset for multi-robot SLAM.