Invariant filtering for wheeled vehicle localization with unknown wheel radius and unknown GNSS lever arm

We consider the problem of observer design for a nonholonomic car (more generally a wheeled robot) equipped with wheel speeds with unknown wheel radius, and whose position is measured via a GNSS antenna placed at an unknown position in the car. In a tutorial and unified exposition, we recall the recent theory of two-frame systems within the field of invariant Kalman filtering. We then show how to adapt it geometrically to address the considered problem, although it seems at first sight out of its scope. This yields an invariant extended Kalman filter having autonomous error equations, and state-independent Jacobians, which is shown to work remarkably well in simulations. The proposed novel construction thus extends the application scope of invariant filtering.

Invariant Smoothing for Localization: Including the IMU Biases

In this article we investigate smoothing (i.e., optimisation-based) estimation techniques for robot localization using an IMU aided by other localization sensors. We more particularly focus on Invariant Smoothing (IS), a variant based on the use of nontrivial Lie groups from robotics. We study the recently introduced Two Frames Group (TFG), and prove it can fit into the framework of Invariant Smoothing in order to better take into account the IMU biases, as compared to the state-of-the-art in robotics. Experiments based on the KITTI dataset show the proposed framework compares favorably to the state-of-the-art smoothing methods in terms of robustness in some challenging situations.

Invariant Smoothing with low process noise

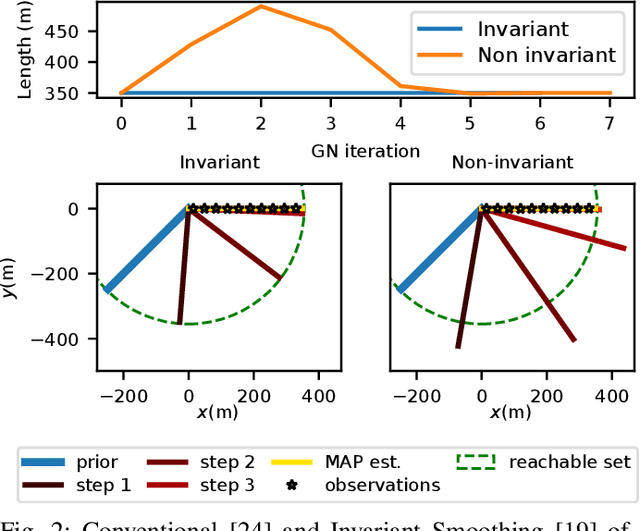
In this paper we address smoothing-that is, optimisation-based-estimation techniques for localisation problems in the case where motion sensors are very accurate. Our mathematical analysis focuses on the difficult limit case where motion sensors are infinitely precise, resulting in the absence of process noise. Then the formulation degenerates, as the dynamical model that serves as a soft constraint becomes an equality constraint, and conventional smoothing methods are not able to fully respect it. By contrast, once an appropriate Lie group embedding has been found, we prove theoretically that invariant smoothing gracefully accommodates this limit case in that the estimates tend to be consistent with the induced constraints when the noise tends to zero. Simulations on the important problem of initial alignement in inertial navigation show that, in a low noise setting, invariant smoothing may favorably compare to state-of-the-art smoothers when using precise inertial measurements units (IMU).

Factor Graph-Based Smoothing Without Matrix Inversion for Highly Precise Localization

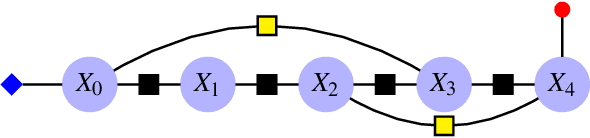
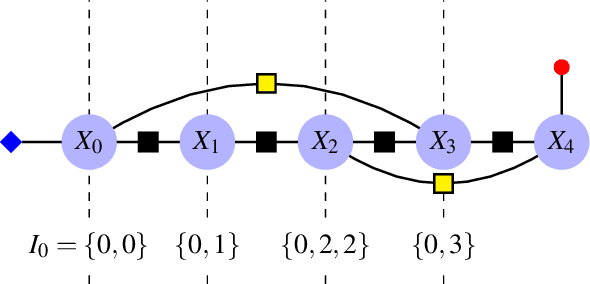
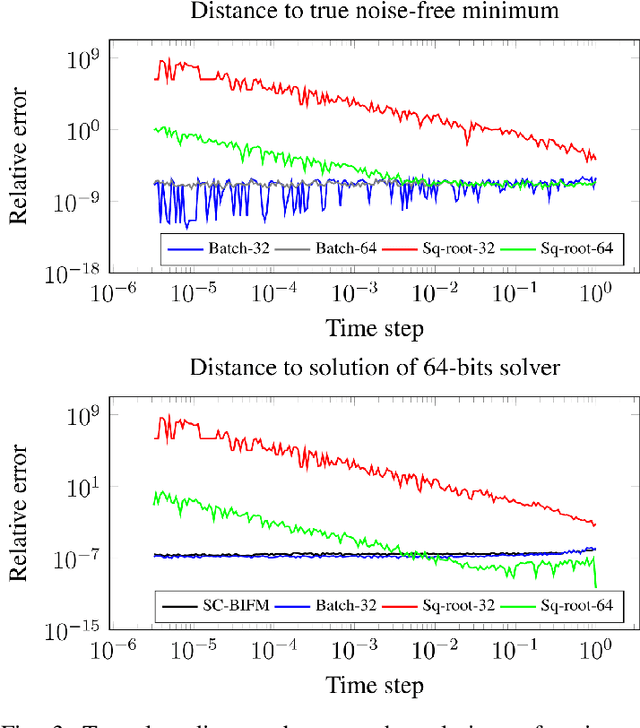
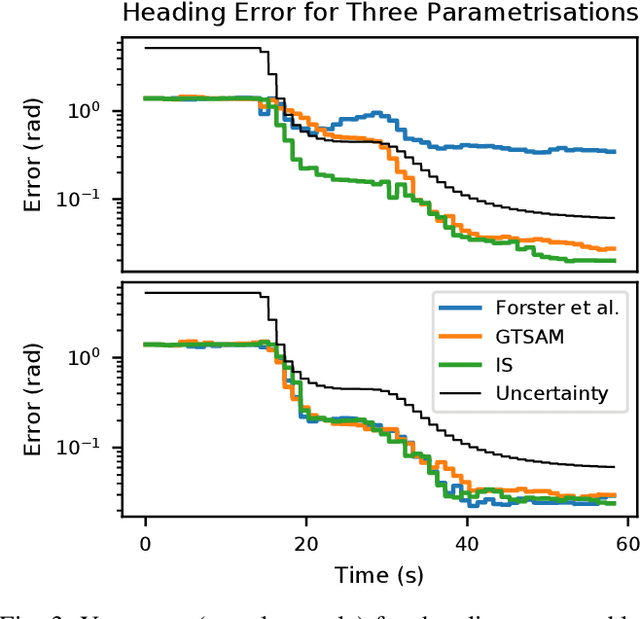
We consider the problem of localizing a manned, semi-autonomous, or autonomous vehicle in the environment using information coming from the vehicle's sensors, a problem known as navigation or simultaneous localization and mapping (SLAM) depending on the context. To infer knowledge from sensors' measurements, while drawing on a priori knowledge about the vehicle's dynamics, modern approaches solve an optimization problem to compute the most likely trajectory given all past observations, an approach known as smoothing. Improving smoothing solvers is an active field of research in the SLAM community. Most work is focused on reducing computation load by inverting the involved linear system while preserving its sparsity. The present paper raises an issue which, to the knowledge of the authors, has not been addressed yet: standard smoothing solvers require explicitly using the inverse of sensor noise covariance matrices. This means the parameters that reflect the noise magnitude must be sufficiently large for the smoother to properly function. When matrices are close to singular, which is the case when using high precision modern inertial measurement units (IMU), numerical issues necessarily arise, especially with 32-bits implementation demanded by most industrial aerospace applications. We discuss these issues and propose a solution that builds upon the Kalman filter to improve smoothing algorithms. We then leverage the results to devise a localization algorithm based on fusion of IMU and vision sensors. Successful real experiments using an actual car equipped with a tactical grade high performance IMU and a LiDAR illustrate the relevance of the approach to the field of autonomous vehicles.

Associating Uncertainty to Extended Poses for on Lie Group IMU Preintegration with Rotating Earth

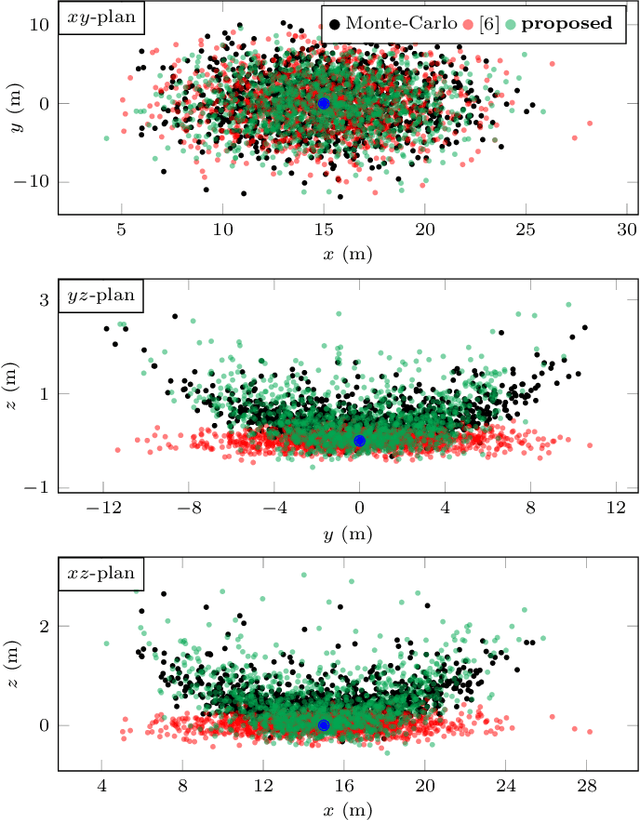
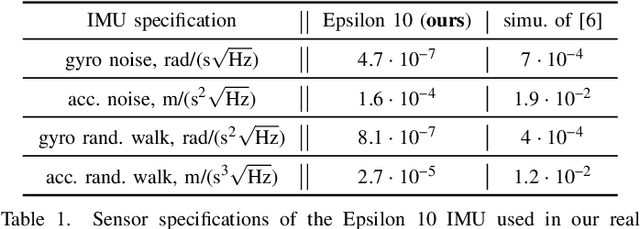
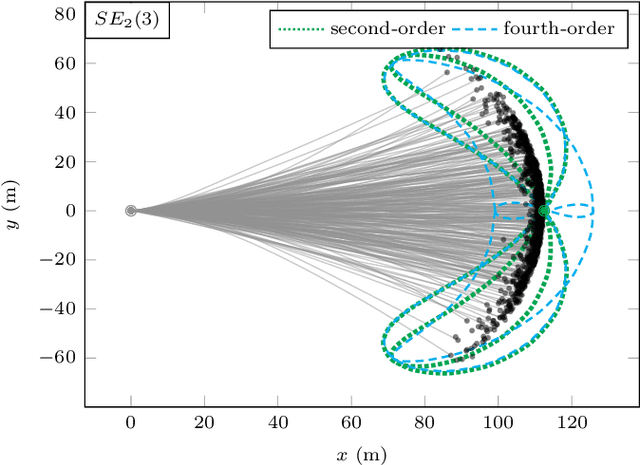
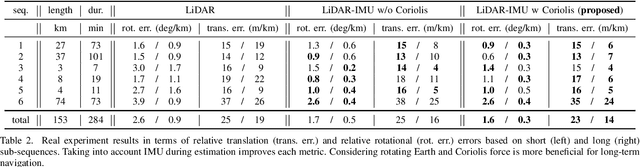
The recently introduced matrix group SE2(3) provides a 5x5 matrix representation for the orientation, velocity and position of an object in the 3-D space, a triplet we call ''extended pose''. In this paper we build on this group to develop a theory to associate uncertainty with extended poses represented by 5x5 matrices. Our approach is particularly suited to describe how uncertainty propagates when the extended pose represents the state of an Inertial Measurement Unit (IMU). In particular it allows revisiting the theory of IMU preintegration on manifold and reaching a further theoretic level in this field. Exact preintegration formulas that account for rotating Earth, that is, centrifugal force and Coriolis force, are derived as a byproduct, and the factors are shown to be more accurate. The approach is validated through extensive simulations and applied to sensor-fusion where a loosely-coupled fixed-lag smoother fuses IMU and LiDAR on one hour long experiments using our experimental car. It shows how handling rotating Earth may be beneficial for long-term navigation within incremental smoothing algorithms.

Geomstats: A Python Package for Riemannian Geometry in Machine Learning

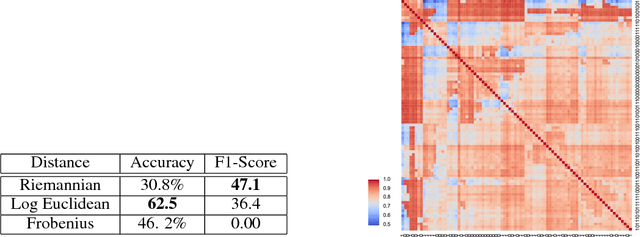
We introduce Geomstats, an open-source Python toolbox for computations and statistics on nonlinear manifolds, such as hyperbolic spaces, spaces of symmetric positive definite matrices, Lie groups of transformations, and many more. We provide object-oriented and extensively unit-tested implementations. Among others, manifolds come equipped with families of Riemannian metrics, with associated exponential and logarithmic maps, geodesics and parallel transport. Statistics and learning algorithms provide methods for estimation, clustering and dimension reduction on manifolds. All associated operations are vectorized for batch computation and provide support for different execution backends, namely NumPy, PyTorch and TensorFlow, enabling GPU acceleration. This paper presents the package, compares it with related libraries and provides relevant code examples. We show that Geomstats provides reliable building blocks to foster research in differential geometry and statistics, and to democratize the use of Riemannian geometry in machine learning applications. The source code is freely available under the MIT license at \url{geomstats.ai}.

Invariant Smoothing on Lie Groups

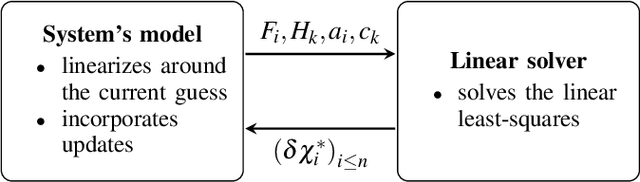
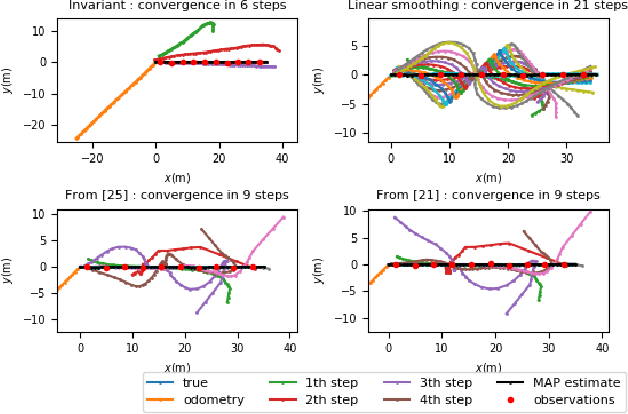
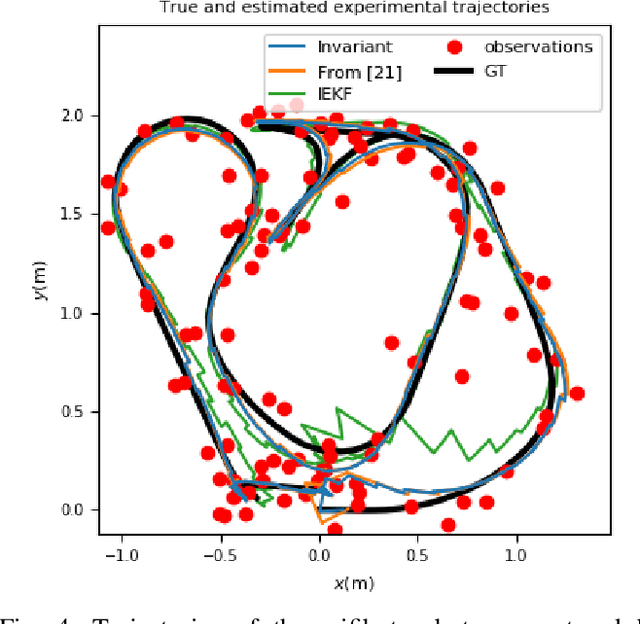
In this paper we propose a (non-linear) smoothing algorithm for group-affine observation systems, a recently introduced class of estimation problems on Lie groups that bear a particular structure. As most non-linear smoothing methods, the proposed algorithm is based on a maximum a posteriori estimator, determined by optimization. But owing to the specific properties of the considered class of problems, the involved linearizations are proved to have a form of independence with respect to the current estimates, leveraged to avoid (partially or sometimes totally) the need to relinearize. The method is validated on a robot localization example, both in simulations and on real experimental data.