Variational Inference with Mixtures of Isotropic Gaussians

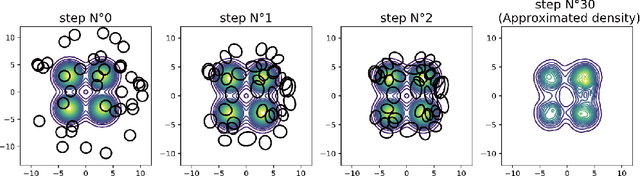
Variational inference (VI) is a popular approach in Bayesian inference, that looks for the best approximation of the posterior distribution within a parametric family, minimizing a loss that is typically the (reverse) Kullback-Leibler (KL) divergence. In this paper, we focus on the following parametric family: mixtures of isotropic Gaussians (i.e., with diagonal covariance matrices proportional to the identity) and uniform weights. We develop a variational framework and provide efficient algorithms suited for this family. In contrast with mixtures of Gaussian with generic covariance matrices, this choice presents a balance between accurate approximations of multimodal Bayesian posteriors, while being memory and computationally efficient. Our algorithms implement gradient descent on the location of the mixture components (the modes of the Gaussians), and either (an entropic) Mirror or Bures descent on their variance parameters. We illustrate the performance of our algorithms on numerical experiments.

Variational Gaussian approximation of the Kushner optimal filter

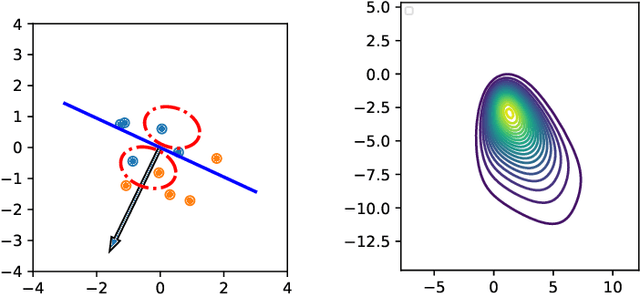
In estimation theory, the Kushner equation provides the evolution of the probability density of the state of a dynamical system given continuous-time observations. Building upon our recent work, we propose a new way to approximate the solution of the Kushner equation through tractable variational Gaussian approximations of two proximal losses associated with the propagation and Bayesian update of the probability density. The first is a proximal loss based on the Wasserstein metric and the second is a proximal loss based on the Fisher metric. The solution to this last proximal loss is given by implicit updates on the mean and covariance that we proposed earlier. These two variational updates can be fused and shown to satisfy a set of stochastic differential equations on the Gaussian's mean and covariance matrix. This Gaussian flow is consistent with the Kalman-Bucy and Riccati flows in the linear case and generalize them in the nonlinear one.

Multiple description video coding for real-time applications using HEVC

Remote control vehicles require the transmission of large amounts of data, and video is one of the most important sources for the driver. To ensure reliable video transmission, the encoded video stream is transmitted simultaneously over multiple channels. However, this solution incurs a high transmission cost due to the wireless channel's unreliable and random bit loss characteristics. To address this issue, it is necessary to use more efficient video encoding methods that can make the video stream robust to noise. In this paper, we propose a low-complexity, low-latency 2-channel Multiple Description Coding (MDC) solution with an adaptive Instantaneous Decoder Refresh (IDR) frame period, which is compatible with the HEVC standard. This method shows better resistance to high packet loss rates with lower complexity.

Variational inference via Wasserstein gradient flows

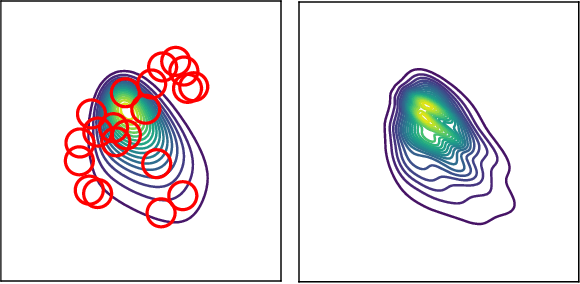
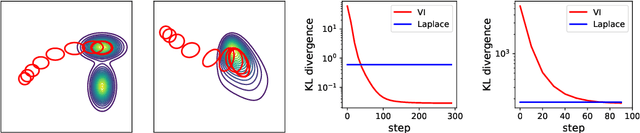
Along with Markov chain Monte Carlo (MCMC) methods, variational inference (VI) has emerged as a central computational approach to large-scale Bayesian inference. Rather than sampling from the true posterior $\pi$, VI aims at producing a simple but effective approximation $\hat \pi$ to $\pi$ for which summary statistics are easy to compute. However, unlike the well-studied MCMC methodology, VI is still poorly understood and dominated by heuristics. In this work, we propose principled methods for VI, in which $\hat \pi$ is taken to be a Gaussian or a mixture of Gaussians, which rest upon the theory of gradient flows on the Bures-Wasserstein space of Gaussian measures. Akin to MCMC, it comes with strong theoretical guarantees when $\pi$ is log-concave.