Efficiently learning depth-3 circuits via quantum agnostic boosting

We initiate the study of quantum agnostic learning of phase states with respect to a function class $\mathsf{C}\subseteq \{c:\{0,1\}^n\rightarrow \{0,1\}\}$: given copies of an unknown $n$-qubit state $|\psi\rangle$ which has fidelity $\textsf{opt}$ with a phase state $|\phi_c\rangle=\frac{1}{\sqrt{2^n}}\sum_{x\in \{0,1\}^n}(-1)^{c(x)}|x\rangle$ for some $c\in \mathsf{C}$, output $|\phi\rangle$ which has fidelity $|\langle \phi | \psi \rangle|^2 \geq \textsf{opt}-\varepsilon$. To this end, we give agnostic learning protocols for the following classes: (i) Size-$t$ decision trees which runs in time $\textsf{poly}(n,t,1/\varepsilon)$. This also implies $k$-juntas can be agnostically learned in time $\textsf{poly}(n,2^k,1/\varepsilon)$. (ii) $s$-term DNF formulas in near-polynomial time $\textsf{poly}(n,(s/\varepsilon)^{\log \log s/\varepsilon})$. Our main technical contribution is a quantum agnostic boosting protocol which converts a weak agnostic learner, which outputs a parity state $|\phi\rangle$ such that $|\langle \phi|\psi\rangle|^2\geq \textsf{opt}/\textsf{poly}(n)$, into a strong learner which outputs a superposition of parity states $|\phi'\rangle$ such that $|\langle \phi'|\psi\rangle|^2\geq \textsf{opt} - \varepsilon$. Using quantum agnostic boosting, we obtain the first near-polynomial time $n^{O(\log \log n)}$ algorithm for learning $\textsf{poly}(n)$-sized depth-$3$ circuits (consisting of $\textsf{AND}$, $\textsf{OR}$, $\textsf{NOT}$ gates) in the uniform quantum $\textsf{PAC}$ model using quantum examples. Classically, the analogue of efficient learning depth-$3$ circuits (and even depth-$2$ circuits) in the uniform $\textsf{PAC}$ model has been a longstanding open question in computational learning theory. Our work nearly settles this question, when the learner is given quantum examples.

Learning low-degree quantum objects

We consider the problem of learning low-degree quantum objects up to $\varepsilon$-error in $\ell_2$-distance. We show the following results: $(i)$ unknown $n$-qubit degree-$d$ (in the Pauli basis) quantum channels and unitaries can be learned using $O(1/\varepsilon^d)$ queries (independent of $n$), $(ii)$ polynomials $p:\{-1,1\}^n\rightarrow [-1,1]$ arising from $d$-query quantum algorithms can be classically learned from $O((1/\varepsilon)^d\cdot \log n)$ many random examples $(x,p(x))$ (which implies learnability even for $d=O(\log n)$), and $(iii)$ degree-$d$ polynomials $p:\{-1,1\}^n\to [-1,1]$ can be learned through $O(1/\varepsilon^d)$ queries to a quantum unitary $U_p$ that block-encodes $p$. Our main technical contributions are new Bohnenblust-Hille inequalities for quantum channels and completely bounded~polynomials.

Active Learning of Quantum System Hamiltonians yields Query Advantage

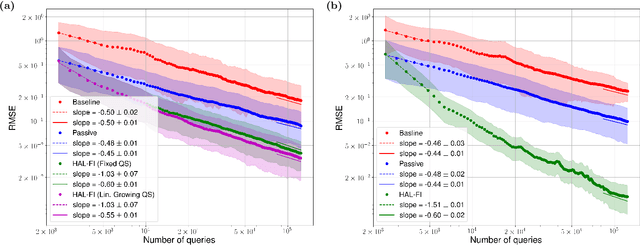
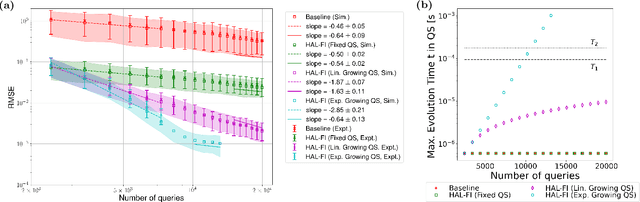
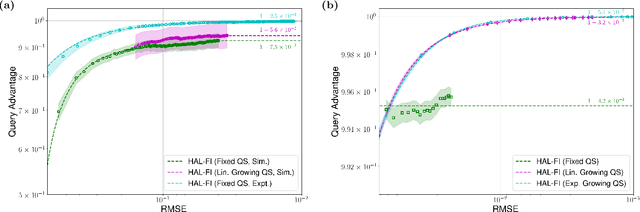
Hamiltonian learning is an important procedure in quantum system identification, calibration, and successful operation of quantum computers. Through queries to the quantum system, this procedure seeks to obtain the parameters of a given Hamiltonian model and description of noise sources. Standard techniques for Hamiltonian learning require careful design of queries and $O(\epsilon^{-2})$ queries in achieving learning error $\epsilon$ due to the standard quantum limit. With the goal of efficiently and accurately estimating the Hamiltonian parameters within learning error $\epsilon$ through minimal queries, we introduce an active learner that is given an initial set of training examples and the ability to interactively query the quantum system to generate new training data. We formally specify and experimentally assess the performance of this Hamiltonian active learning (HAL) algorithm for learning the six parameters of a two-qubit cross-resonance Hamiltonian on four different superconducting IBM Quantum devices. Compared with standard techniques for the same problem and a specified learning error, HAL achieves up to a $99.8\%$ reduction in queries required, and a $99.1\%$ reduction over the comparable non-adaptive learning algorithm. Moreover, with access to prior information on a subset of Hamiltonian parameters and given the ability to select queries with linearly (or exponentially) longer system interaction times during learning, HAL can exceed the standard quantum limit and achieve Heisenberg (or super-Heisenberg) limited convergence rates during learning.

Exponential Reduction in Sample Complexity with Learning of Ising Model Dynamics

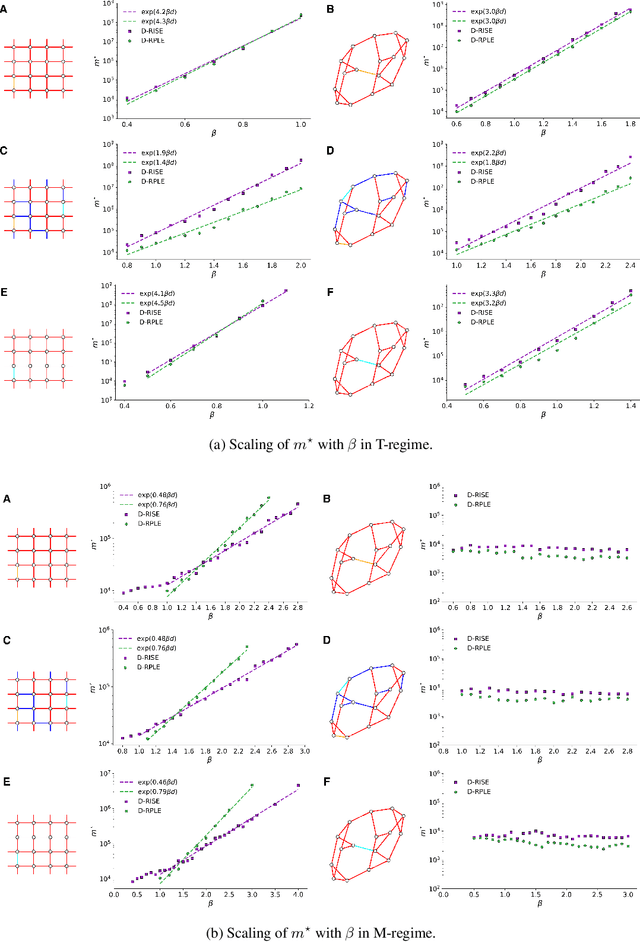
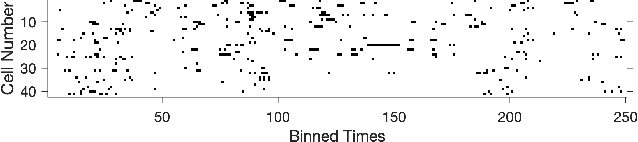
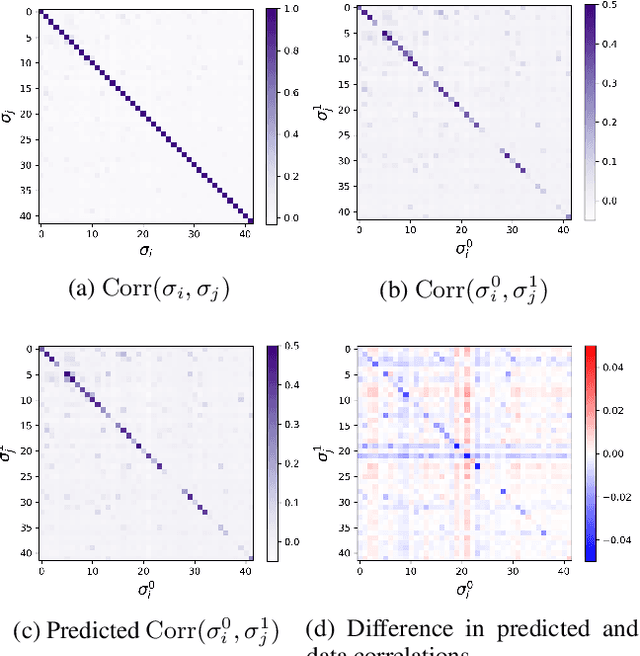
The usual setting for learning the structure and parameters of a graphical model assumes the availability of independent samples produced from the corresponding multivariate probability distribution. However, for many models the mixing time of the respective Markov chain can be very large and i.i.d. samples may not be obtained. We study the problem of reconstructing binary graphical models from correlated samples produced by a dynamical process, which is natural in many applications. We analyze the sample complexity of two estimators that are based on the interaction screening objective and the conditional likelihood loss. We observe that for samples coming from a dynamical process far from equilibrium, the sample complexity reduces exponentially compared to a dynamical process that mixes quickly.