Inpaint360GS: Efficient Object-Aware 3D Inpainting via Gaussian Splatting for 360° Scenes

Despite recent advances in single-object front-facing inpainting using NeRF and 3D Gaussian Splatting (3DGS), inpainting in complex 360° scenes remains largely underexplored. This is primarily due to three key challenges: (i) identifying target objects in the 3D field of 360° environments, (ii) dealing with severe occlusions in multi-object scenes, which makes it hard to define regions to inpaint, and (iii) maintaining consistent and high-quality appearance across views effectively. To tackle these challenges, we propose Inpaint360GS, a flexible 360° editing framework based on 3DGS that supports multi-object removal and high-fidelity inpainting in 3D space. By distilling 2D segmentation into 3D and leveraging virtual camera views for contextual guidance, our method enables accurate object-level editing and consistent scene completion. We further introduce a new dataset tailored for 360° inpainting, addressing the lack of ground truth object-free scenes. Experiments demonstrate that Inpaint360GS outperforms existing baselines and achieves state-of-the-art performance. Project page: https://dfki-av.github.io/inpaint360gs/

MRF-PINN: A Multi-Receptive-Field convolutional physics-informed neural network for solving partial differential equations

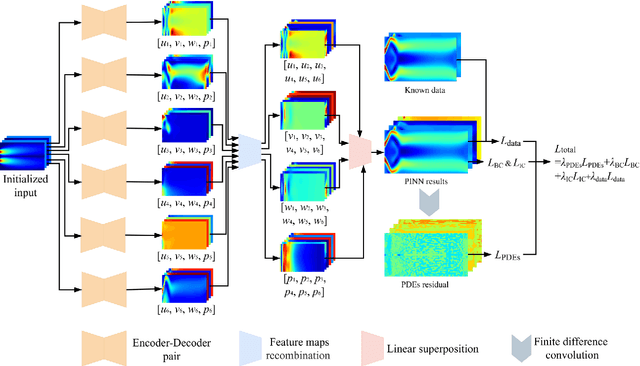
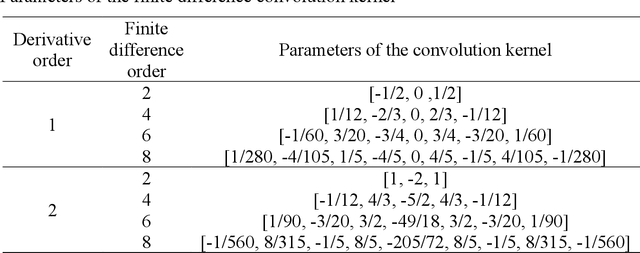
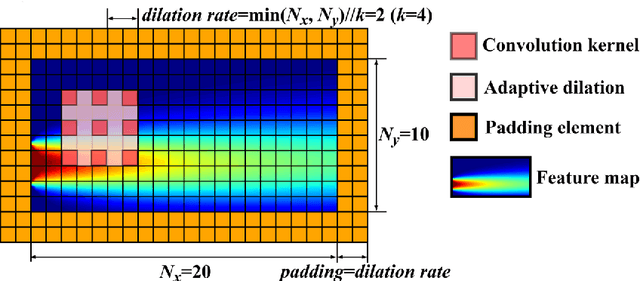
Compared with conventional numerical approaches to solving partial differential equations (PDEs), physics-informed neural networks (PINN) have manifested the capability to save development effort and computational cost, especially in scenarios of reconstructing the physics field and solving the inverse problem. Considering the advantages of parameter sharing, spatial feature extraction and low inference cost, convolutional neural networks (CNN) are increasingly used in PINN. However, some challenges still remain as follows. To adapt convolutional PINN to solve different PDEs, considerable effort is usually needed for tuning critical hyperparameters. Furthermore, the effects of the finite difference accuracy, and the mesh resolution on the predictivity of convolutional PINN are not settled. To fill the gaps above, we propose three initiatives in this paper: (1) A Multi-Receptive-Field PINN (MRF-PINN) model is established to solve different types of PDEs on various mesh resolutions without manual tuning; (2) The dimensional balance method is used to estimate the loss weights when solving Navier-Stokes equations; (3) The Taylor polynomial is used to pad the virtual nodes near the boundaries for implementing high-order finite difference. The proposed MRF-PINN is tested for solving three typical linear PDEs (elliptic, parabolic, hyperbolic) and a series of nonlinear PDEs (Navier-Stokes PDEs) to demonstrate its generality and superiority. This paper shows that MRF-PINN can adapt to completely different equation types and mesh resolutions without any hyperparameter tuning. The dimensional balance method saves computational time and improves the convergence for solving Navier-Stokes PDEs. Further, the solving error is significantly decreased under high-order finite difference, large channel number, and high mesh resolution, which is expected to be a general convolutional PINN scheme.