Calibrated Predictive Lower Bounds on Time-to-Unsafe-Sampling in LLMs

We develop a framework to quantify the time-to-unsafe-sampling - the number of large language model (LLM) generations required to trigger an unsafe (e.g., toxic) response. Estimating this quantity is challenging, since unsafe responses are exceedingly rare in well-aligned LLMs, potentially occurring only once in thousands of generations. As a result, directly estimating time-to-unsafe-sampling would require collecting training data with a prohibitively large number of generations per prompt. However, with realistic sampling budgets, we often cannot generate enough responses to observe an unsafe outcome for every prompt, leaving the time-to-unsafe-sampling unobserved in many cases, making the estimation and evaluation tasks particularly challenging. To address this, we frame this estimation problem as one of survival analysis and develop a provably calibrated lower predictive bound (LPB) on the time-to-unsafe-sampling of a given prompt, leveraging recent advances in conformal prediction. Our key innovation is designing an adaptive, per-prompt sampling strategy, formulated as a convex optimization problem. The objective function guiding this optimized sampling allocation is designed to reduce the variance of the estimators used to construct the LPB, leading to improved statistical efficiency over naive methods that use a fixed sampling budget per prompt. Experiments on both synthetic and real data support our theoretical results and demonstrate the practical utility of our method for safety risk assessment in generative AI models.

Conformal Prediction with Corrupted Labels: Uncertain Imputation and Robust Re-weighting

We introduce a framework for robust uncertainty quantification in situations where labeled training data are corrupted, through noisy or missing labels. We build on conformal prediction, a statistical tool for generating prediction sets that cover the test label with a pre-specified probability. The validity of conformal prediction, however, holds under the i.i.d assumption, which does not hold in our setting due to the corruptions in the data. To account for this distribution shift, the privileged conformal prediction (PCP) method proposed leveraging privileged information (PI) -- additional features available only during training -- to re-weight the data distribution, yielding valid prediction sets under the assumption that the weights are accurate. In this work, we analyze the robustness of PCP to inaccuracies in the weights. Our analysis indicates that PCP can still yield valid uncertainty estimates even when the weights are poorly estimated. Furthermore, we introduce uncertain imputation (UI), a new conformal method that does not rely on weight estimation. Instead, we impute corrupted labels in a way that preserves their uncertainty. Our approach is supported by theoretical guarantees and validated empirically on both synthetic and real benchmarks. Finally, we show that these techniques can be integrated into a triply robust framework, ensuring statistically valid predictions as long as at least one underlying method is valid.

Robust Conformal Prediction Using Privileged Information

We develop a method to generate prediction sets with a guaranteed coverage rate that is robust to corruptions in the training data, such as missing or noisy variables. Our approach builds on conformal prediction, a powerful framework to construct prediction sets that are valid under the i.i.d assumption. Importantly, naively applying conformal prediction does not provide reliable predictions in this setting, due to the distribution shift induced by the corruptions. To account for the distribution shift, we assume access to privileged information (PI). The PI is formulated as additional features that explain the distribution shift, however, they are only available during training and absent at test time. We approach this problem by introducing a novel generalization of weighted conformal prediction and support our method with theoretical coverage guarantees. Empirical experiments on both real and synthetic datasets indicate that our approach achieves a valid coverage rate and constructs more informative predictions compared to existing methods, which are not supported by theoretical guarantees.

Conformalized Online Learning: Online Calibration Without a Holdout Set

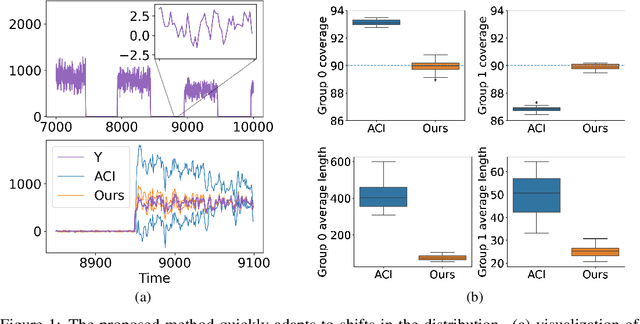
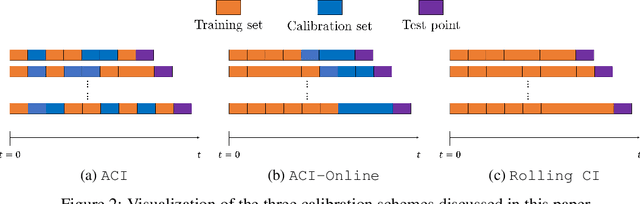
We develop a framework for constructing uncertainty sets with a valid coverage guarantee in an online setting, in which the underlying data distribution can drastically -- and even adversarially -- shift over time. The technique we propose is highly flexible as it can be integrated with any online learning algorithm, requiring minimal implementation effort and computational cost. A key advantage of our method over existing alternatives -- which also build on conformal inference -- is that we do not need to split the data into training and holdout calibration sets. This allows us to fit the predictive model in a fully online manner, utilizing the most recent observation for constructing calibrated uncertainty sets. Consequently, and in contrast with existing techniques, (i) the sets we build can quickly adapt to new changes in the distribution; and (ii) our procedure does not require refitting the model at each time step. Using synthetic and real-world benchmark data sets, we demonstrate the validity of our theory and the improved performance of our proposal over existing techniques. To demonstrate the greater flexibility of the proposed method, we show how to construct valid intervals for a multiple-output regression problem that previous sequential calibration methods cannot handle due to impractical computational and memory requirements.

Weisfeiler and Leman Go Infinite: Spectral and Combinatorial Pre-Colorings

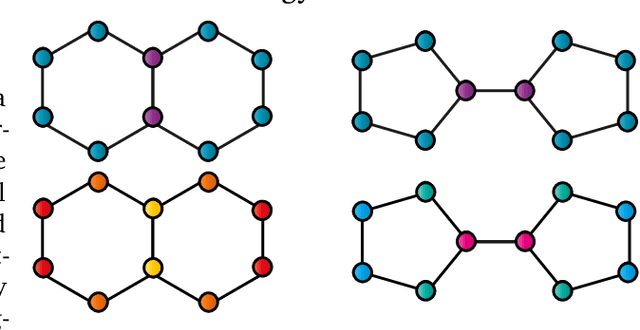
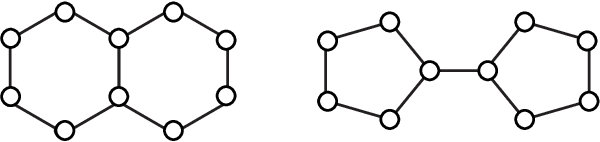
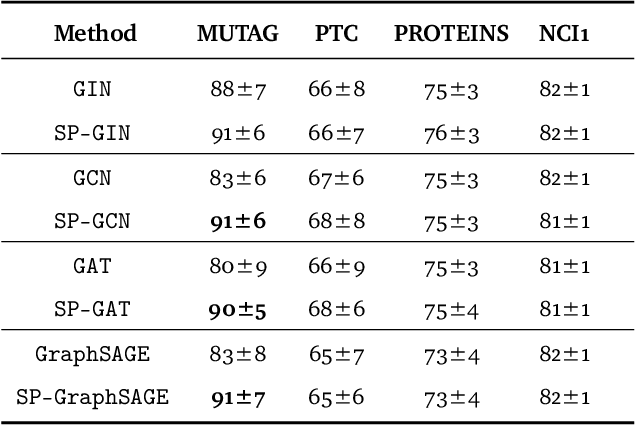
Graph isomorphism testing is usually approached via the comparison of graph invariants. Two popular alternatives that offer a good trade-off between expressive power and computational efficiency are combinatorial (i.e., obtained via the Weisfeiler-Leman (WL) test) and spectral invariants. While the exact power of the latter is still an open question, the former is regularly criticized for its limited power, when a standard configuration of uniform pre-coloring is used. This drawback hinders the applicability of Message Passing Graph Neural Networks (MPGNNs), whose expressive power is upper bounded by the WL test. Relaxing the assumption of uniform pre-coloring, we show that one can increase the expressive power of the WL test ad infinitum. Following that, we propose an efficient pre-coloring based on spectral features that provably increase the expressive power of the vanilla WL test. The above claims are accompanied by extensive synthetic and real data experiments. The code to reproduce our experiments is available at https://github.com/TPFI22/Spectral-and-Combinatorial

Calibrated Multiple-Output Quantile Regression with Representation Learning

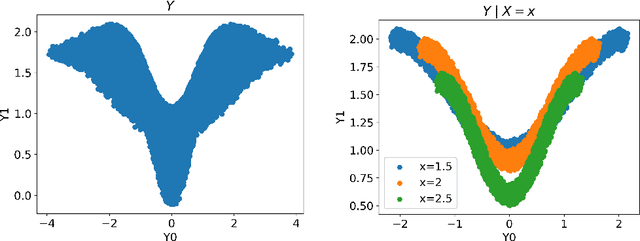
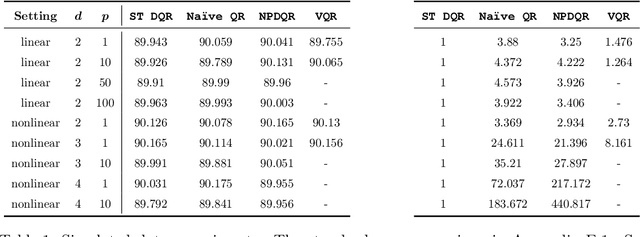
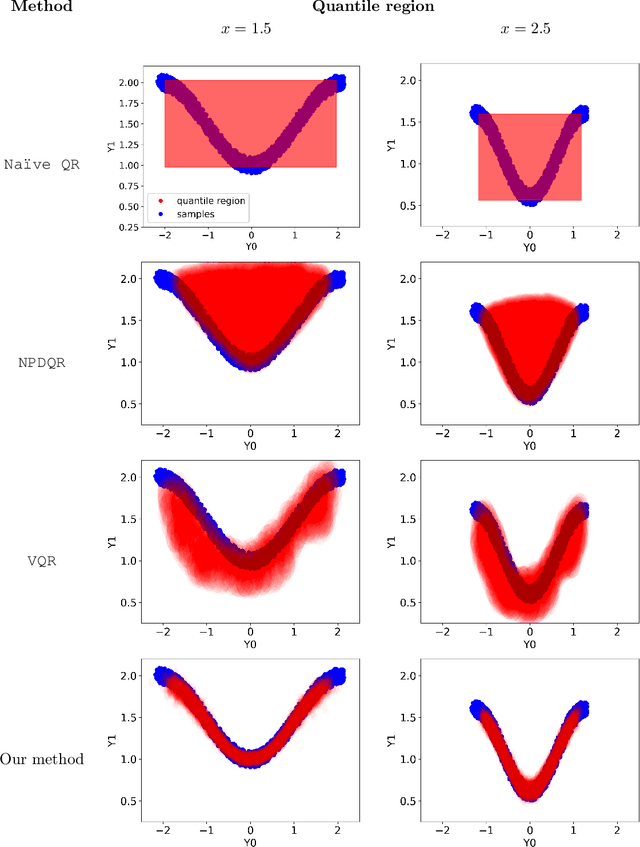
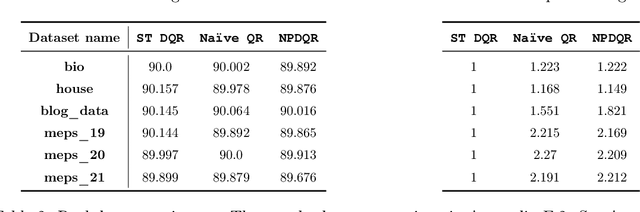
We develop a method to generate predictive regions that cover a multivariate response variable with a user-specified probability. Our work is composed of two components. First, we use a deep generative model to learn a representation of the response that has a unimodal distribution. Existing multiple-output quantile regression approaches are effective in such cases, so we apply them on the learned representation, and then transform the solution to the original space of the response. This process results in a flexible and informative region that can have an arbitrary shape, a property that existing methods lack. Second, we propose an extension of conformal prediction to the multivariate response setting that modifies any method to return sets with a pre-specified coverage level. The desired coverage is theoretically guaranteed in the finite-sample case for any distribution. Experiments conducted on both real and synthetic data show that our method constructs regions that are significantly smaller (sometimes by a factor of 100) compared to existing techniques.

Improving Conditional Coverage via Orthogonal Quantile Regression

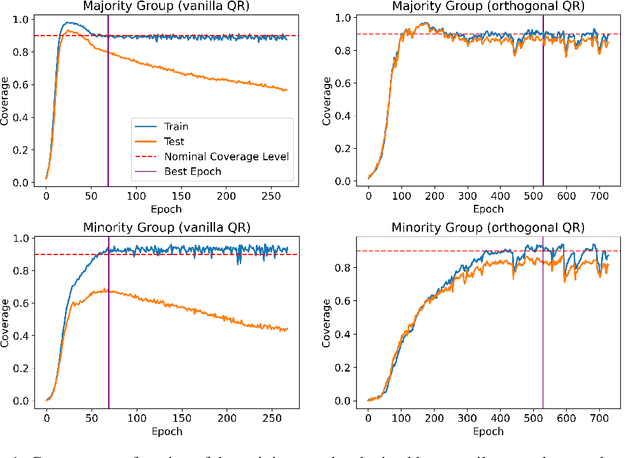
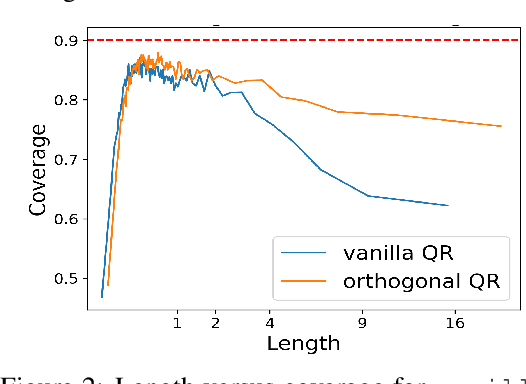
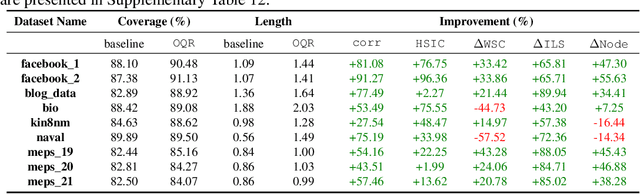
We develop a method to generate prediction intervals that have a user-specified coverage level across all regions of feature-space, a property called conditional coverage. A typical approach to this task is to estimate the conditional quantiles with quantile regression -- it is well-known that this leads to correct coverage in the large-sample limit, although it may not be accurate in finite samples. We find in experiments that traditional quantile regression can have poor conditional coverage. To remedy this, we modify the loss function to promote independence between the size of the intervals and the indicator of a miscoverage event. For the true conditional quantiles, these two quantities are independent (orthogonal), so the modified loss function continues to be valid. Moreover, we empirically show that the modified loss function leads to improved conditional coverage, as evaluated by several metrics. We also introduce two new metrics that check conditional coverage by looking at the strength of the dependence between the interval size and the indicator of miscoverage.