An Online Feasible Point Method for Benign Generalized Nash Equilibrium Problems

We consider a repeatedly played generalized Nash equilibrium game. This induces a multi-agent online learning problem with joint constraints. An important challenge in this setting is that the feasible set for each agent depends on the simultaneous moves of the other agents and, therefore, varies over time. As a consequence, the agents face time-varying constraints, which are not adversarial but rather endogenous to the system. Prior work in this setting focused on convergence to a feasible solution in the limit via integrating the constraints in the objective as a penalty function. However, no existing work can guarantee that the constraints are satisfied for all iterations while simultaneously guaranteeing convergence to a generalized Nash equilibrium. This is a problem of fundamental theoretical interest and practical relevance. In this work, we introduce a new online feasible point method. Under the assumption that limited communication between the agents is allowed, this method guarantees feasibility. We identify the class of benign generalized Nash equilibrium problems, for which the convergence of our method to the equilibrium is guaranteed. We set this class of benign generalized Nash equilibrium games in context with existing definitions and illustrate our method with examples.

Tracking solutions of time-varying variational inequalities

Tracking the solution of time-varying variational inequalities is an important problem with applications in game theory, optimization, and machine learning. Existing work considers time-varying games or time-varying optimization problems. For strongly convex optimization problems or strongly monotone games, these results provide tracking guarantees under the assumption that the variation of the time-varying problem is restrained, that is, problems with a sublinear solution path. In this work we extend existing results in two ways: In our first result, we provide tracking bounds for (1) variational inequalities with a sublinear solution path but not necessarily monotone functions, and (2) for periodic time-varying variational inequalities that do not necessarily have a sublinear solution path-length. Our second main contribution is an extensive study of the convergence behavior and trajectory of discrete dynamical systems of periodic time-varying VI. We show that these systems can exhibit provably chaotic behavior or can converge to the solution. Finally, we illustrate our theoretical results with experiments.

Generalization Guarantees via Algorithm-dependent Rademacher Complexity

Algorithm- and data-dependent generalization bounds are required to explain the generalization behavior of modern machine learning algorithms. In this context, there exists information theoretic generalization bounds that involve (various forms of) mutual information, as well as bounds based on hypothesis set stability. We propose a conceptually related, but technically distinct complexity measure to control generalization error, which is the empirical Rademacher complexity of an algorithm- and data-dependent hypothesis class. Combining standard properties of Rademacher complexity with the convenient structure of this class, we are able to (i) obtain novel bounds based on the finite fractal dimension, which (a) extend previous fractal dimension-type bounds from continuous to finite hypothesis classes, and (b) avoid a mutual information term that was required in prior work; (ii) we greatly simplify the proof of a recent dimension-independent generalization bound for stochastic gradient descent; and (iii) we easily recover results for VC classes and compression schemes, similar to approaches based on conditional mutual information.

Towards Characterizing the First-order Query Complexity of Learning (Approximate) Nash Equilibria in Zero-sum Matrix Games

In the first-order query model for zero-sum $K\times K$ matrix games, playersobserve the expected pay-offs for all their possible actions under therandomized action played by their opponent. This is a classical model,which has received renewed interest after the discoveryby Rakhlin and Sridharan that $\epsilon$-approximate Nash equilibria can be computedefficiently from $O(\ln K / \epsilon) $ instead of $O( \ln K / \epsilon^2)$ queries.Surprisingly, the optimal number of such queries, as a function of both$\epsilon$ and $K$, is not known.We make progress on this question on two fronts. First, we fully characterise the query complexity of learning exact equilibria ($\epsilon=0$), by showing that they require a number of queries that is linearin $K$, which means that it is essentially as hard as querying the wholematrix, which can also be done with $K$ queries. Second, for $\epsilon > 0$, the currentquery complexity upper bound stands at $O(\min(\ln(K) / \epsilon , K))$. We argue that, unfortunately, obtaining matchinglower bound is not possible with existing techniques: we prove that nolower bound can be derived by constructing hard matrices whose entriestake values in a known countable set, because such matrices can be fullyidentified by a single query. This rules out, for instance, reducing toa submodular optimization problem over the hypercube by encoding itas a binary matrix. We then introduce a new technique for lower bounds,which allows us to obtain lower bounds of order$\tilde\Omega(\log(1 / (K\epsilon)))$ for any $\epsilon \leq1 / cK^4$, where $c$ is a constant independent of $K$. We furtherdiscuss possible future directions to improve on our techniques in orderto close the gap with the upper bounds.

Accelerated Rates between Stochastic and Adversarial Online Convex Optimization

Stochastic and adversarial data are two widely studied settings in online learning. But many optimization tasks are neither i.i.d. nor fully adversarial, which makes it of fundamental interest to get a better theoretical understanding of the world between these extremes. In this work we establish novel regret bounds for online convex optimization in a setting that interpolates between stochastic i.i.d. and fully adversarial losses. By exploiting smoothness of the expected losses, these bounds replace a dependence on the maximum gradient length by the variance of the gradients, which was previously known only for linear losses. In addition, they weaken the i.i.d. assumption by allowing, for example, adversarially poisoned rounds, which were previously considered in the related expert and bandit settings. In the fully i.i.d. case, our regret bounds match the rates one would expect from results in stochastic acceleration, and we also recover the optimal stochastically accelerated rates via online-to-batch conversion. In the fully adversarial case our bounds gracefully deteriorate to match the minimax regret. We further provide lower bounds showing that our regret upper bounds are tight for all intermediate regimes in terms of the stochastic variance and the adversarial variation of the loss gradients.

Between Stochastic and Adversarial Online Convex Optimization: Improved Regret Bounds via Smoothness

Stochastic and adversarial data are two widely studied settings in online learning. But many optimization tasks are neither i.i.d. nor fully adversarial, which makes it of fundamental interest to get a better theoretical understanding of the world between these extremes. In this work we establish novel regret bounds for online convex optimization in a setting that interpolates between stochastic i.i.d. and fully adversarial losses. By exploiting smoothness of the expected losses, these bounds replace a dependence on the maximum gradient length by the variance of the gradients, which was previously known only for linear losses. In addition, they weaken the i.i.d. assumption by allowing adversarially poisoned rounds or shifts in the data distribution. To accomplish this goal, we introduce two key quantities associated with the loss sequence, that we call the cumulative stochastic variance and the adversarial variation. Our upper bounds are attained by instances of optimistic follow the regularized leader, and we design adaptive learning rates that automatically adapt to the cumulative stochastic variance and adversarial variation. In the fully i.i.d. case, our bounds match the rates one would expect from results in stochastic acceleration, and in the fully adversarial case they gracefully deteriorate to match the minimax regret. We further provide lower bounds showing that our regret upper bounds are tight for all intermediate regimes for the cumulative stochastic variance and the adversarial variation.

Robust Online Convex Optimization in the Presence of Outliers

We consider online convex optimization when a number k of data points are outliers that may be corrupted. We model this by introducing the notion of robust regret, which measures the regret only on rounds that are not outliers. The aim for the learner is to achieve small robust regret, without knowing where the outliers are. If the outliers are chosen adversarially, we show that a simple filtering strategy on extreme gradients incurs O(k) additive overhead compared to the usual regret bounds, and that this is unimprovable, which means that k needs to be sublinear in the number of rounds. We further ask which additional assumptions would allow for a linear number of outliers. It turns out that the usual benign cases of independently, identically distributed (i.i.d.) observations or strongly convex losses are not sufficient. However, combining i.i.d. observations with the assumption that outliers are those observations that are in an extreme quantile of the distribution, does lead to sublinear robust regret, even though the expected number of outliers is linear.

A Century of Portraits: A Visual Historical Record of American High School Yearbooks

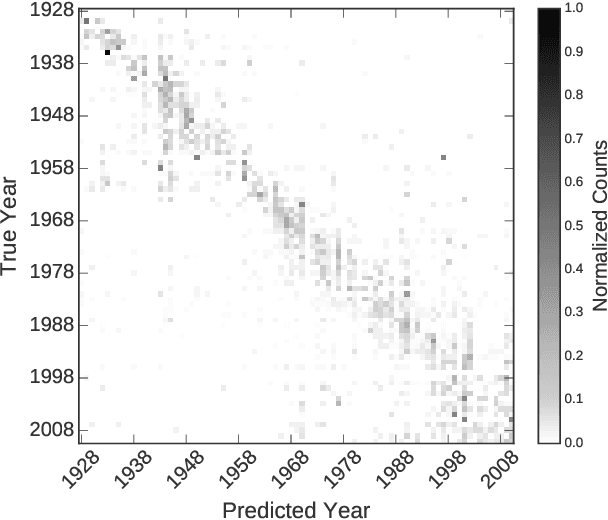
Many details about our world are not captured in written records because they are too mundane or too abstract to describe in words. Fortunately, since the invention of the camera, an ever-increasing number of photographs capture much of this otherwise lost information. This plethora of artifacts documenting our "visual culture" is a treasure trove of knowledge as yet untapped by historians. We present a dataset of 37,921 frontal-facing American high school yearbook photos that allow us to use computation to glimpse into the historical visual record too voluminous to be evaluated manually. The collected portraits provide a constant visual frame of reference with varying content. We can therefore use them to consider issues such as a decade's defining style elements, or trends in fashion and social norms over time. We demonstrate that our historical image dataset may be used together with weakly-supervised data-driven techniques to perform scalable historical analysis of large image corpora with minimal human effort, much in the same way that large text corpora together with natural language processing revolutionized historians' workflow. Furthermore, we demonstrate the use of our dataset in dating grayscale portraits using deep learning methods.