VeriCoT: Neuro-symbolic Chain-of-Thought Validation via Logical Consistency Checks

LLMs can perform multi-step reasoning through Chain-of-Thought (CoT), but they cannot reliably verify their own logic. Even when they reach correct answers, the underlying reasoning may be flawed, undermining trust in high-stakes scenarios. To mitigate this issue, we introduce VeriCoT, a neuro-symbolic method that extracts and verifies formal logical arguments from CoT reasoning. VeriCoT formalizes each CoT reasoning step into first-order logic and identifies premises that ground the argument in source context, commonsense knowledge, or prior reasoning steps. The symbolic representation enables automated solvers to verify logical validity while the NL premises allow humans and systems to identify ungrounded or fallacious reasoning steps. Experiments on the ProofWriter, LegalBench, and BioASQ datasets show VeriCoT effectively identifies flawed reasoning, and serves as a strong predictor of final answer correctness. We also leverage VeriCoT's verification signal for (1) inference-time self-reflection, (2) supervised fine-tuning (SFT) on VeriCoT-distilled datasets and (3) preference fine-tuning (PFT) with direct preference optimization (DPO) using verification-based pairwise rewards, further improving reasoning validity and accuracy.

Teaching Large Language Models to Reason through Learning and Forgetting

Leveraging inference-time search in large language models has proven effective in further enhancing a trained model's capability to solve complex mathematical and reasoning problems. However, this approach significantly increases computational costs and inference time, as the model must generate and evaluate multiple candidate solutions to identify a viable reasoning path. To address this, we propose an effective approach that integrates search capabilities directly into the model by fine-tuning it using both successful (learning) and failed reasoning paths (forgetting) derived from diverse search methods. While fine-tuning the model with these data might seem straightforward, we identify a critical issue: the model's search capability tends to degrade rapidly if fine-tuning is performed naively. We show that this degradation can be substantially mitigated by employing a smaller learning rate. Extensive experiments on the challenging Game-of-24 and Countdown mathematical reasoning benchmarks show that our approach not only outperforms both standard fine-tuning and inference-time search baselines but also significantly reduces inference time by 180$\times$.

Risk-Averse Finetuning of Large Language Models

We consider the challenge of mitigating the generation of negative or toxic content by the Large Language Models (LLMs) in response to certain prompts. We propose integrating risk-averse principles into LLM fine-tuning to minimize the occurrence of harmful outputs, particularly rare but significant events. By optimizing the risk measure of Conditional Value at Risk (CVaR), our methodology trains LLMs to exhibit superior performance in avoiding toxic outputs while maintaining effectiveness in generative tasks. Empirical evaluations on sentiment modification and toxicity mitigation tasks demonstrate the efficacy of risk-averse reinforcement learning with human feedback (RLHF) in promoting a safer and more constructive online discourse environment.

AgentOccam: A Simple Yet Strong Baseline for LLM-Based Web Agents

Autonomy via agents using large language models (LLMs) for personalized, standardized tasks boosts human efficiency. Automating web tasks (like booking hotels within a budget) is increasingly sought after. Fulfilling practical needs, the web agent also serves as an important proof-of-concept example for various agent grounding scenarios, with its success promising advancements in many future applications. Prior research often handcrafts web agent strategies (e.g., prompting templates, multi-agent systems, search methods, etc.) and the corresponding in-context examples, which may not generalize well across all real-world scenarios. On the other hand, there has been limited study on the misalignment between a web agent's observation/action representation and the pre-training data of the LLM it's based on. This discrepancy is especially notable when LLMs are primarily trained for language completion rather than tasks involving embodied navigation actions and symbolic web elements. Our study enhances an LLM-based web agent by simply refining its observation and action space to better align with the LLM's capabilities. This approach enables our base agent to significantly outperform previous methods on a wide variety of web tasks. Specifically, on WebArena, a benchmark featuring general-purpose web interaction tasks, our agent AgentOccam surpasses the previous state-of-the-art and concurrent work by 9.8 (+29.4%) and 5.9 (+15.8%) absolute points respectively, and boosts the success rate by 26.6 points (+161%) over similar plain web agents with its observation and action space alignment. We achieve this without using in-context examples, new agent roles, online feedback or search strategies. AgentOccam's simple design highlights LLMs' impressive zero-shot performance on web tasks, and underlines the critical role of carefully tuning observation and action spaces for LLM-based agents.

Pedagogical Alignment of Large Language Models

In this paper, we introduce the novel concept of pedagogically aligned Large Language Models (LLMs) that signifies a transformative shift in the application of LLMs within educational contexts. Rather than providing direct responses to user queries, pedagogically-aligned LLMs function as scaffolding tools, breaking complex problems into manageable subproblems and guiding students towards the final answer through constructive feedback and hints. The objective is to equip learners with problem-solving strategies that deepen their understanding and internalization of the subject matter. Previous research in this field has primarily applied the supervised finetuning approach without framing the objective as an alignment problem, hence not employing reinforcement learning through human feedback (RLHF) methods. This study reinterprets the narrative by viewing the task through the lens of alignment and demonstrates how RLHF methods emerge naturally as a superior alternative for aligning LLM behaviour. Building on this perspective, we propose a novel approach for constructing a reward dataset specifically designed for the pedagogical alignment of LLMs. We apply three state-of-the-art RLHF algorithms and find that they outperform SFT significantly. Our qualitative analyses across model differences and hyperparameter sensitivity further validate the superiority of RLHF over SFT. Also, our study sheds light on the potential of online feedback for enhancing the performance of pedagogically-aligned LLMs, thus providing valuable insights for the advancement of these models in educational settings.

Dynamic Regret Analysis of Safe Distributed Online Optimization for Convex and Non-convex Problems

This paper addresses safe distributed online optimization over an unknown set of linear safety constraints. A network of agents aims at jointly minimizing a global, time-varying function, which is only partially observable to each individual agent. Therefore, agents must engage in local communications to generate a safe sequence of actions competitive with the best minimizer sequence in hindsight, and the gap between the two sequences is quantified via dynamic regret. We propose distributed safe online gradient descent (D-Safe-OGD) with an exploration phase, where all agents estimate the constraint parameters collaboratively to build estimated feasible sets, ensuring the action selection safety during the optimization phase. We prove that for convex functions, D-Safe-OGD achieves a dynamic regret bound of $O(T^{2/3} \sqrt{\log T} + T^{1/3}C_T^*)$, where $C_T^*$ denotes the path-length of the best minimizer sequence. We further prove a dynamic regret bound of $O(T^{2/3} \sqrt{\log T} + T^{2/3}C_T^*)$ for certain non-convex problems, which establishes the first dynamic regret bound for a safe distributed algorithm in the non-convex setting.

Enhanced Meta Reinforcement Learning using Demonstrations in Sparse Reward Environments

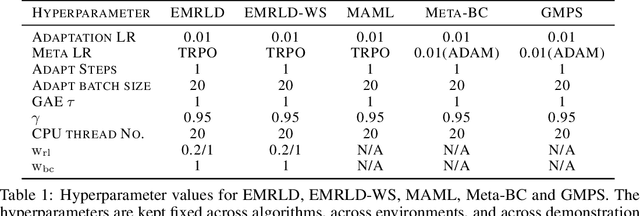
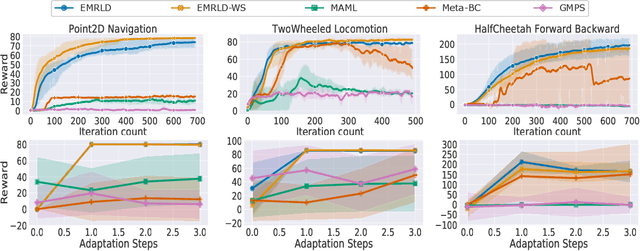
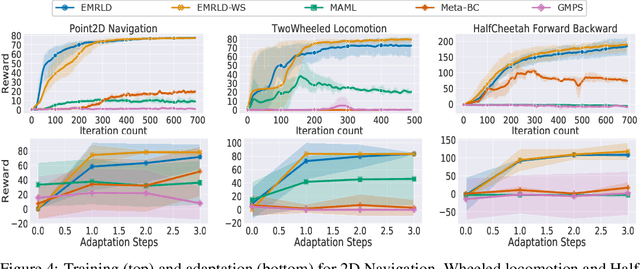
Meta reinforcement learning (Meta-RL) is an approach wherein the experience gained from solving a variety of tasks is distilled into a meta-policy. The meta-policy, when adapted over only a small (or just a single) number of steps, is able to perform near-optimally on a new, related task. However, a major challenge to adopting this approach to solve real-world problems is that they are often associated with sparse reward functions that only indicate whether a task is completed partially or fully. We consider the situation where some data, possibly generated by a sub-optimal agent, is available for each task. We then develop a class of algorithms entitled Enhanced Meta-RL using Demonstrations (EMRLD) that exploit this information even if sub-optimal to obtain guidance during training. We show how EMRLD jointly utilizes RL and supervised learning over the offline data to generate a meta-policy that demonstrates monotone performance improvements. We also develop a warm started variant called EMRLD-WS that is particularly efficient for sub-optimal demonstration data. Finally, we show that our EMRLD algorithms significantly outperform existing approaches in a variety of sparse reward environments, including that of a mobile robot.

Safe Online Convex Optimization with Unknown Linear Safety Constraints

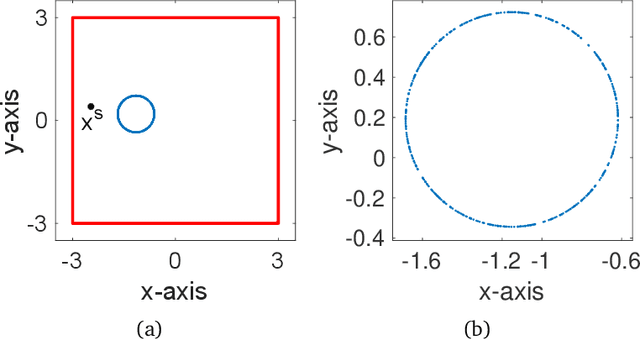
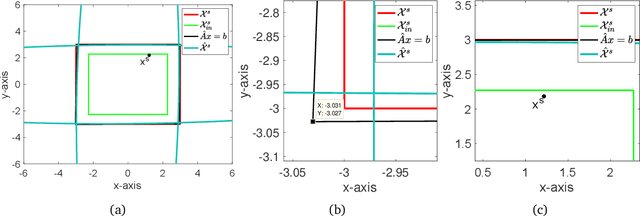
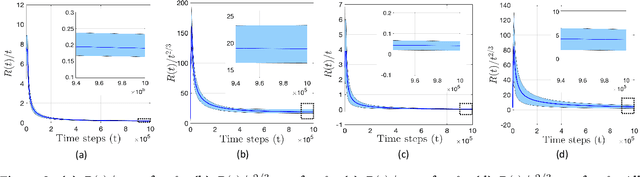
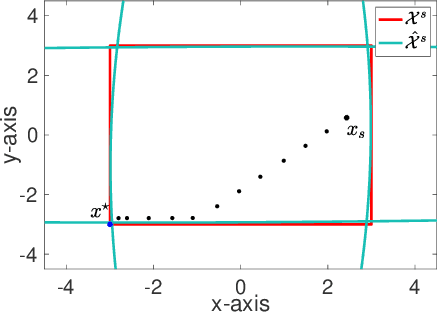
We study the problem of safe online convex optimization, where the action at each time step must satisfy a set of linear safety constraints. The goal is to select a sequence of actions to minimize the regret without violating the safety constraints at any time step (with high probability). The parameters that specify the linear safety constraints are unknown to the algorithm. The algorithm has access to only the noisy observations of constraints for the chosen actions. We propose an algorithm, called the {Safe Online Projected Gradient Descent} (SO-PGD) algorithm, to address this problem. We show that, under the assumption of the availability of a safe baseline action, the SO-PGD algorithm achieves a regret $O(T^{2/3})$. While there are many algorithms for online convex optimization (OCO) problems with safety constraints available in the literature, they allow constraint violations during learning/optimization, and the focus has been on characterizing the cumulative constraint violations. To the best of our knowledge, ours is the first work that provides an algorithm with provable guarantees on the regret, without violating the linear safety constraints (with high probability) at any time step.

Smooth Imitation Learning via Smooth Costs and Smooth Policies

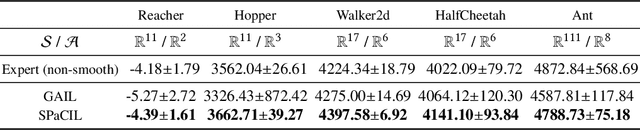
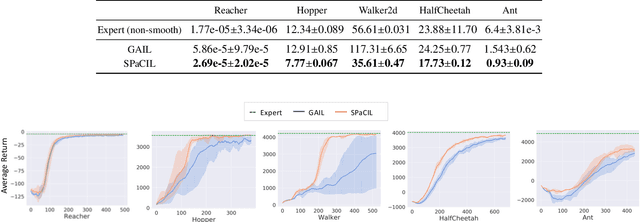
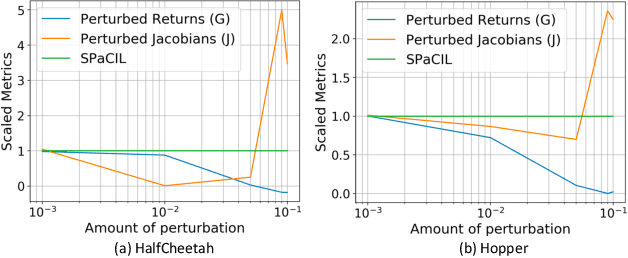
Imitation learning (IL) is a popular approach in the continuous control setting as among other reasons it circumvents the problems of reward mis-specification and exploration in reinforcement learning (RL). In IL from demonstrations, an important challenge is to obtain agent policies that are smooth with respect to the inputs. Learning through imitation a policy that is smooth as a function of a large state-action ($s$-$a$) space (typical of high dimensional continuous control environments) can be challenging. We take a first step towards tackling this issue by using smoothness inducing regularizers on \textit{both} the policy and the cost models of adversarial imitation learning. Our regularizers work by ensuring that the cost function changes in a controlled manner as a function of $s$-$a$ space; and the agent policy is well behaved with respect to the state space. We call our new smooth IL algorithm \textit{Smooth Policy and Cost Imitation Learning} (SPaCIL, pronounced 'Special'). We introduce a novel metric to quantify the smoothness of the learned policies. We demonstrate SPaCIL's superior performance on continuous control tasks from MuJoCo. The algorithm not just outperforms the state-of-the-art IL algorithm on our proposed smoothness metric, but, enjoys added benefits of faster learning and substantially higher average return.