Harnessing the Power of Infinitely Wide Deep Nets on Small-data Tasks

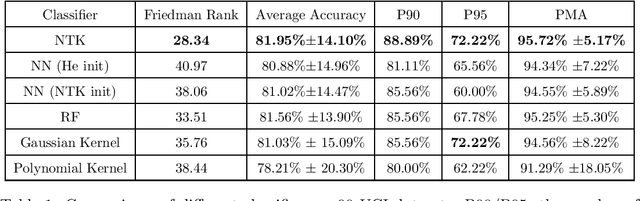
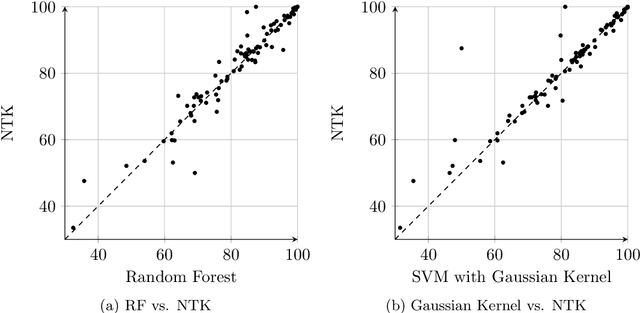
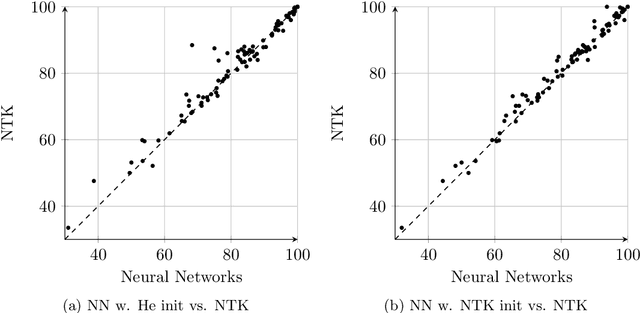
Recent research shows that the following two models are equivalent: (a) infinitely wide neural networks (NNs) trained under l2 loss by gradient descent with infinitesimally small learning rate (b) kernel regression with respect to so-called Neural Tangent Kernels (NTKs) (Jacot et al., 2018). An efficient algorithm to compute the NTK, as well as its convolutional counterparts, appears in Arora et al. (2019a), which allowed studying performance of infinitely wide nets on datasets like CIFAR-10. However, super-quadratic running time of kernel methods makes them best suited for small-data tasks. We report results suggesting neural tangent kernels perform strongly on low-data tasks. 1. On a standard testbed of classification/regression tasks from the UCI database, NTK SVM beats the previous gold standard, Random Forests (RF), and also the corresponding finite nets. 2. On CIFAR-10 with 10 - 640 training samples, Convolutional NTK consistently beats ResNet-34 by 1% - 3%. 3. On VOC07 testbed for few-shot image classification tasks on ImageNet with transfer learning (Goyal et al., 2019), replacing the linear SVM currently used with a Convolutional NTK SVM consistently improves performance. 4. Comparing the performance of NTK with the finite-width net it was derived from, NTK behavior starts at lower net widths than suggested by theoretical analysis(Arora et al., 2019a). NTK's efficacy may trace to lower variance of output.

Explaining Landscape Connectivity of Low-cost Solutions for Multilayer Nets

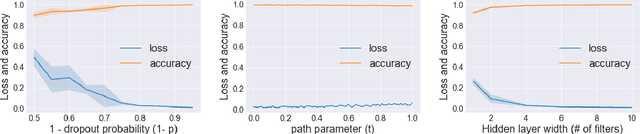
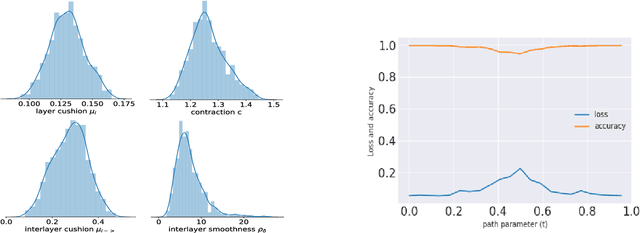
Mode connectivity is a surprising phenomenon in the loss landscape of deep nets. Optima---at least those discovered by gradient-based optimization---turn out to be connected by simple paths on which the loss function is almost constant. Often, these paths can be chosen to be piece-wise linear, with as few as two segments. We give mathematical explanations for this phenomenon, assuming generic properties (such as dropout stability and noise stability) of well-trained deep nets, which have previously been identified as part of understanding the generalization properties of deep nets. Our explanation holds for realistic multilayer nets, and experiments are presented to verify the theory.

A Simple Saliency Method That Passes the Sanity Checks

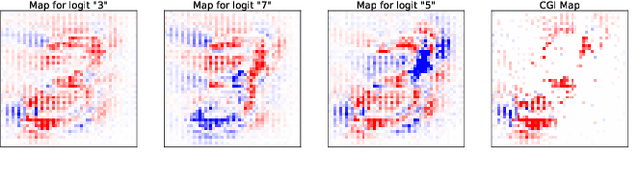
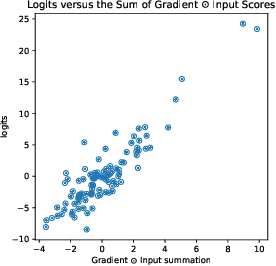
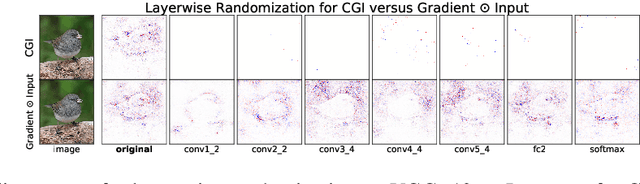
There is great interest in "saliency methods" (also called "attribution methods"), which give "explanations" for a deep net's decision, by assigning a "score" to each feature/pixel in the input. Their design usually involves credit-assignment via the gradient of the output with respect to input. Recently Adebayo et al. [arXiv:1810.03292] questioned the validity of many of these methods since they do not pass simple *sanity checks* which test whether the scores shift/vanish when layers of the trained net are randomized, or when the net is retrained using random labels for inputs. We propose a simple fix to existing saliency methods that helps them pass sanity checks, which we call "competition for pixels". This involves computing saliency maps for all possible labels in the classification task, and using a simple competition among them to identify and remove less relevant pixels from the map. The simplest variant of this is "Competitive Gradient $\odot$ Input (CGI)": it is efficient, requires no additional training, and uses only the input and gradient. Some theoretical justification is provided for it (especially for ReLU networks) and its performance is empirically demonstrated.

Implicit Regularization in Deep Matrix Factorization

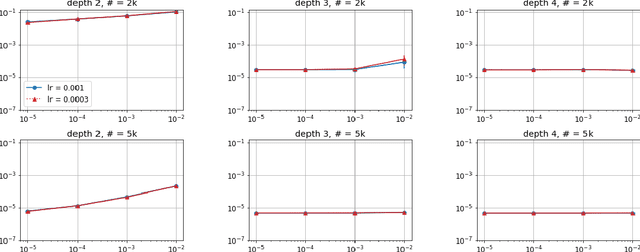
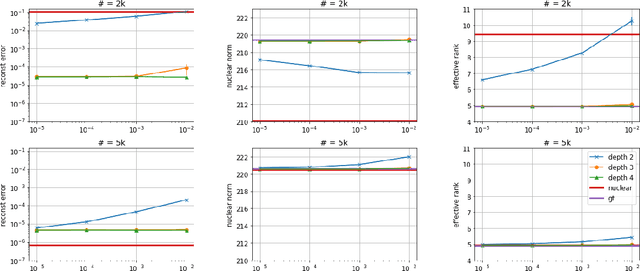
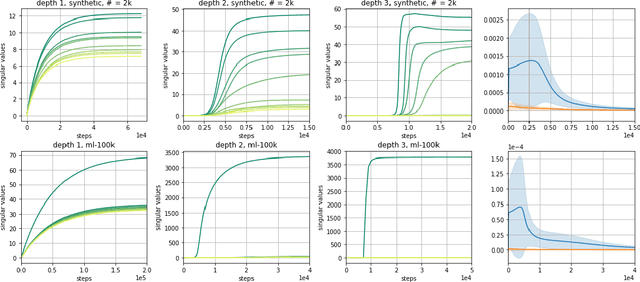
Efforts to understand the generalization mystery in deep learning have led to the belief that gradient-based optimization induces a form of implicit regularization, a bias towards models of low "complexity." We study the implicit regularization of gradient descent over deep linear neural networks for matrix completion and sensing, a model referred to as deep matrix factorization. Our first finding, supported by theory and experiments, is that adding depth to a matrix factorization enhances an implicit tendency towards low-rank solutions, oftentimes leading to more accurate recovery. Secondly, we present theoretical and empirical arguments questioning a nascent view by which implicit regularization in matrix factorization can be captured using simple mathematical norms. Our results point to the possibility that the language of standard regularizers may not be rich enough to fully encompass the implicit regularization brought forth by gradient-based optimization.

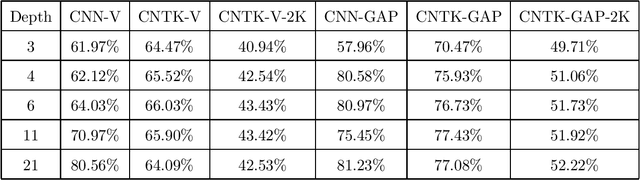
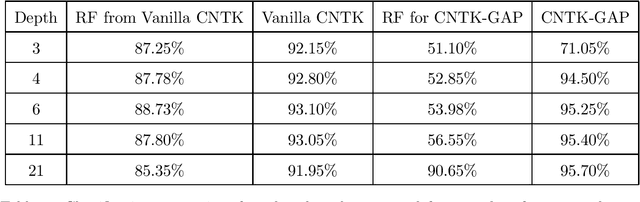
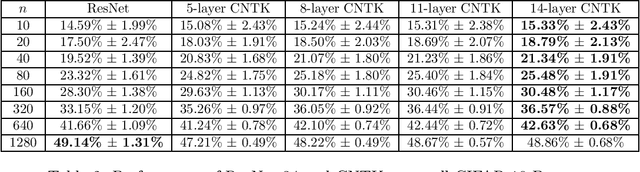
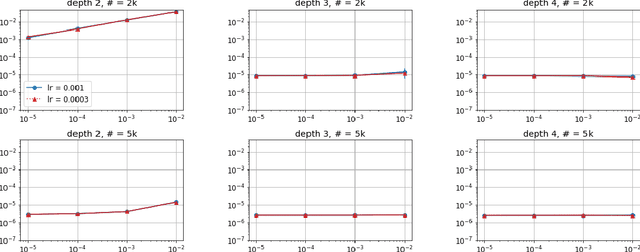
On Exact Computation with an Infinitely Wide Neural Net

How well does a classic deep net architecture like AlexNet or VGG19 classify on a standard dataset such as CIFAR-10 when its "width" --- namely, number of channels in convolutional layers, and number of nodes in fully-connected internal layers --- is allowed to increase to infinity? Such questions have come to the forefront in the quest to theoretically understand deep learning and its mysteries about optimization and generalization. They also connect deep learning to notions such as Gaussian processes and kernels. A recent paper [Jacot et al., 2018] introduced the Neural Tangent Kernel (NTK) which captures the behavior of fully-connected deep nets in the infinite width limit trained by gradient descent; this object was implicit in some other recent papers. A subsequent paper [Lee et al., 2019] gave heuristic Monte Carlo methods to estimate the NTK and its extension, Convolutional Neural Tangent Kernel (CNTK) and used this to try to understand the limiting behavior on datasets like CIFAR-10. The current paper gives the first efficient exact algorithm (based upon dynamic programming) for computing CNTK as well as an efficient GPU implementation of this algorithm. This results in a significant new benchmark for performance of a pure kernel-based method on CIFAR-10, being 10% higher than the methods reported in [Novak et al., 2019], and only 5% lower than the performance of the corresponding finite deep net architecture (once batch normalization etc. are turned off). We give the first non-asymptotic proof showing that a fully-trained sufficiently wide net is indeed equivalent to the kernel regression predictor using NTK. Our experiments also demonstrate that earlier Monte Carlo approximation can degrade the performance significantly, thus highlighting the power of our exact kernel computation, which we have applied even to the full CIFAR-10 dataset and 20-layer nets.

A Theoretical Analysis of Contrastive Unsupervised Representation Learning

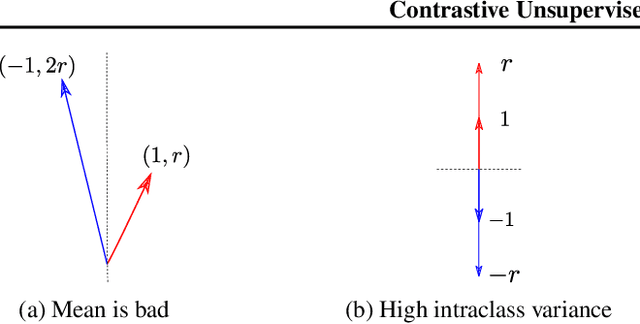
Recent empirical works have successfully used unlabeled data to learn feature representations that are broadly useful in downstream classification tasks. Several of these methods are reminiscent of the well-known word2vec embedding algorithm: leveraging availability of pairs of semantically "similar" data points and "negative samples," the learner forces the inner product of representations of similar pairs with each other to be higher on average than with negative samples. The current paper uses the term contrastive learning for such algorithms and presents a theoretical framework for analyzing them by introducing latent classes and hypothesizing that semantically similar points are sampled from the same latent class. This framework allows us to show provable guarantees on the performance of the learned representations on the average classification task that is comprised of a subset of the same set of latent classes. Our generalization bound also shows that learned representations can reduce (labeled) sample complexity on downstream tasks. We conduct controlled experiments in both the text and image domains to support the theory.

Fine-Grained Analysis of Optimization and Generalization for Overparameterized Two-Layer Neural Networks

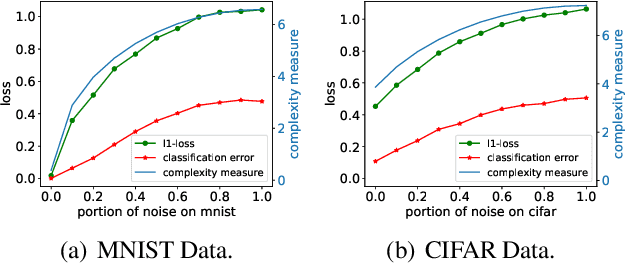
Recent works have cast some light on the mystery of why deep nets fit any data and generalize despite being very overparametrized. This paper analyzes training and generalization for a simple 2-layer ReLU net with random initialization, and provides the following improvements over recent works: (i) Using a tighter characterization of training speed than recent papers, an explanation for why training a neural net with random labels leads to slower training, as originally observed in [Zhang et al. ICLR'17]. (ii) Generalization bound independent of network size, using a data-dependent complexity measure. Our measure distinguishes clearly between random labels and true labels on MNIST and CIFAR, as shown by experiments. Moreover, recent papers require sample complexity to increase (slowly) with the size, while our sample complexity is completely independent of the network size. (iii) Learnability of a broad class of smooth functions by 2-layer ReLU nets trained via gradient descent. The key idea is to track dynamics of training and generalization via properties of a related kernel.

Theoretical Analysis of Auto Rate-Tuning by Batch Normalization

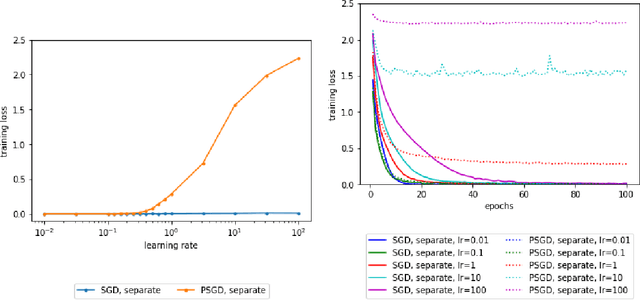
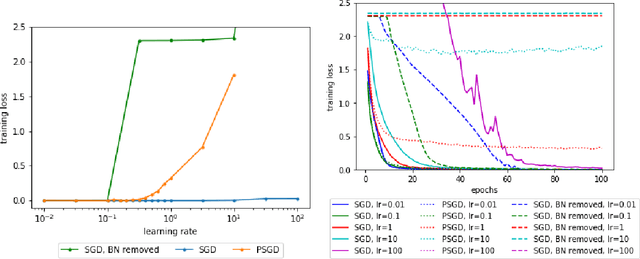
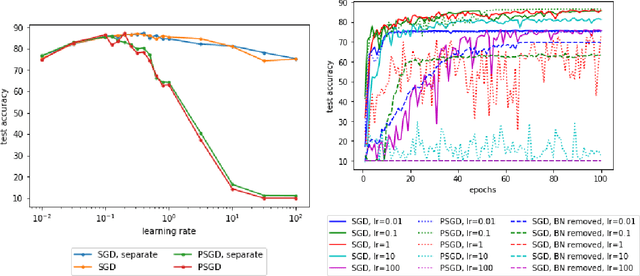
Batch Normalization (BN) has become a cornerstone of deep learning across diverse architectures, appearing to help optimization as well as generalization. While the idea makes intuitive sense, theoretical analysis of its effectiveness has been lacking. Here theoretical support is provided for one of its conjectured properties, namely, the ability to allow gradient descent to succeed with less tuning of learning rates. It is shown that even if we fix the learning rate of scale-invariant parameters (e.g., weights of each layer with BN) to a constant (say, $0.3$), gradient descent still approaches a stationary point (i.e., a solution where gradient is zero) in the rate of $T^{-1/2}$ in $T$ iterations, asymptotically matching the best bound for gradient descent with well-tuned learning rates. A similar result with convergence rate $T^{-1/4}$ is also shown for stochastic gradient descent.

Stronger generalization bounds for deep nets via a compression approach

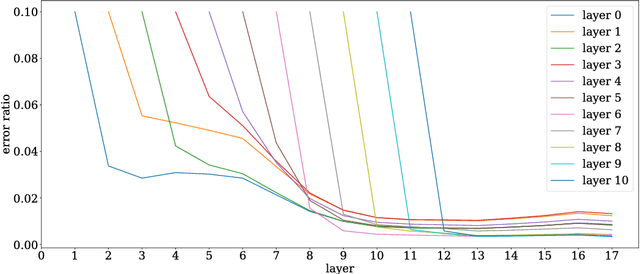
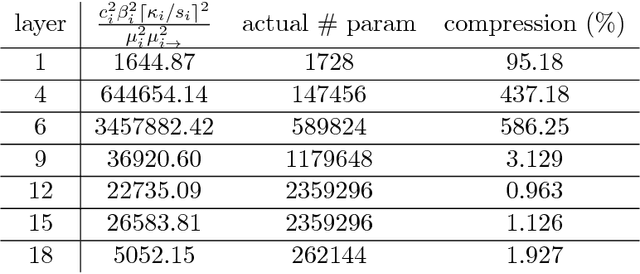
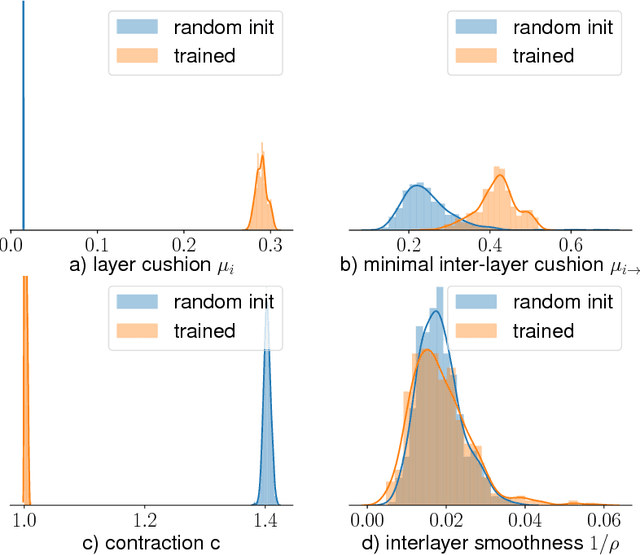
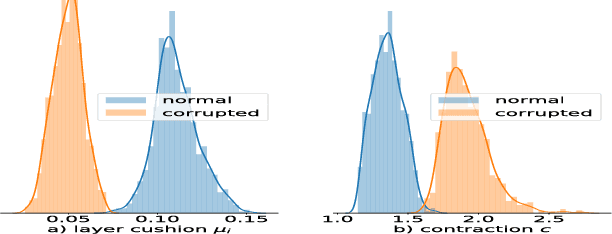
Deep nets generalize well despite having more parameters than the number of training samples. Recent works try to give an explanation using PAC-Bayes and Margin-based analyses, but do not as yet result in sample complexity bounds better than naive parameter counting. The current paper shows generalization bounds that're orders of magnitude better in practice. These rely upon new succinct reparametrizations of the trained net --- a compression that is explicit and efficient. These yield generalization bounds via a simple compression-based framework introduced here. Our results also provide some theoretical justification for widespread empirical success in compressing deep nets. Analysis of correctness of our compression relies upon some newly identified \textquotedblleft noise stability\textquotedblright properties of trained deep nets, which are also experimentally verified. The study of these properties and resulting generalization bounds are also extended to convolutional nets, which had eluded earlier attempts on proving generalization.

Linear Algebraic Structure of Word Senses, with Applications to Polysemy

Word embeddings are ubiquitous in NLP and information retrieval, but it is unclear what they represent when the word is polysemous. Here it is shown that multiple word senses reside in linear superposition within the word embedding and simple sparse coding can recover vectors that approximately capture the senses. The success of our approach, which applies to several embedding methods, is mathematically explained using a variant of the random walk on discourses model (Arora et al., 2016). A novel aspect of our technique is that each extracted word sense is accompanied by one of about 2000 "discourse atoms" that gives a succinct description of which other words co-occur with that word sense. Discourse atoms can be of independent interest, and make the method potentially more useful. Empirical tests are used to verify and support the theory.