Understanding Gradient Descent on Edge of Stability in Deep Learning

Deep learning experiments in Cohen et al. (2021) using deterministic Gradient Descent (GD) revealed an {\em Edge of Stability (EoS)} phase when learning rate (LR) and sharpness (\emph{i.e.}, the largest eigenvalue of Hessian) no longer behave as in traditional optimization. Sharpness stabilizes around $2/$LR and loss goes up and down across iterations, yet still with an overall downward trend. The current paper mathematically analyzes a new mechanism of implicit regularization in the EoS phase, whereby GD updates due to non-smooth loss landscape turn out to evolve along some deterministic flow on the manifold of minimum loss. This is in contrast to many previous results about implicit bias either relying on infinitesimal updates or noise in gradient. Formally, for any smooth function $L$ with certain regularity condition, this effect is demonstrated for (1) {\em Normalized GD}, i.e., GD with a varying LR $ \eta_t =\frac{ \eta }{ || \nabla L(x(t)) || } $ and loss $L$; (2) GD with constant LR and loss $\sqrt{L}$. Both provably enter the Edge of Stability, with the associated flow on the manifold minimizing $\lambda_{\max}(\nabla^2 L)$. The above theoretical results have been corroborated by an experimental study.

Adaptive Gradient Methods with Local Guarantees

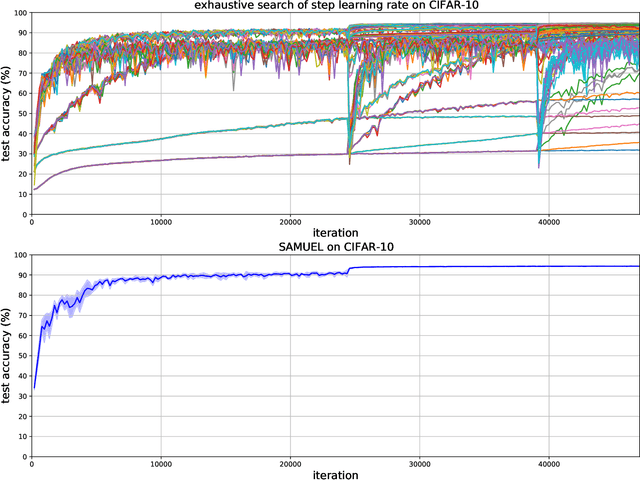
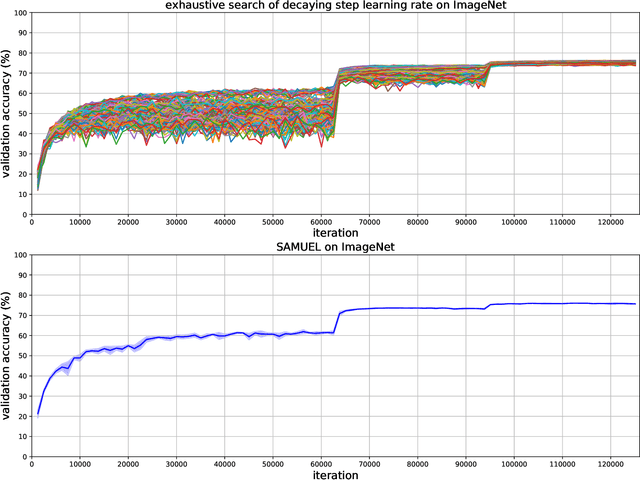
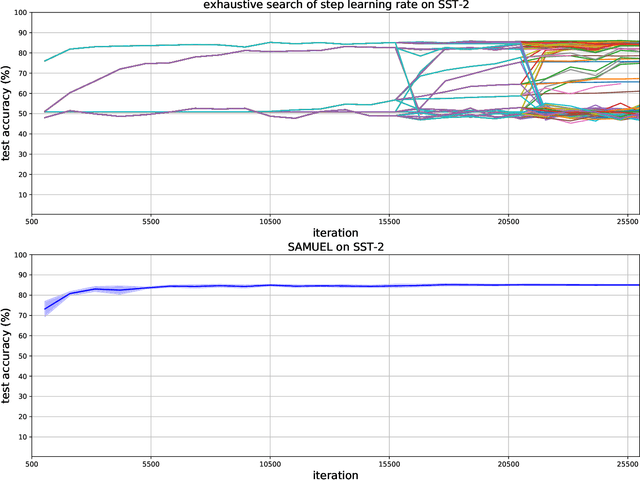
Adaptive gradient methods are the method of choice for optimization in machine learning and used to train the largest deep models. In this paper we study the problem of learning a local preconditioner, that can change as the data is changing along the optimization trajectory. We propose an adaptive gradient method that has provable adaptive regret guarantees vs. the best local preconditioner. To derive this guarantee, we prove a new adaptive regret bound in online learning that improves upon previous adaptive online learning methods. We demonstrate the robustness of our method in automatically choosing the optimal learning rate schedule for popular benchmarking tasks in vision and language domains. Without the need to manually tune a learning rate schedule, our method can, in a single run, achieve comparable and stable task accuracy as a fine-tuned optimizer.

Understanding Contrastive Learning Requires Incorporating Inductive Biases

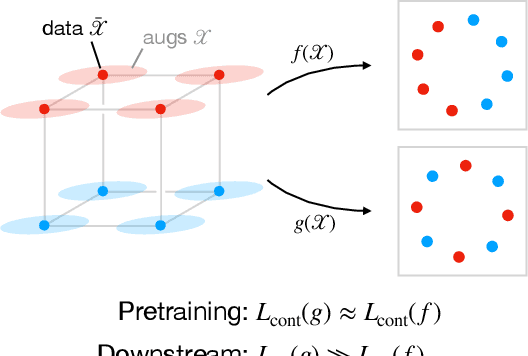
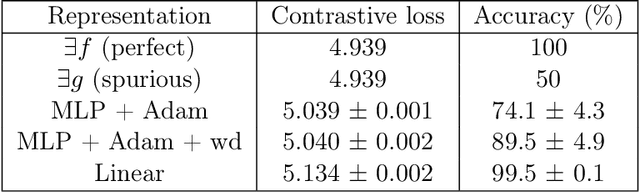
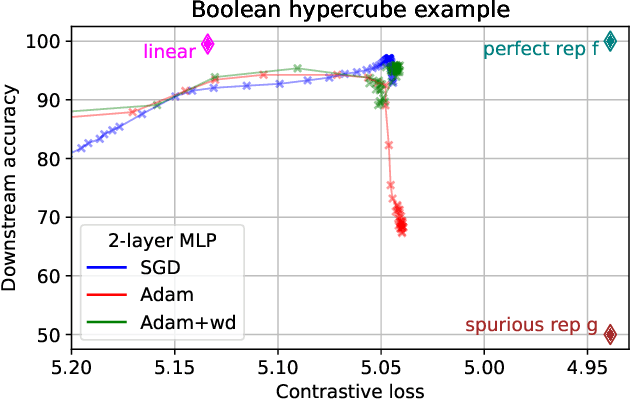
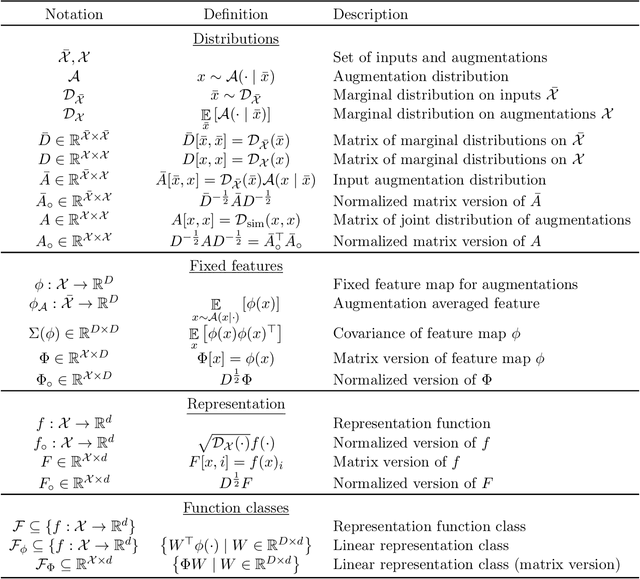
Contrastive learning is a popular form of self-supervised learning that encourages augmentations (views) of the same input to have more similar representations compared to augmentations of different inputs. Recent attempts to theoretically explain the success of contrastive learning on downstream classification tasks prove guarantees depending on properties of {\em augmentations} and the value of {\em contrastive loss} of representations. We demonstrate that such analyses, that ignore {\em inductive biases} of the function class and training algorithm, cannot adequately explain the success of contrastive learning, even {\em provably} leading to vacuous guarantees in some settings. Extensive experiments on image and text domains highlight the ubiquity of this problem -- different function classes and algorithms behave very differently on downstream tasks, despite having the same augmentations and contrastive losses. Theoretical analysis is presented for the class of linear representations, where incorporating inductive biases of the function class allows contrastive learning to work with less stringent conditions compared to prior analyses.

Evaluating Gradient Inversion Attacks and Defenses in Federated Learning

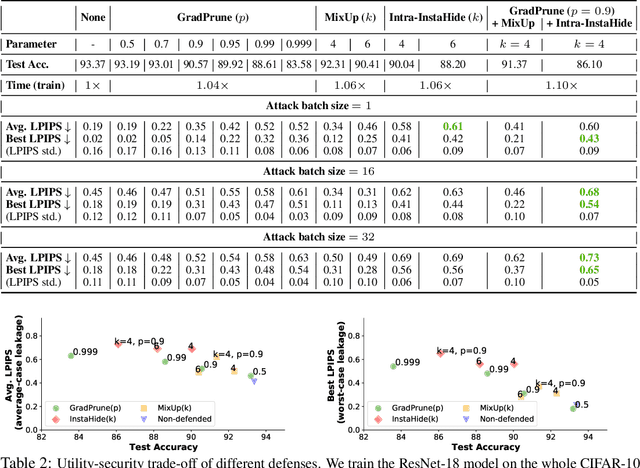
Gradient inversion attack (or input recovery from gradient) is an emerging threat to the security and privacy preservation of Federated learning, whereby malicious eavesdroppers or participants in the protocol can recover (partially) the clients' private data. This paper evaluates existing attacks and defenses. We find that some attacks make strong assumptions about the setup. Relaxing such assumptions can substantially weaken these attacks. We then evaluate the benefits of three proposed defense mechanisms against gradient inversion attacks. We show the trade-offs of privacy leakage and data utility of these defense methods, and find that combining them in an appropriate manner makes the attack less effective, even under the original strong assumptions. We also estimate the computation cost of end-to-end recovery of a single image under each evaluated defense. Our findings suggest that the state-of-the-art attacks can currently be defended against with minor data utility loss, as summarized in a list of potential strategies. Our code is available at: https://github.com/Princeton-SysML/GradAttack.

On Predicting Generalization using GANs

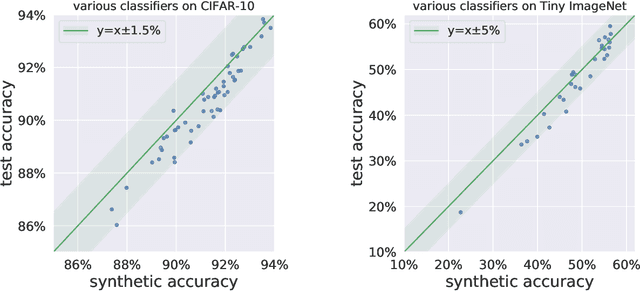
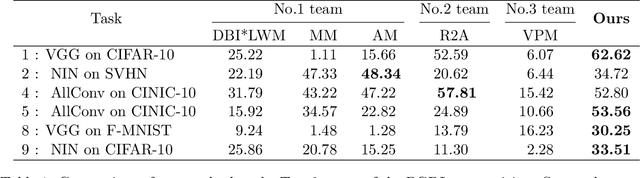
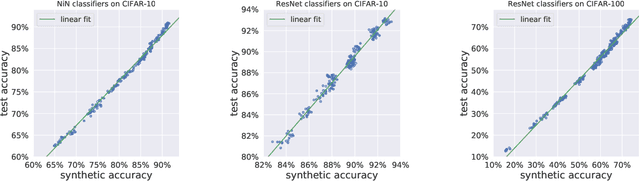
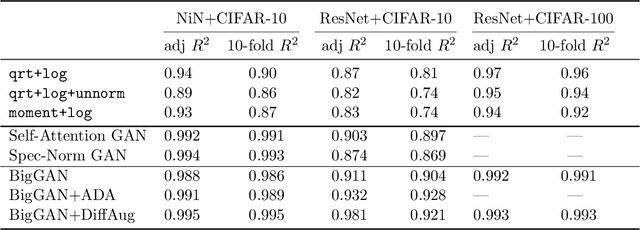
Research on generalization bounds for deep networks seeks to give ways to predict test error using just the training dataset and the network parameters. While generalization bounds can give many insights about architecture design, training algorithms etc., what they do not currently do is yield good predictions for actual test error. A recently introduced Predicting Generalization in Deep Learning competition aims to encourage discovery of methods to better predict test error. The current paper investigates a simple idea: can test error be predicted using 'synthetic data' produced using a Generative Adversarial Network (GAN) that was trained on the same training dataset? Upon investigating several GAN models and architectures, we find that this turns out to be the case. In fact, using GANs pre-trained on standard datasets, the test error can be predicted without requiring any additional hyper-parameter tuning. This result is surprising because GANs have well-known limitations (e.g. mode collapse) and are known to not learn the data distribution accurately. Yet the generated samples are good enough to substitute for test data. Several additional experiments are presented to explore reasons why GANs do well at this task. In addition to a new approach for predicting generalization, the counter-intuitive phenomena presented in our work may also call for a better understanding of GANs' strengths and limitations.

Gradient Descent on Two-layer Nets: Margin Maximization and Simplicity Bias

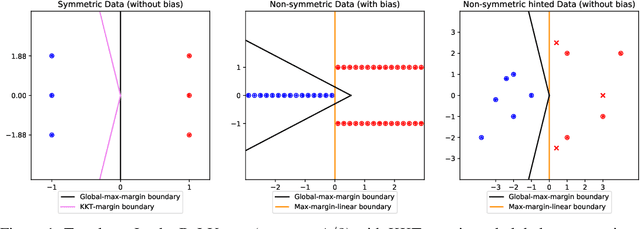
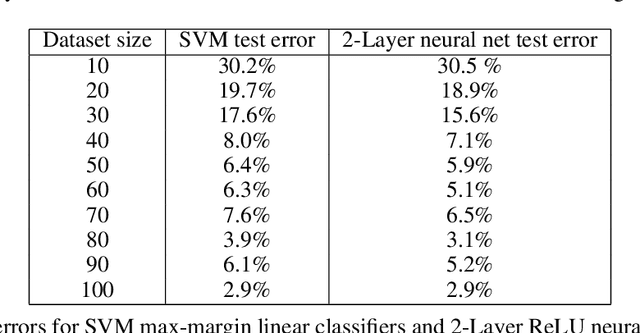
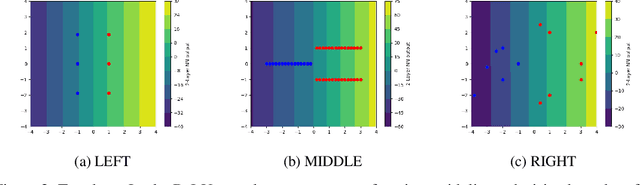
The generalization mystery of overparametrized deep nets has motivated efforts to understand how gradient descent (GD) converges to low-loss solutions that generalize well. Real-life neural networks are initialized from small random values and trained with cross-entropy loss for classification (unlike the "lazy" or "NTK" regime of training where analysis was more successful), and a recent sequence of results (Lyu and Li, 2020; Chizat and Bach, 2020; Ji and Telgarsky, 2020) provide theoretical evidence that GD may converge to the "max-margin" solution with zero loss, which presumably generalizes well. However, the global optimality of margin is proved only in some settings where neural nets are infinitely or exponentially wide. The current paper is able to establish this global optimality for two-layer Leaky ReLU nets trained with gradient flow on linearly separable and symmetric data, regardless of the width. The analysis also gives some theoretical justification for recent empirical findings (Kalimeris et al., 2019) on the so-called simplicity bias of GD towards linear or other "simple" classes of solutions, especially early in training. On the pessimistic side, the paper suggests that such results are fragile. A simple data manipulation can make gradient flow converge to a linear classifier with suboptimal margin.

What Happens after SGD Reaches Zero Loss? --A Mathematical Framework

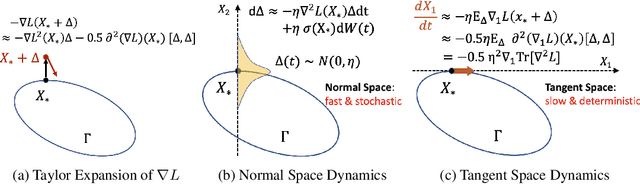
Understanding the implicit bias of Stochastic Gradient Descent (SGD) is one of the key challenges in deep learning, especially for overparametrized models, where the local minimizers of the loss function $L$ can form a manifold. Intuitively, with a sufficiently small learning rate $\eta$, SGD tracks Gradient Descent (GD) until it gets close to such manifold, where the gradient noise prevents further convergence. In such a regime, Blanc et al. (2020) proved that SGD with label noise locally decreases a regularizer-like term, the sharpness of loss, $\mathrm{tr}[\nabla^2 L]$. The current paper gives a general framework for such analysis by adapting ideas from Katzenberger (1991). It allows in principle a complete characterization for the regularization effect of SGD around such manifold -- i.e., the "implicit bias" -- using a stochastic differential equation (SDE) describing the limiting dynamics of the parameters, which is determined jointly by the loss function and the noise covariance. This yields some new results: (1) a global analysis of the implicit bias valid for $\eta^{-2}$ steps, in contrast to the local analysis of Blanc et al. (2020) that is only valid for $\eta^{-1.6}$ steps and (2) allowing arbitrary noise covariance. As an application, we show with arbitrary large initialization, label noise SGD can always escape the kernel regime and only requires $O(\kappa\ln d)$ samples for learning an $\kappa$-sparse overparametrized linear model in $\mathbb{R}^d$ (Woodworth et al., 2020), while GD initialized in the kernel regime requires $\Omega(d)$ samples. This upper bound is minimax optimal and improves the previous $\tilde{O}(\kappa^2)$ upper bound (HaoChen et al., 2020).

Rip van Winkle's Razor: A Simple Estimate of Overfit to Test Data

Traditional statistics forbids use of test data (a.k.a. holdout data) during training. Dwork et al. 2015 pointed out that current practices in machine learning, whereby researchers build upon each other's models, copying hyperparameters and even computer code -- amounts to implicitly training on the test set. Thus error rate on test data may not reflect the true population error. This observation initiated {\em adaptive data analysis}, which provides evaluation mechanisms with guaranteed upper bounds on this difference. With statistical query (i.e. test accuracy) feedbacks, the best upper bound is fairly pessimistic: the deviation can hit a practically vacuous value if the number of models tested is quadratic in the size of the test set. In this work, we present a simple new estimate, {\em Rip van Winkle's Razor}. It relies upon a new notion of \textquotedblleft information content\textquotedblright\ of a model: the amount of information that would have to be provided to an expert referee who is intimately familiar with the field and relevant science/math, and who has been just been woken up after falling asleep at the moment of the creation of the test data (like \textquotedblleft Rip van Winkle\textquotedblright\ of the famous fairy tale). This notion of information content is used to provide an estimate of the above deviation which is shown to be non-vacuous in many modern settings.

On the Validity of Modeling SGD with Stochastic Differential Equations

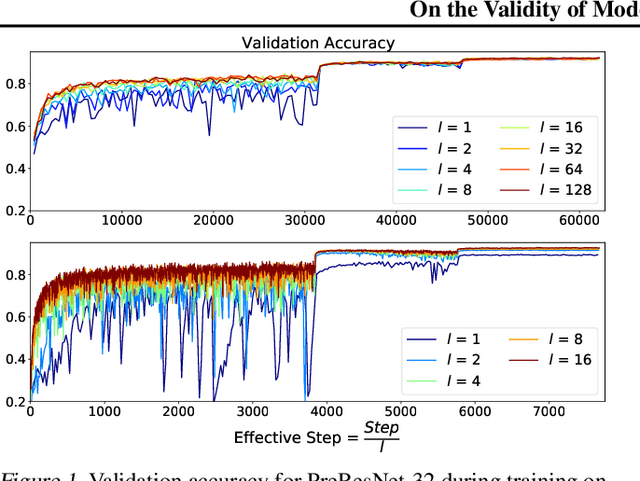
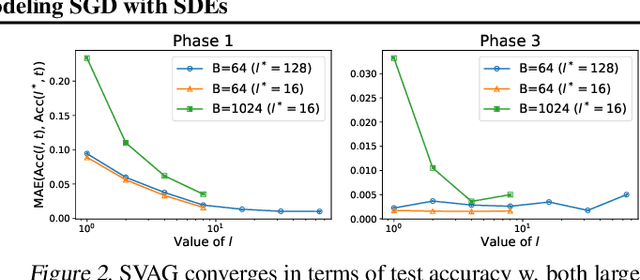
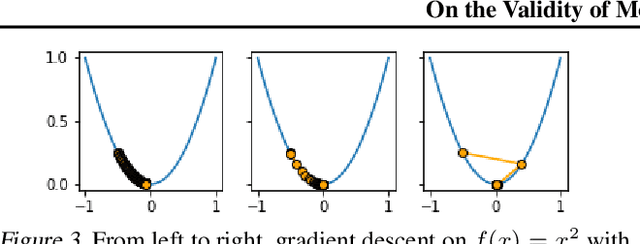
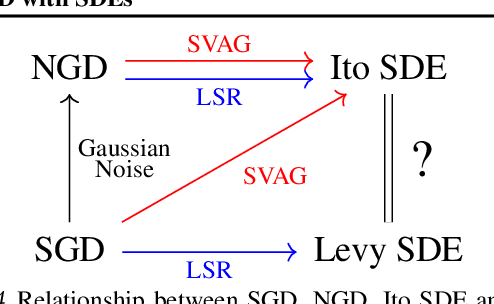
It is generally recognized that finite learning rate (LR), in contrast to infinitesimal LR, is important for good generalization in real-life deep nets. Most attempted explanations propose approximating finite-LR SGD with Ito Stochastic Differential Equations (SDEs). But formal justification for this approximation (e.g., (Li et al., 2019a)) only applies to SGD with tiny LR. Experimental verification of the approximation appears computationally infeasible. The current paper clarifies the picture with the following contributions: (a) An efficient simulation algorithm SVAG that provably converges to the conventionally used Ito SDE approximation. (b) Experiments using this simulation to demonstrate that the previously proposed SDE approximation can meaningfully capture the training and generalization properties of common deep nets. (c) A provable and empirically testable necessary condition for the SDE approximation to hold and also its most famous implication, the linear scaling rule (Smith et al., 2020; Goyal et al., 2017). The analysis also gives rigorous insight into why the SDE approximation may fail.

Why Are Convolutional Nets More Sample-Efficient than Fully-Connected Nets?

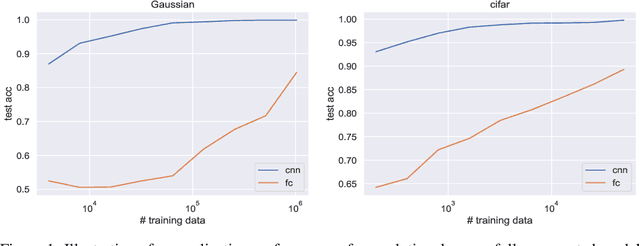
Convolutional neural networks often dominate fully-connected counterparts in generalization performance, especially on image classification tasks. This is often explained in terms of 'better inductive bias'. However, this has not been made mathematically rigorous, and the hurdle is that the fully connected net can always simulate the convolutional net (for a fixed task). Thus the training algorithm plays a role. The current work describes a natural task on which a provable sample complexity gap can be shown, for standard training algorithms. We construct a single natural distribution on $\mathbb{R}^d\times\{\pm 1\}$ on which any orthogonal-invariant algorithm (i.e. fully-connected networks trained with most gradient-based methods from gaussian initialization) requires $\Omega(d^2)$ samples to generalize while $O(1)$ samples suffice for convolutional architectures. Furthermore, we demonstrate a single target function, learning which on all possible distributions leads to an $O(1)$ vs $\Omega(d^2/\varepsilon)$ gap. The proof relies on the fact that SGD on fully-connected network is orthogonal equivariant. Similar results are achieved for $\ell_2$ regression and adaptive training algorithms, e.g. Adam and AdaGrad, which are only permutation equivariant.