Samuel Yen-Chi Chen
Quantum Super-resolution by Adaptive Non-local Observables
Jan 20, 2026Abstract:Super-resolution (SR) seeks to reconstruct high-resolution (HR) data from low-resolution (LR) observations. Classical deep learning methods have advanced SR substantially, but require increasingly deeper networks, large datasets, and heavy computation to capture fine-grained correlations. In this work, we present the \emph{first study} to investigate quantum circuits for SR. We propose a framework based on Variational Quantum Circuits (VQCs) with \emph{Adaptive Non-Local Observable} (ANO) measurements. Unlike conventional VQCs with fixed Pauli readouts, ANO introduces trainable multi-qubit Hermitian observables, allowing the measurement process to adapt during training. This design leverages the high-dimensional Hilbert space of quantum systems and the representational structure provided by entanglement and superposition. Experiments demonstrate that ANO-VQCs achieve up to five-fold higher resolution with a relatively small model size, suggesting a promising new direction at the intersection of quantum machine learning and super-resolution.
TITAN: A Trajectory-Informed Technique for Adaptive Parameter Freezing in Large-Scale VQE
Sep 18, 2025



Abstract:Variational quantum Eigensolver (VQE) is a leading candidate for harnessing quantum computers to advance quantum chemistry and materials simulations, yet its training efficiency deteriorates rapidly for large Hamiltonians. Two issues underlie this bottleneck: (i) the no-cloning theorem imposes a linear growth in circuit evaluations with the number of parameters per gradient step; and (ii) deeper circuits encounter barren plateaus (BPs), leading to exponentially increasing measurement overheads. To address these challenges, here we propose a deep learning framework, dubbed Titan, which identifies and freezes inactive parameters of a given ansatze at initialization for a specific class of Hamiltonians, reducing the optimization overhead without sacrificing accuracy. The motivation of Titan starts with our empirical findings that a subset of parameters consistently has a negligible influence on training dynamics. Its design combines a theoretically grounded data construction strategy, ensuring each training example is informative and BP-resilient, with an adaptive neural architecture that generalizes across ansatze of varying sizes. Across benchmark transverse-field Ising models, Heisenberg models, and multiple molecule systems up to 30 qubits, Titan achieves up to 3 times faster convergence and 40% to 60% fewer circuit evaluations than state-of-the-art baselines, while matching or surpassing their estimation accuracy. By proactively trimming parameter space, Titan lowers hardware demands and offers a scalable path toward utilizing VQE to advance practical quantum chemistry and materials science.
Quantum Machine Learning, Quantitative Trading, Reinforcement Learning, Deep Learning
Sep 11, 2025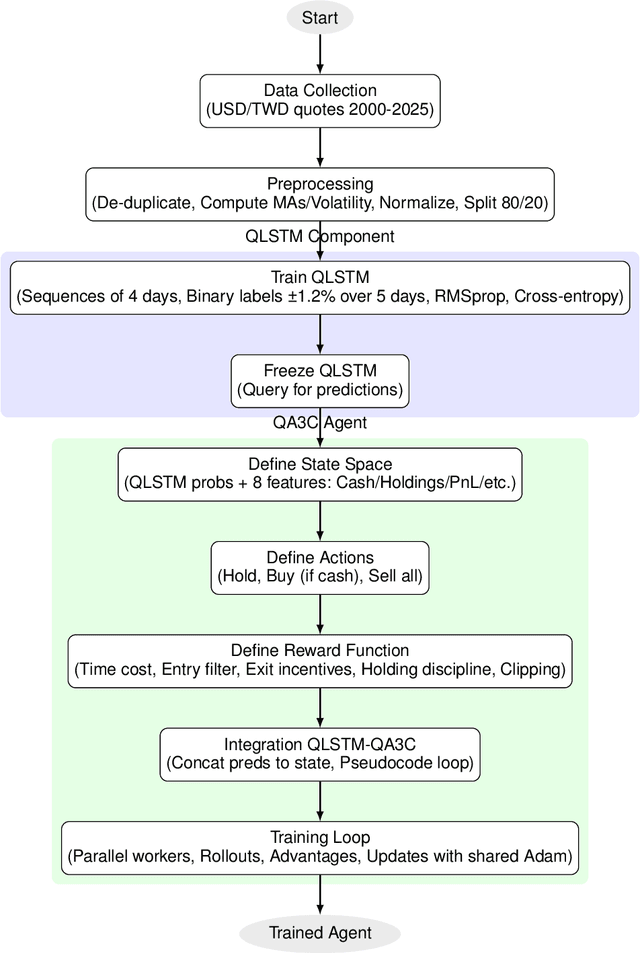
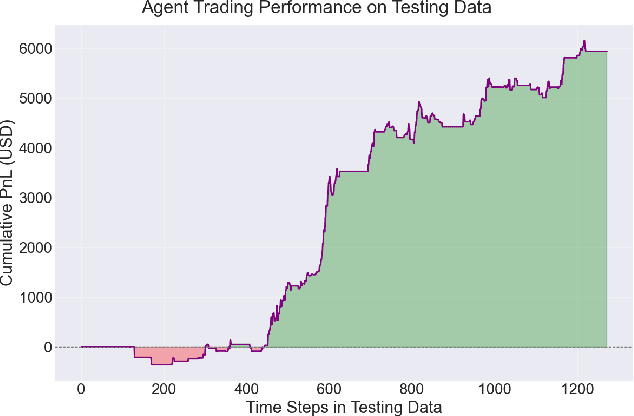
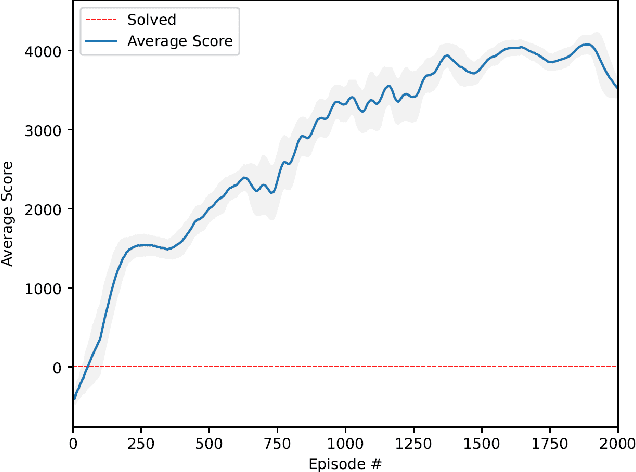

Abstract:The convergence of quantum-inspired neural networks and deep reinforcement learning offers a promising avenue for financial trading. We implemented a trading agent for USD/TWD by integrating Quantum Long Short-Term Memory (QLSTM) for short-term trend prediction with Quantum Asynchronous Advantage Actor-Critic (QA3C), a quantum-enhanced variant of the classical A3C. Trained on data from 2000-01-01 to 2025-04-30 (80\% training, 20\% testing), the long-only agent achieves 11.87\% return over around 5 years with 0.92\% max drawdown, outperforming several currency ETFs. We detail state design (QLSTM features and indicators), reward function for trend-following/risk control, and multi-core training. Results show hybrid models yield competitive FX trading performance. Implications include QLSTM's effectiveness for small-profit trades with tight risk and future enhancements. Key hyperparameters: QLSTM sequence length$=$4, QA3C workers$=$8. Limitations: classical quantum simulation and simplified strategy. \footnote{The views expressed in this article are those of the authors and do not represent the views of Wells Fargo. This article is for informational purposes only. Nothing contained in this article should be construed as investment advice. Wells Fargo makes no express or implied warranties and expressly disclaims all legal, tax, and accounting implications related to this article.
Quantum Long Short-term Memory with Differentiable Architecture Search
Aug 20, 2025



Abstract:Recent advances in quantum computing and machine learning have given rise to quantum machine learning (QML), with growing interest in learning from sequential data. Quantum recurrent models like QLSTM are promising for time-series prediction, NLP, and reinforcement learning. However, designing effective variational quantum circuits (VQCs) remains challenging and often task-specific. To address this, we propose DiffQAS-QLSTM, an end-to-end differentiable framework that optimizes both VQC parameters and architecture selection during training. Our results show that DiffQAS-QLSTM consistently outperforms handcrafted baselines, achieving lower loss across diverse test settings. This approach opens the door to scalable and adaptive quantum sequence learning.
Q-DPTS: Quantum Differentially Private Time Series Forecasting via Variational Quantum Circuits
Aug 07, 2025Abstract:Time series forecasting is vital in domains where data sensitivity is paramount, such as finance and energy systems. While Differential Privacy (DP) provides theoretical guarantees to protect individual data contributions, its integration especially via DP-SGD often impairs model performance due to injected noise. In this paper, we propose Q-DPTS, a hybrid quantum-classical framework for Quantum Differentially Private Time Series Forecasting. Q-DPTS combines Variational Quantum Circuits (VQCs) with per-sample gradient clipping and Gaussian noise injection, ensuring rigorous $(\epsilon, \delta)$-differential privacy. The expressiveness of quantum models enables improved robustness against the utility loss induced by DP mechanisms. We evaluate Q-DPTS on the ETT (Electricity Transformer Temperature) dataset, a standard benchmark for long-term time series forecasting. Our approach is compared against both classical and quantum baselines, including LSTM, QASA, QRWKV, and QLSTM. Results demonstrate that Q-DPTS consistently achieves lower prediction error under the same privacy budget, indicating a favorable privacy-utility trade-off. This work presents one of the first explorations into quantum-enhanced differentially private forecasting, offering promising directions for secure and accurate time series modeling in privacy-critical scenarios.
Benchmarking Quantum and Classical Sequential Models for Urban Telecommunication Forecasting
Aug 06, 2025Abstract:In this study, we evaluate the performance of classical and quantum-inspired sequential models in forecasting univariate time series of incoming SMS activity (SMS-in) using the Milan Telecommunication Activity Dataset. Due to data completeness limitations, we focus exclusively on the SMS-in signal for each spatial grid cell. We compare five models, LSTM (baseline), Quantum LSTM (QLSTM), Quantum Adaptive Self-Attention (QASA), Quantum Receptance Weighted Key-Value (QRWKV), and Quantum Fast Weight Programmers (QFWP), under varying input sequence lengths (4, 8, 12, 16, 32 and 64). All models are trained to predict the next 10-minute SMS-in value based solely on historical values within a given sequence window. Our findings indicate that different models exhibit varying sensitivities to sequence length, suggesting that quantum enhancements are not universally advantageous. Rather, the effectiveness of quantum modules is highly dependent on the specific task and architectural design, reflecting inherent trade-offs among model size, parameterization strategies, and temporal modeling capabilities.
Quantum Feature Optimization for Enhanced Clustering of Blockchain Transaction Data
May 22, 2025Abstract:Blockchain transaction data exhibits high dimensionality, noise, and intricate feature entanglement, presenting significant challenges for traditional clustering algorithms. In this study, we conduct a comparative analysis of three clustering approaches: (1) Classical K-Means Clustering, applied to pre-processed feature representations; (2) Hybrid Clustering, wherein classical features are enhanced with quantum random features extracted using randomly initialized quantum neural networks (QNNs); and (3) Fully Quantum Clustering, where a QNN is trained in a self-supervised manner leveraging a SwAV-based loss function to optimize the feature space for clustering directly. The proposed experimental framework systematically investigates the impact of quantum circuit depth and the number of learned prototypes, demonstrating that even shallow quantum circuits can effectively extract meaningful non-linear representations, significantly improving clustering performance.
Quantum-Enhanced Parameter-Efficient Learning for Typhoon Trajectory Forecasting
May 14, 2025



Abstract:Typhoon trajectory forecasting is essential for disaster preparedness but remains computationally demanding due to the complexity of atmospheric dynamics and the resource requirements of deep learning models. Quantum-Train (QT), a hybrid quantum-classical framework that leverages quantum neural networks (QNNs) to generate trainable parameters exclusively during training, eliminating the need for quantum hardware at inference time. Building on QT's success across multiple domains, including image classification, reinforcement learning, flood prediction, and large language model (LLM) fine-tuning, we introduce Quantum Parameter Adaptation (QPA) for efficient typhoon forecasting model learning. Integrated with an Attention-based Multi-ConvGRU model, QPA enables parameter-efficient training while maintaining predictive accuracy. This work represents the first application of quantum machine learning (QML) to large-scale typhoon trajectory prediction, offering a scalable and energy-efficient approach to climate modeling. Our results demonstrate that QPA significantly reduces the number of trainable parameters while preserving performance, making high-performance forecasting more accessible and sustainable through hybrid quantum-classical learning.
Addressing the Current Challenges of Quantum Machine Learning through Multi-Chip Ensembles
May 13, 2025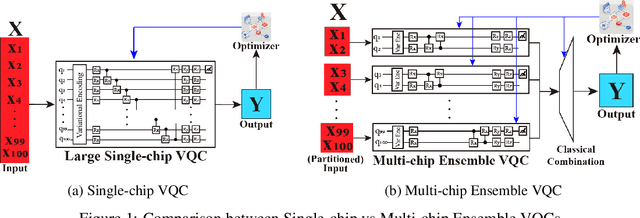

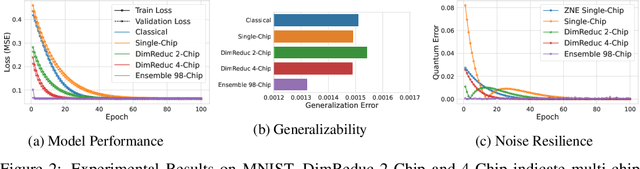

Abstract:Quantum Machine Learning (QML) holds significant promise for solving computational challenges across diverse domains. However, its practical deployment is constrained by the limitations of noisy intermediate-scale quantum (NISQ) devices, including noise, limited scalability, and trainability issues in variational quantum circuits (VQCs). We introduce the multi-chip ensemble VQC framework, which partitions high-dimensional computations across smaller quantum chips to enhance scalability, trainability, and noise resilience. We show that this approach mitigates barren plateaus, reduces quantum error bias and variance, and maintains robust generalization through controlled entanglement. Designed to align with current and emerging quantum hardware, the framework demonstrates strong potential for enabling scalable QML on near-term devices, as validated by experiments on standard benchmark datasets (MNIST, FashionMNIST, CIFAR-10) and real world dataset (PhysioNet EEG).
Introduction to Quantum Machine Learning and Quantum Architecture Search
Apr 21, 2025



Abstract:Recent advancements in quantum computing (QC) and machine learning (ML) have fueled significant research efforts aimed at integrating these two transformative technologies. Quantum machine learning (QML), an emerging interdisciplinary field, leverages quantum principles to enhance the performance of ML algorithms. Concurrently, the exploration of systematic and automated approaches for designing high-performance quantum circuit architectures for QML tasks has gained prominence, as these methods empower researchers outside the quantum computing domain to effectively utilize quantum-enhanced tools. This tutorial will provide an in-depth overview of recent breakthroughs in both areas, highlighting their potential to expand the application landscape of QML across diverse fields.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge