Identification and Adaptive Control of Markov Jump Systems: Sample Complexity and Regret Bounds

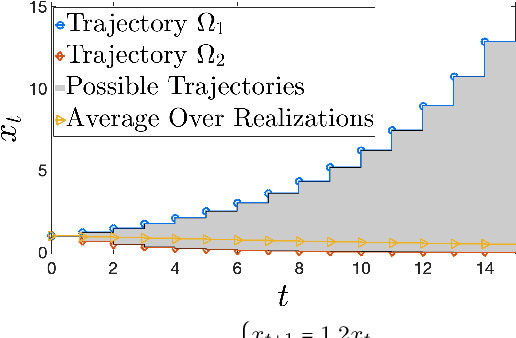
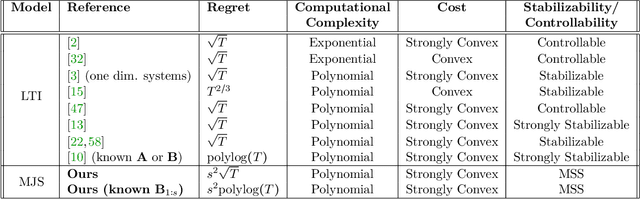
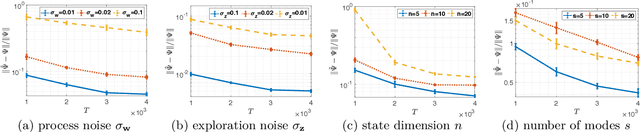
Learning how to effectively control unknown dynamical systems is crucial for intelligent autonomous systems. This task becomes a significant challenge when the underlying dynamics are changing with time. Motivated by this challenge, this paper considers the problem of controlling an unknown Markov jump linear system (MJS) to optimize a quadratic objective. By taking a model-based perspective, we consider identification-based adaptive control for MJSs. We first provide a system identification algorithm for MJS to learn the dynamics in each mode as well as the Markov transition matrix, underlying the evolution of the mode switches, from a single trajectory of the system states, inputs, and modes. Through mixing-time arguments, sample complexity of this algorithm is shown to be $\mathcal{O}(1/\sqrt{T})$. We then propose an adaptive control scheme that performs system identification together with certainty equivalent control to adapt the controllers in an episodic fashion. Combining our sample complexity results with recent perturbation results for certainty equivalent control, we prove that when the episode lengths are appropriately chosen, the proposed adaptive control scheme achieves $\mathcal{O}(\sqrt{T})$ regret, which can be improved to $\mathcal{O}(polylog(T))$ with partial knowledge of the system. Our proof strategy introduces innovations to handle Markovian jumps and a weaker notion of stability common in MJSs. Our analysis provides insights into system theoretic quantities that affect learning accuracy and control performance. Numerical simulations are presented to further reinforce these insights.

Post-hoc Models for Performance Estimation of Machine Learning Inference

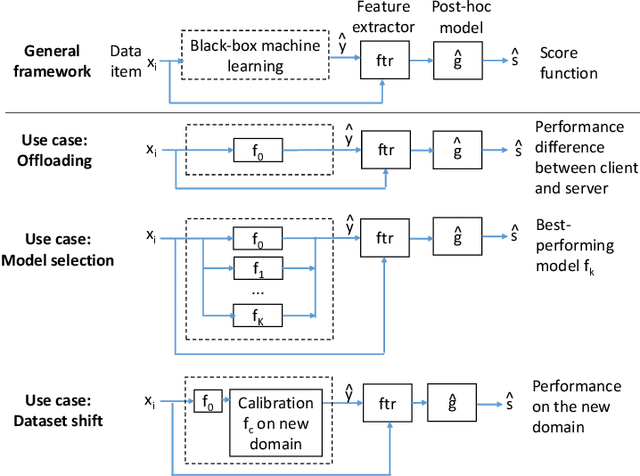
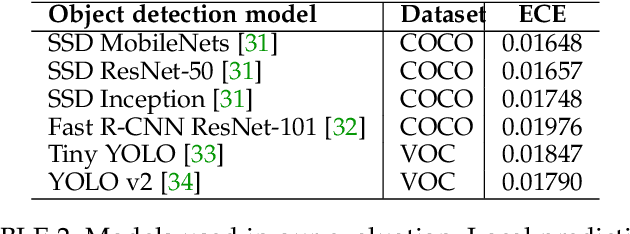
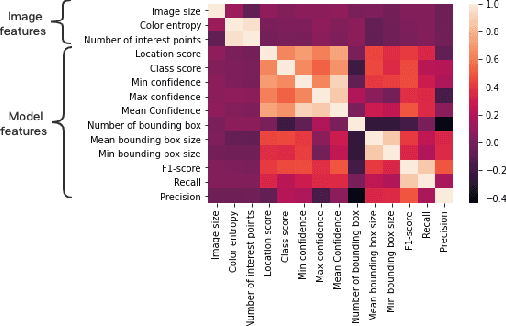
Estimating how well a machine learning model performs during inference is critical in a variety of scenarios (for example, to quantify uncertainty, or to choose from a library of available models). However, the standard accuracy estimate of softmax confidence is not versatile and cannot reliably predict different performance metrics (e.g., F1-score, recall) or the performance in different application scenarios or input domains. In this work, we systematically generalize performance estimation to a diverse set of metrics and scenarios and discuss generalized notions of uncertainty calibration. We propose the use of post-hoc models to accomplish this goal and investigate design parameters, including the model type, feature engineering, and performance metric, to achieve the best estimation quality. Emphasis is given to object detection problems and, unlike prior work, our approach enables the estimation of per-image metrics such as recall and F1-score. Through extensive experiments with computer vision models and datasets in three use cases -- mobile edge offloading, model selection, and dataset shift -- we find that proposed post-hoc models consistently outperform the standard calibrated confidence baselines. To the best of our knowledge, this is the first work to develop a unified framework to address different performance estimation problems for machine learning inference.

Certainty Equivalent Quadratic Control for Markov Jump Systems

Real-world control applications often involve complex dynamics subject to abrupt changes or variations. Markov jump linear systems (MJS) provide a rich framework for modeling such dynamics. Despite an extensive history, theoretical understanding of parameter sensitivities of MJS control is somewhat lacking. Motivated by this, we investigate robustness aspects of certainty equivalent model-based optimal control for MJS with quadratic cost function. Given the uncertainty in the system matrices and in the Markov transition matrix is bounded by $\epsilon$ and $\eta$ respectively, robustness results are established for (i) the solution to coupled Riccati equations and (ii) the optimal cost, by providing explicit perturbation bounds which decay as $\mathcal{O}(\epsilon + \eta)$ and $\mathcal{O}((\epsilon + \eta)^2)$ respectively.

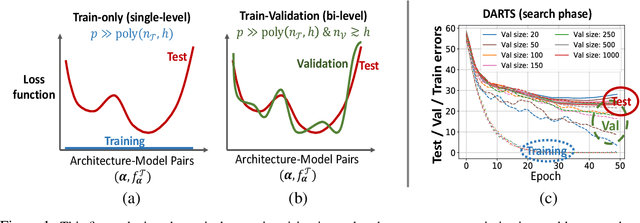
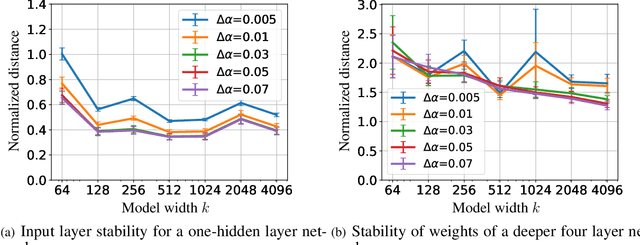
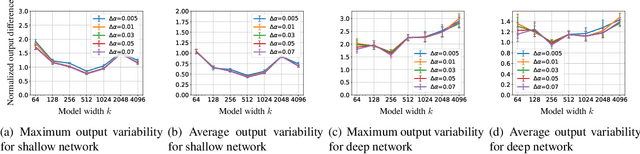
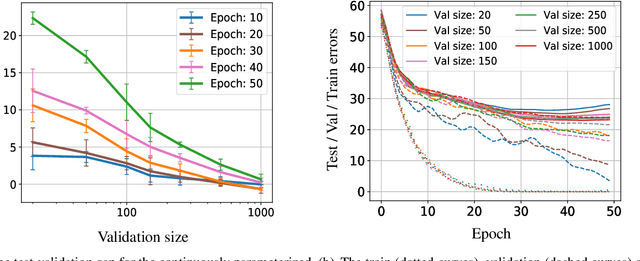
Generalization Guarantees for Neural Architecture Search with Train-Validation Split

Neural Architecture Search (NAS) is a popular method for automatically designing optimized architectures for high-performance deep learning. In this approach, it is common to use bilevel optimization where one optimizes the model weights over the training data (lower-level problem) and various hyperparameters such as the configuration of the architecture over the validation data (upper-level problem). This paper explores the statistical aspects of such problems with train-validation splits. In practice, the lower-level problem is often overparameterized and can easily achieve zero loss. Thus, a-priori it seems impossible to distinguish the right hyperparameters based on training loss alone which motivates a better understanding of the role of train-validation split. To this aim this work establishes the following results. (1) We show that refined properties of the validation loss such as risk and hyper-gradients are indicative of those of the true test loss. This reveals that the upper-level problem helps select the most generalizable model and prevent overfitting with a near-minimal validation sample size. Importantly, this is established for continuous search spaces which are highly relevant for popular differentiable search schemes. (2) We establish generalization bounds for NAS problems with an emphasis on an activation search problem. When optimized with gradient-descent, we show that the train-validation procedure returns the best (model, architecture) pair even if all architectures can perfectly fit the training data to achieve zero error. (3) Finally, we highlight rigorous connections between NAS, multiple kernel learning, and low-rank matrix learning. The latter leads to novel algorithmic insights where the solution of the upper problem can be accurately learned via efficient spectral methods to achieve near-minimal risk.

Unsupervised Multi-source Domain Adaptation Without Access to Source Data

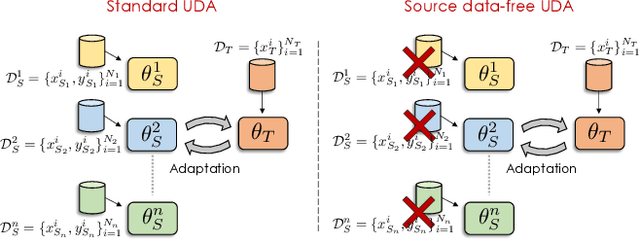
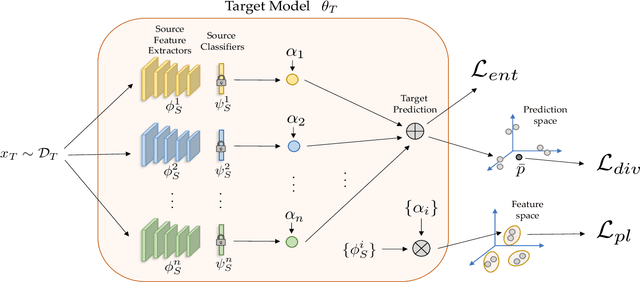
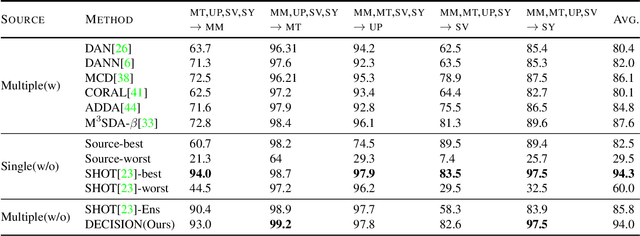
Unsupervised Domain Adaptation (UDA) aims to learn a predictor model for an unlabeled domain by transferring knowledge from a separate labeled source domain. However, most of these conventional UDA approaches make the strong assumption of having access to the source data during training, which may not be very practical due to privacy, security and storage concerns. A recent line of work addressed this problem and proposed an algorithm that transfers knowledge to the unlabeled target domain from a single source model without requiring access to the source data. However, for adaptation purposes, if there are multiple trained source models available to choose from, this method has to go through adapting each and every model individually, to check for the best source. Thus, we ask the question: can we find the optimal combination of source models, with no source data and without target labels, whose performance is no worse than the single best source? To answer this, we propose a novel and efficient algorithm which automatically combines the source models with suitable weights in such a way that it performs at least as good as the best source model. We provide intuitive theoretical insights to justify our claim. Furthermore, extensive experiments are conducted on several benchmark datasets to show the effectiveness of our algorithm, where in most cases, our method not only reaches best source accuracy but also outperforms it.

Label-Imbalanced and Group-Sensitive Classification under Overparameterization

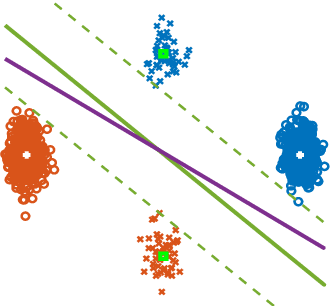
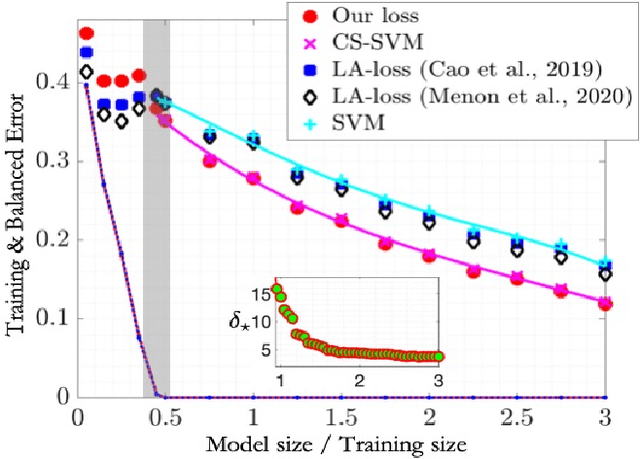
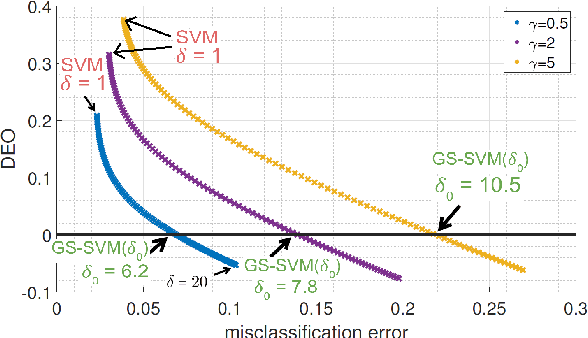
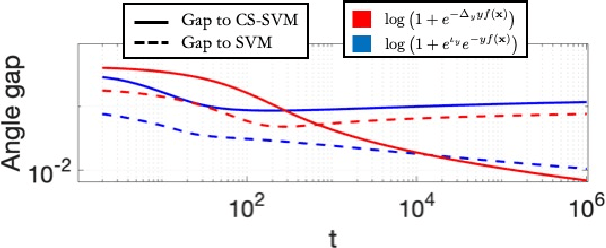
Label-imbalanced and group-sensitive classification seeks to appropriately modify standard training algorithms to optimize relevant metrics such as balanced error and/or equal opportunity. For label imbalances, recent works have proposed a logit-adjusted loss modification to standard empirical risk minimization. We show that this might be ineffective in general and, in particular so, in the overparameterized regime where training continues in the zero training-error regime. Specifically for binary linear classification of a separable dataset, we show that the modified loss converges to the max-margin SVM classifier despite the logit adjustment. Instead, we propose a more general vector-scaling loss that directly relates to the cost-sensitive SVM (CS-SVM), thus favoring larger margin to the minority class. Through an insightful sharp asymptotic analysis for a Gaussian-mixtures data model, we demonstrate the efficacy of CS-SVM in balancing the errors of the minority/majority classes. Our analysis also leads to a simple strategy for optimally tuning the involved margin-ratio parameter. Then, we show how our results extend naturally to binary classification with sensitive groups, thus treating the two common types of imbalances (label/group) in a unifying way. We corroborate our theoretical findings with numerical experiments on both synthetic and real-world datasets.

Sample Efficient Subspace-based Representations for Nonlinear Meta-Learning

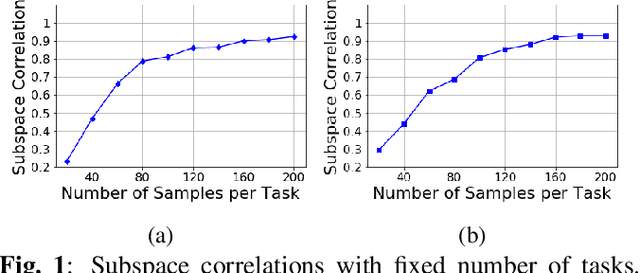
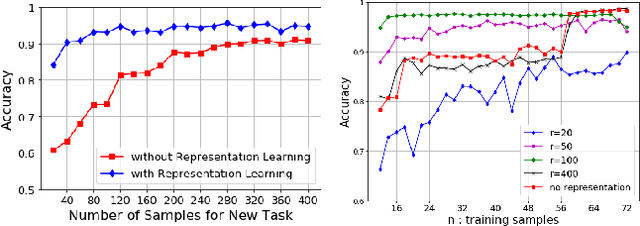
Constructing good representations is critical for learning complex tasks in a sample efficient manner. In the context of meta-learning, representations can be constructed from common patterns of previously seen tasks so that a future task can be learned quickly. While recent works show the benefit of subspace-based representations, such results are limited to linear-regression tasks. This work explores a more general class of nonlinear tasks with applications ranging from binary classification, generalized linear models and neural nets. We prove that subspace-based representations can be learned in a sample-efficient manner and provably benefit future tasks in terms of sample complexity. Numerical results verify the theoretical predictions in classification and neural-network regression tasks.

Super-Convergence with an Unstable Learning Rate

Conventional wisdom dictates that learning rate should be in the stable regime so that gradient-based algorithms don't blow up. This note introduces a simple scenario where an unstable learning rate scheme leads to a super fast convergence, with the convergence rate depending only logarithmically on the condition number of the problem. Our scheme uses a Cyclical Learning Rate where we periodically take one large unstable step and several small stable steps to compensate for the instability. These findings also help explain the empirical observations of [Smith and Topin, 2019] where they claim CLR with a large maximum learning rate leads to "super-convergence". We prove that our scheme excels in the problems where Hessian exhibits a bimodal spectrum and the eigenvalues can be grouped into two clusters (small and large). The unstable step is the key to enabling fast convergence over the small eigen-spectrum.

Provable Benefits of Overparameterization in Model Compression: From Double Descent to Pruning Neural Networks

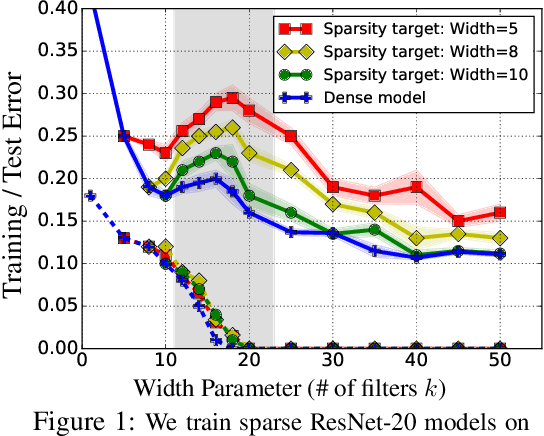
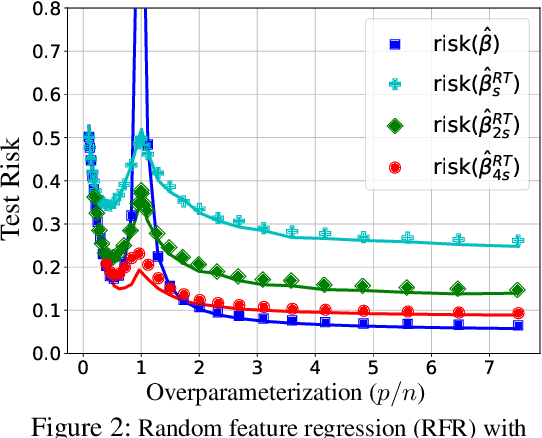
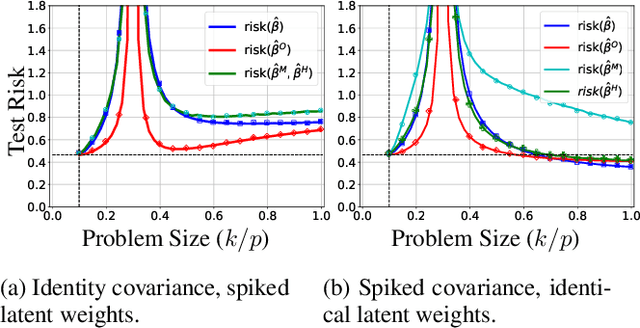
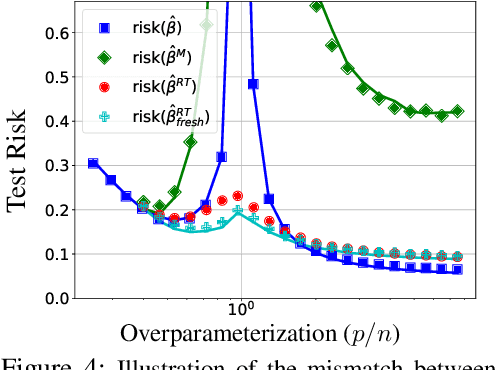
Deep networks are typically trained with many more parameters than the size of the training dataset. Recent empirical evidence indicates that the practice of overparameterization not only benefits training large models, but also assists - perhaps counterintuitively - building lightweight models. Specifically, it suggests that overparameterization benefits model pruning / sparsification. This paper sheds light on these empirical findings by theoretically characterizing the high-dimensional asymptotics of model pruning in the overparameterized regime. The theory presented addresses the following core question: "should one train a small model from the beginning, or first train a large model and then prune?". We analytically identify regimes in which, even if the location of the most informative features is known, we are better off fitting a large model and then pruning rather than simply training with the known informative features. This leads to a new double descent in the training of sparse models: growing the original model, while preserving the target sparsity, improves the test accuracy as one moves beyond the overparameterization threshold. Our analysis further reveals the benefit of retraining by relating it to feature correlations. We find that the above phenomena are already present in linear and random-features models. Our technical approach advances the toolset of high-dimensional analysis and precisely characterizes the asymptotic distribution of over-parameterized least-squares. The intuition gained by analytically studying simpler models is numerically verified on neural networks.

On the Marginal Benefit of Active Learning: Does Self-Supervision Eat Its Cake?

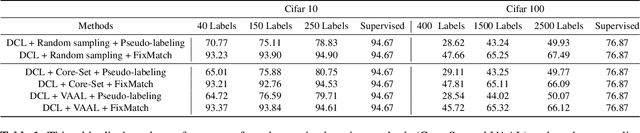
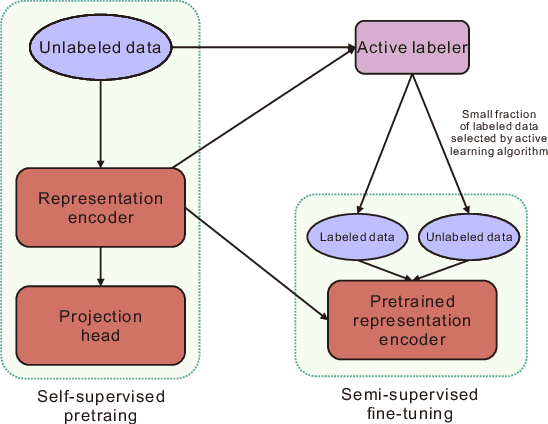
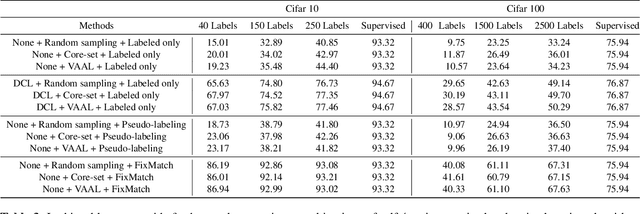
Active learning is the set of techniques for intelligently labeling large unlabeled datasets to reduce the labeling effort. In parallel, recent developments in self-supervised and semi-supervised learning (S4L) provide powerful techniques, based on data-augmentation, contrastive learning, and self-training, that enable superior utilization of unlabeled data which led to a significant reduction in required labeling in the standard machine learning benchmarks. A natural question is whether these paradigms can be unified to obtain superior results. To this aim, this paper provides a novel algorithmic framework integrating self-supervised pretraining, active learning, and consistency-regularized self-training. We conduct extensive experiments with our framework on CIFAR10 and CIFAR100 datasets. These experiments enable us to isolate and assess the benefits of individual components which are evaluated using state-of-the-art methods (e.g.~Core-Set, VAAL, simCLR, FixMatch). Our experiments reveal two key insights: (i) Self-supervised pre-training significantly improves semi-supervised learning, especially in the few-label regime, (ii) The benefit of active learning is undermined and subsumed by S4L techniques. Specifically, we fail to observe any additional benefit of state-of-the-art active learning algorithms when combined with state-of-the-art S4L techniques.