Distributional Training Data Attribution

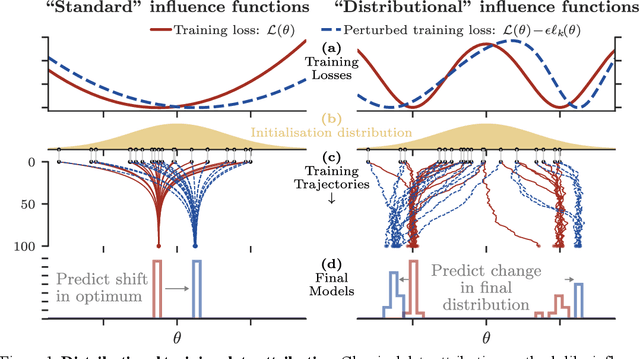
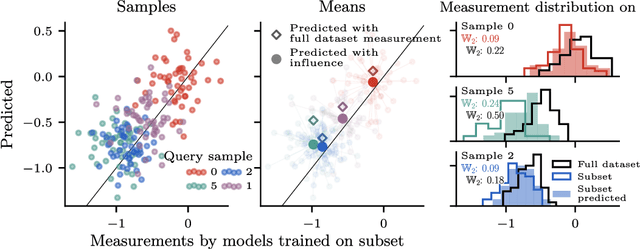
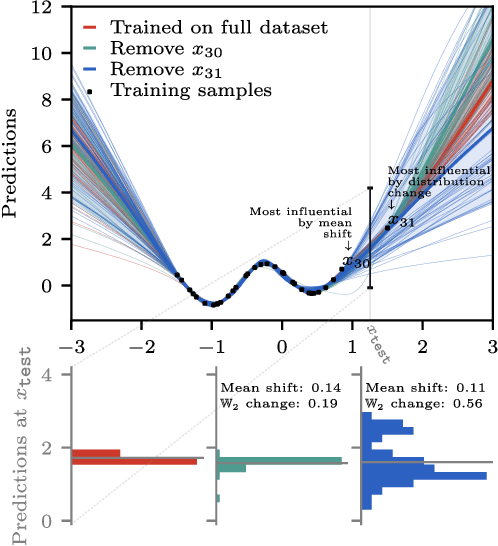
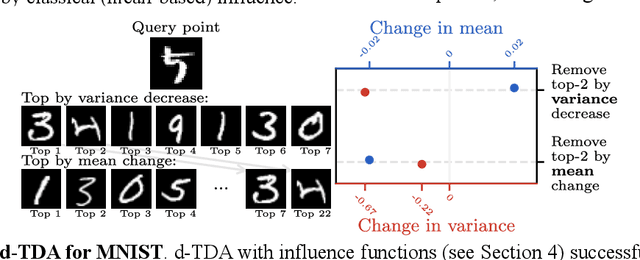
Randomness is an unavoidable part of training deep learning models, yet something that traditional training data attribution algorithms fail to rigorously account for. They ignore the fact that, due to stochasticity in the initialisation and batching, training on the same dataset can yield different models. In this paper, we address this shortcoming through introducing distributional training data attribution (d-TDA), the goal of which is to predict how the distribution of model outputs (over training runs) depends upon the dataset. We demonstrate the practical significance of d-TDA in experiments, e.g. by identifying training examples that drastically change the distribution of some target measurement without necessarily changing the mean. Intriguingly, we also find that influence functions (IFs), a popular but poorly-understood data attribution tool, emerge naturally from our distributional framework as the limit to unrolled differentiation; without requiring restrictive convexity assumptions. This provides a new mathematical motivation for their efficacy in deep learning, and helps to characterise their limitations.

Comparison of Markov chains via weak Poincaré inequalities with application to pseudo-marginal MCMC

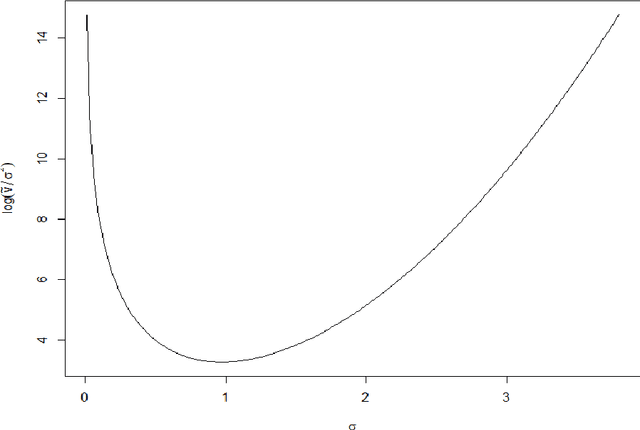
We investigate the use of a certain class of functional inequalities known as weak Poincar\'e inequalities to bound convergence of Markov chains to equilibrium. We show that this enables the straightforward and transparent derivation of subgeometric convergence bounds for methods such as the Independent Metropolis--Hastings sampler and pseudo-marginal methods for intractable likelihoods, the latter being subgeometric in many practical settings. These results rely on novel quantitative comparison theorems between Markov chains. Associated proofs are simpler than those relying on drift/minorization conditions and the tools developed allow us to recover and further extend known results as particular cases. We are then able to provide new insights into the practical use of pseudo-marginal algorithms, analyse the effect of averaging in Approximate Bayesian Computation (ABC) and the use of products of independent averages, and also to study the case of lognormal weights relevant to particle marginal Metropolis--Hastings (PMMH).