Distributional Training Data Attribution
Paper and Code
Jun 15, 2025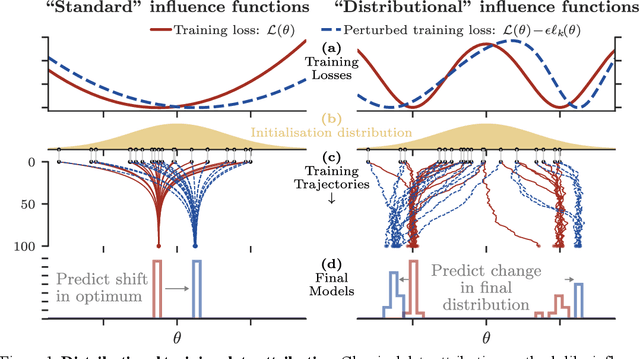
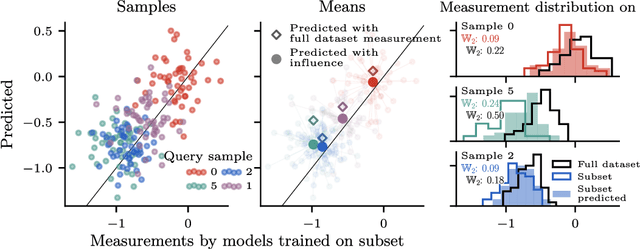
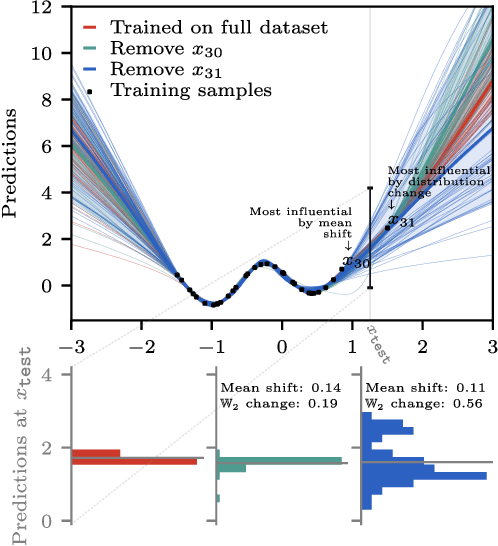
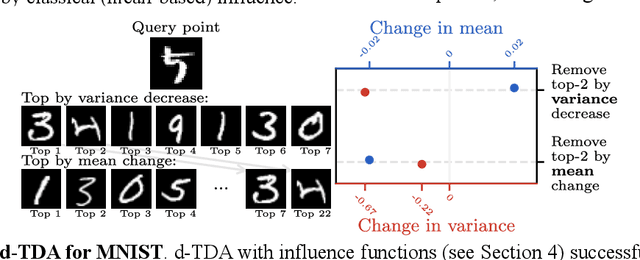
Randomness is an unavoidable part of training deep learning models, yet something that traditional training data attribution algorithms fail to rigorously account for. They ignore the fact that, due to stochasticity in the initialisation and batching, training on the same dataset can yield different models. In this paper, we address this shortcoming through introducing distributional training data attribution (d-TDA), the goal of which is to predict how the distribution of model outputs (over training runs) depends upon the dataset. We demonstrate the practical significance of d-TDA in experiments, e.g. by identifying training examples that drastically change the distribution of some target measurement without necessarily changing the mean. Intriguingly, we also find that influence functions (IFs), a popular but poorly-understood data attribution tool, emerge naturally from our distributional framework as the limit to unrolled differentiation; without requiring restrictive convexity assumptions. This provides a new mathematical motivation for their efficacy in deep learning, and helps to characterise their limitations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge