End-to-End Text-to-SQL with Dataset Selection: Leveraging LLMs for Adaptive Query Generation

Text-to-SQL bridges the gap between natural language and structured database language, thus allowing non-technical users to easily query databases. Traditional approaches model text-to-SQL as a direct translation task, where a given Natural Language Query (NLQ) is mapped to an SQL command. Recent advances in large language models (LLMs) have significantly improved translation accuracy, however, these methods all require that the target database is pre-specified. This becomes problematic in scenarios with multiple extensive databases, where identifying the correct database becomes a crucial yet overlooked step. In this paper, we propose a three-stage end-to-end text-to-SQL framework to identify the user's intended database before generating SQL queries. Our approach leverages LLMs and prompt engineering to extract implicit information from natural language queries (NLQs) in the form of a ruleset. We then train a large db\_id prediction model, which includes a RoBERTa-based finetuned encoder, to predict the correct Database identifier (db\_id) based on both the NLQ and the LLM-generated rules. Finally, we refine the generated SQL by using critic agents to correct errors. Experimental results demonstrate that our framework outperforms the current state-of-the-art models in both database intent prediction and SQL generation accuracy.

Quantum Extremal Learning

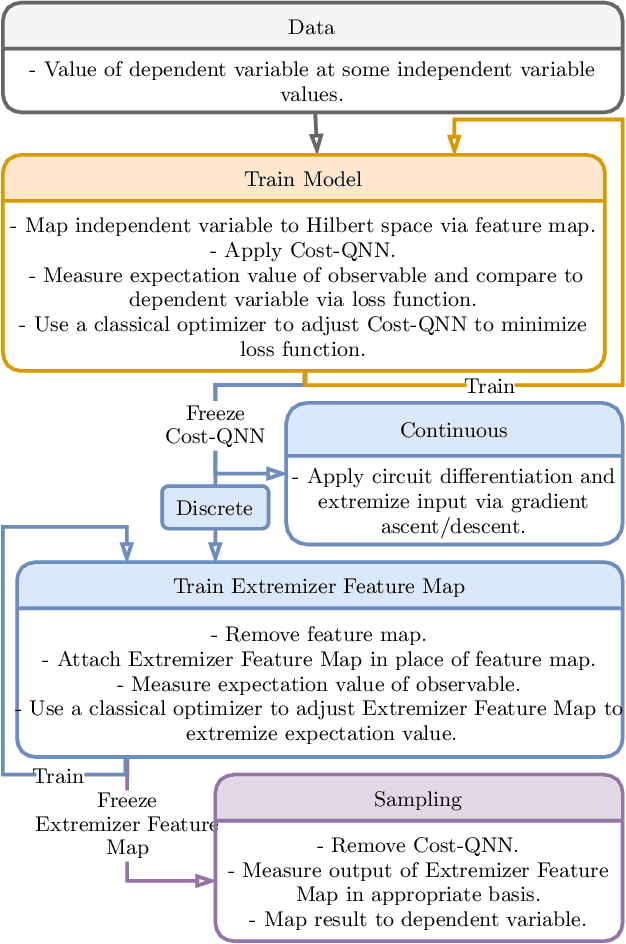
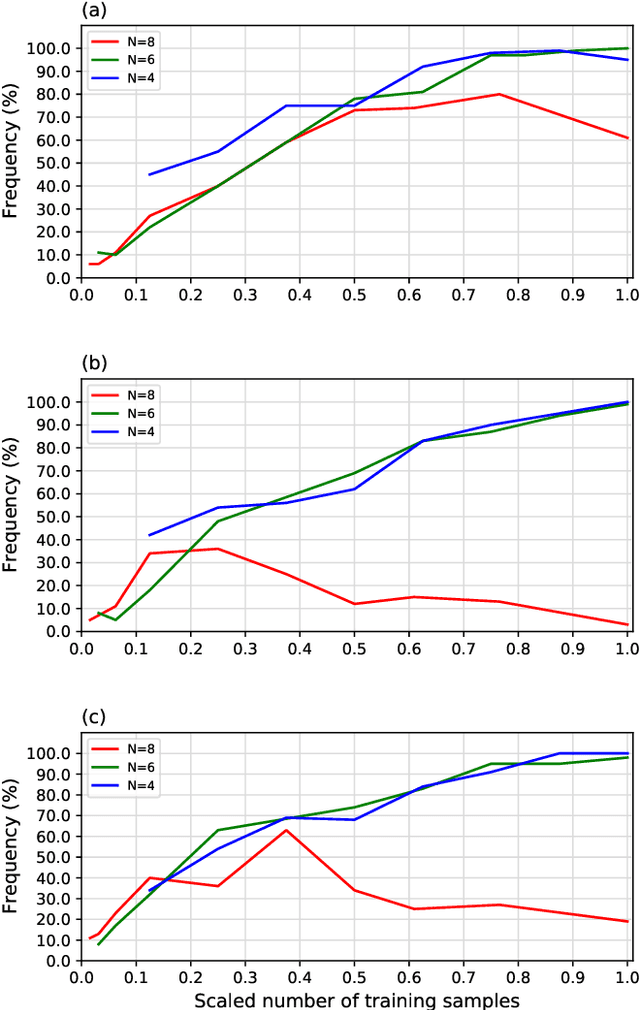
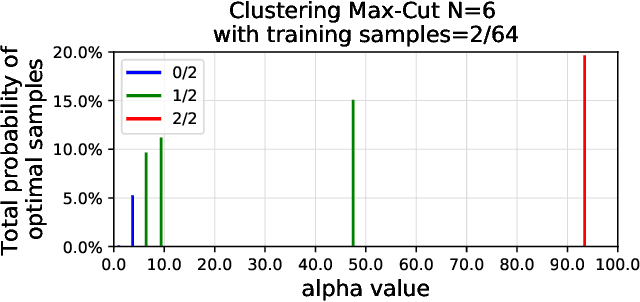
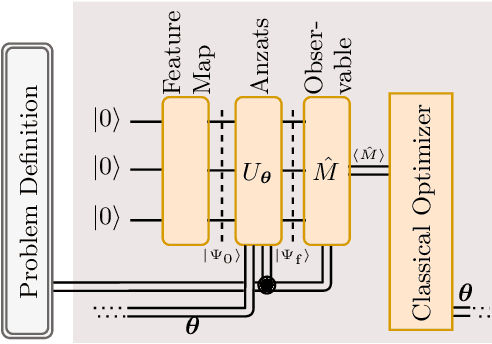
We propose a quantum algorithm for `extremal learning', which is the process of finding the input to a hidden function that extremizes the function output, without having direct access to the hidden function, given only partial input-output (training) data. The algorithm, called quantum extremal learning (QEL), consists of a parametric quantum circuit that is variationally trained to model data input-output relationships and where a trainable quantum feature map, that encodes the input data, is analytically differentiated in order to find the coordinate that extremizes the model. This enables the combination of established quantum machine learning modelling with established quantum optimization, on a single circuit/quantum computer. We have tested our algorithm on a range of classical datasets based on either discrete or continuous input variables, both of which are compatible with the algorithm. In case of discrete variables, we test our algorithm on synthetic problems formulated based on Max-Cut problem generators and also considering higher order correlations in the input-output relationships. In case of the continuous variables, we test our algorithm on synthetic datasets in 1D and simple ordinary differential functions. We find that the algorithm is able to successfully find the extremal value of such problems, even when the training dataset is sparse or a small fraction of the input configuration space. We additionally show how the algorithm can be used for much more general cases of higher dimensionality, complex differential equations, and with full flexibility in the choice of both modeling and optimization ansatz. We envision that due to its general framework and simple construction, the QEL algorithm will be able to solve a wide variety of applications in different fields, opening up areas of further research.