Quantum Extremal Learning

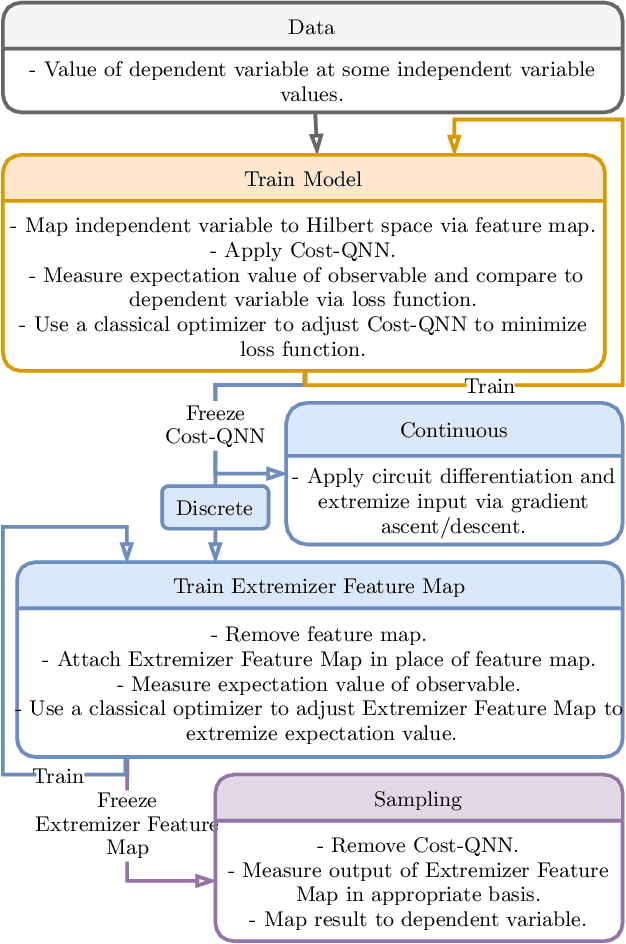
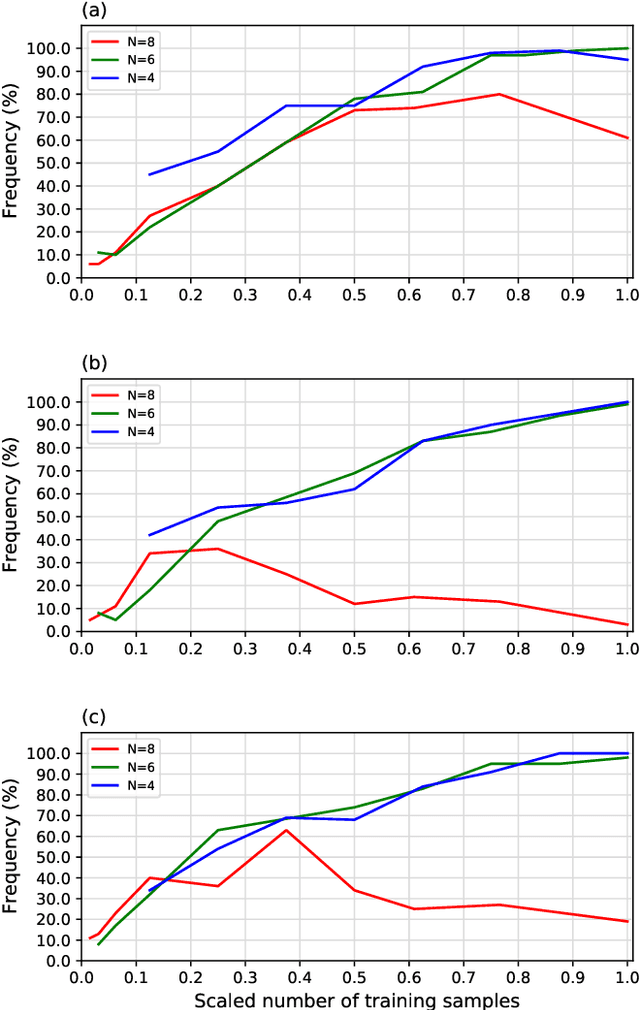
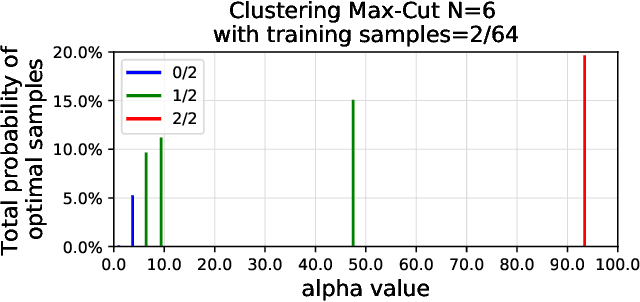
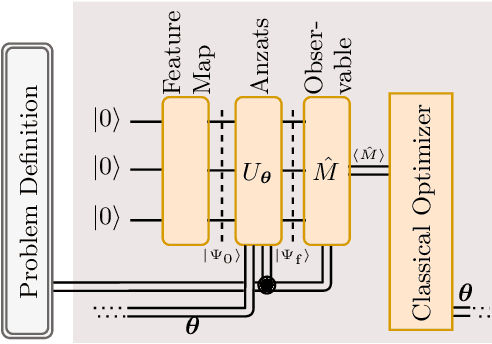
We propose a quantum algorithm for `extremal learning', which is the process of finding the input to a hidden function that extremizes the function output, without having direct access to the hidden function, given only partial input-output (training) data. The algorithm, called quantum extremal learning (QEL), consists of a parametric quantum circuit that is variationally trained to model data input-output relationships and where a trainable quantum feature map, that encodes the input data, is analytically differentiated in order to find the coordinate that extremizes the model. This enables the combination of established quantum machine learning modelling with established quantum optimization, on a single circuit/quantum computer. We have tested our algorithm on a range of classical datasets based on either discrete or continuous input variables, both of which are compatible with the algorithm. In case of discrete variables, we test our algorithm on synthetic problems formulated based on Max-Cut problem generators and also considering higher order correlations in the input-output relationships. In case of the continuous variables, we test our algorithm on synthetic datasets in 1D and simple ordinary differential functions. We find that the algorithm is able to successfully find the extremal value of such problems, even when the training dataset is sparse or a small fraction of the input configuration space. We additionally show how the algorithm can be used for much more general cases of higher dimensionality, complex differential equations, and with full flexibility in the choice of both modeling and optimization ansatz. We envision that due to its general framework and simple construction, the QEL algorithm will be able to solve a wide variety of applications in different fields, opening up areas of further research.

Modern Hopfield Networks for Few- and Zero-Shot Reaction Prediction

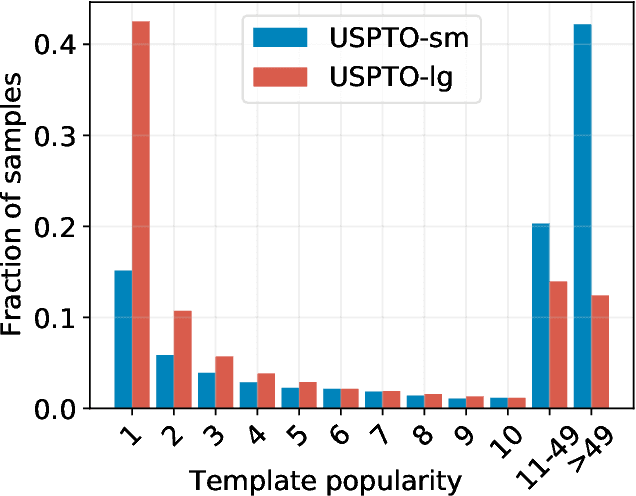
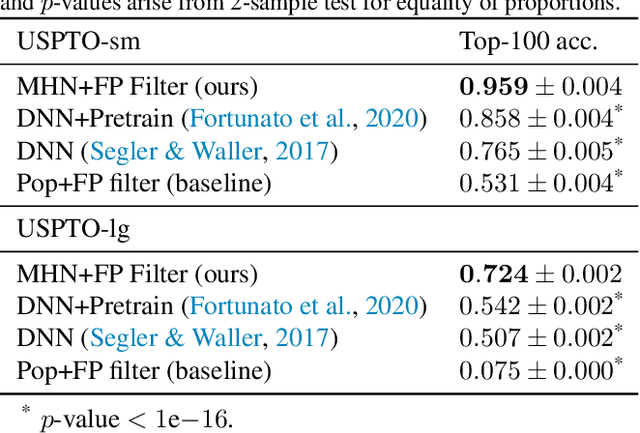
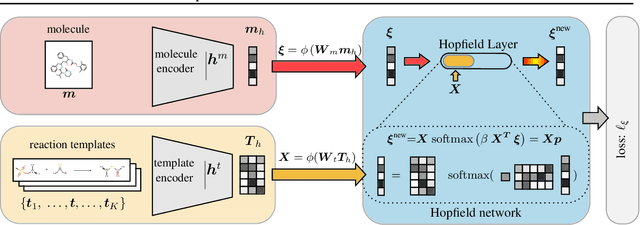
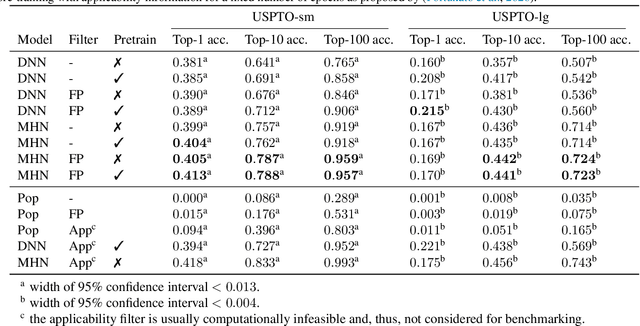
An essential step in the discovery of new drugs and materials is the synthesis of a molecule that exists so far only as an idea to test its biological and physical properties. While computer-aided design of virtual molecules has made large progress, computer-assisted synthesis planning (CASP) to realize physical molecules is still in its infancy and lacks a performance level that would enable large-scale molecule discovery. CASP supports the search for multi-step synthesis routes, which is very challenging due to high branching factors in each synthesis step and the hidden rules that govern the reactions. The central and repeatedly applied step in CASP is reaction prediction, for which machine learning methods yield the best performance. We propose a novel reaction prediction approach that uses a deep learning architecture with modern Hopfield networks (MHNs) that is optimized by contrastive learning. An MHN is an associative memory that can store and retrieve chemical reactions in each layer of a deep learning architecture. We show that our MHN contrastive learning approach enables few- and zero-shot learning for reaction prediction which, in contrast to previous methods, can deal with rare, single, or even no training example(s) for a reaction. On a well established benchmark, our MHN approach pushes the state-of-the-art performance up by a large margin as it improves the predictive top-100 accuracy from $0.858\pm0.004$ to $0.959\pm0.004$. This advance might pave the way to large-scale molecule discovery.