Experimental differentiation and extremization with analog quantum circuits

Solving and optimizing differential equations (DEs) is ubiquitous in both engineering and fundamental science. The promise of quantum architectures to accelerate scientific computing thus naturally involved interest towards how efficiently quantum algorithms can solve DEs. Differentiable quantum circuits (DQC) offer a viable route to compute DE solutions using a variational approach amenable to existing quantum computers, by producing a machine-learnable surrogate of the solution. Quantum extremal learning (QEL) complements such approach by finding extreme points in the output of learnable models of unknown (implicit) functions, offering a powerful tool to bypass a full DE solution, in cases where the crux consists in retrieving solution extrema. In this work, we provide the results from the first experimental demonstration of both DQC and QEL, displaying their performance on a synthetic usecase. Whilst both DQC and QEL are expected to require digital quantum hardware, we successfully challenge this assumption by running a closed-loop instance on a commercial analog quantum computer, based upon neutral atom technology.

Conservative quantum offline model-based optimization

Offline model-based optimization (MBO) refers to the task of optimizing a black-box objective function using only a fixed set of prior input-output data, without any active experimentation. Recent work has introduced quantum extremal learning (QEL), which leverages the expressive power of variational quantum circuits to learn accurate surrogate functions by training on a few data points. However, as widely studied in the classical machine learning literature, predictive models may incorrectly extrapolate objective values in unexplored regions, leading to the selection of overly optimistic solutions. In this paper, we propose integrating QEL with conservative objective models (COM) - a regularization technique aimed at ensuring cautious predictions on out-of-distribution inputs. The resulting hybrid algorithm, COM-QEL, builds on the expressive power of quantum neural networks while safeguarding generalization via conservative modeling. Empirical results on benchmark optimization tasks demonstrate that COM-QEL reliably finds solutions with higher true objective values compared to the original QEL, validating its superiority for offline design problems.

Quantum Extremal Learning

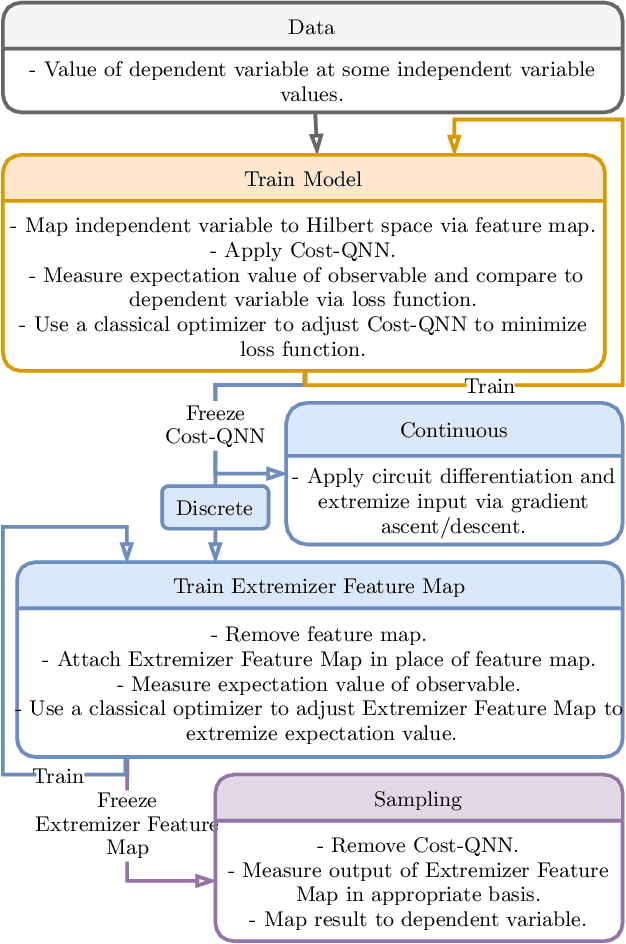
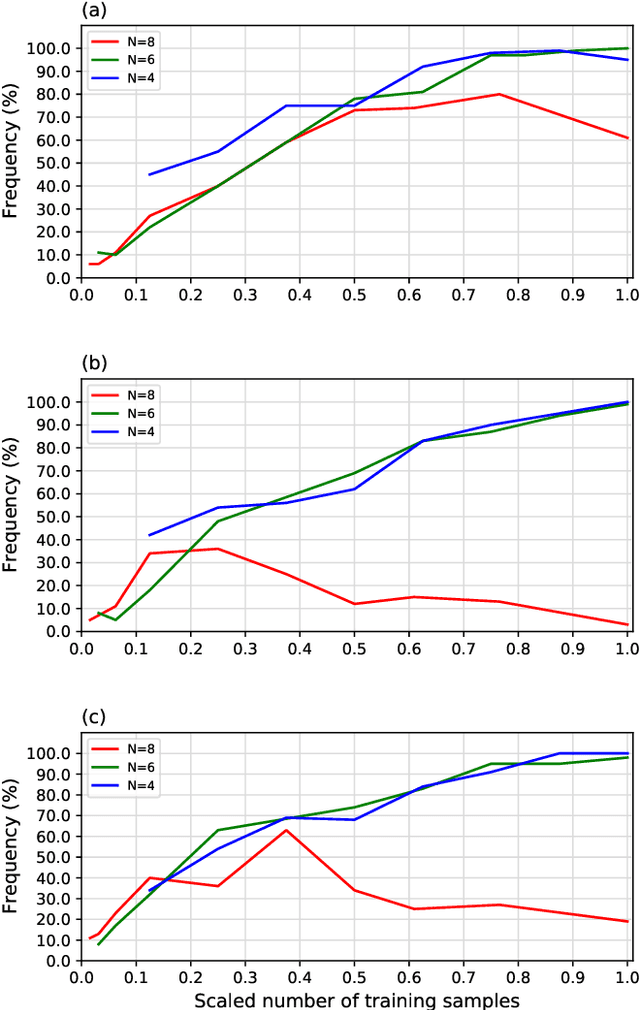
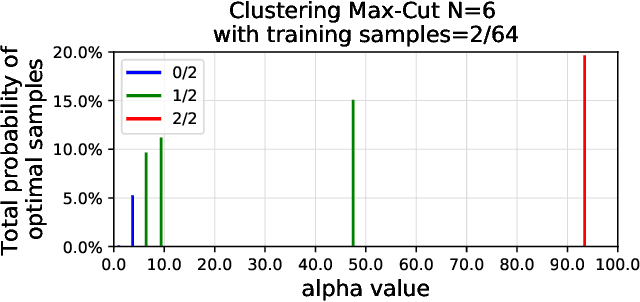
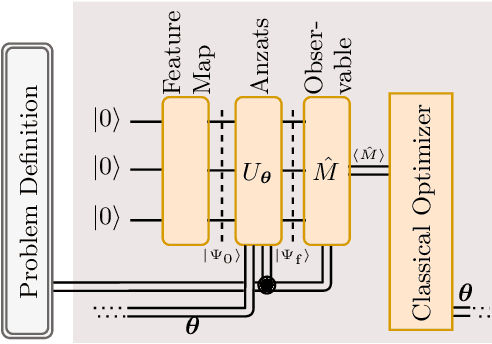
We propose a quantum algorithm for `extremal learning', which is the process of finding the input to a hidden function that extremizes the function output, without having direct access to the hidden function, given only partial input-output (training) data. The algorithm, called quantum extremal learning (QEL), consists of a parametric quantum circuit that is variationally trained to model data input-output relationships and where a trainable quantum feature map, that encodes the input data, is analytically differentiated in order to find the coordinate that extremizes the model. This enables the combination of established quantum machine learning modelling with established quantum optimization, on a single circuit/quantum computer. We have tested our algorithm on a range of classical datasets based on either discrete or continuous input variables, both of which are compatible with the algorithm. In case of discrete variables, we test our algorithm on synthetic problems formulated based on Max-Cut problem generators and also considering higher order correlations in the input-output relationships. In case of the continuous variables, we test our algorithm on synthetic datasets in 1D and simple ordinary differential functions. We find that the algorithm is able to successfully find the extremal value of such problems, even when the training dataset is sparse or a small fraction of the input configuration space. We additionally show how the algorithm can be used for much more general cases of higher dimensionality, complex differential equations, and with full flexibility in the choice of both modeling and optimization ansatz. We envision that due to its general framework and simple construction, the QEL algorithm will be able to solve a wide variety of applications in different fields, opening up areas of further research.