A Method for Handling Negative Similarities in Explainable Graph Spectral Clustering of Text Documents -- Extended Version

This paper investigates the problem of Graph Spectral Clustering with negative similarities, resulting from document embeddings different from the traditional Term Vector Space (like doc2vec, GloVe, etc.). Solutions for combinatorial Laplacians and normalized Laplacians are discussed. An experimental investigation shows the advantages and disadvantages of 6 different solutions proposed in the literature and in this research. The research demonstrates that GloVe embeddings frequently cause failures of normalized Laplacian based GSC due to negative similarities. Furthermore, application of methods curing similarity negativity leads to accuracy improvement for both combinatorial and normalized Laplacian based GSC. It also leads to applicability for GloVe embeddings of explanation methods developed originally bythe authors for Term Vector Space embeddings.

Eigenvalue-based Incremental Spectral Clustering

Our previous experiments demonstrated that subsets collections of (short) documents (with several hundred entries) share a common normalized in some way eigenvalue spectrum of combinatorial Laplacian. Based on this insight, we propose a method of incremental spectral clustering. The method consists of the following steps: (1) split the data into manageable subsets, (2) cluster each of the subsets, (3) merge clusters from different subsets based on the eigenvalue spectrum similarity to form clusters of the entire set. This method can be especially useful for clustering methods of complexity strongly increasing with the size of the data sample,like in case of typical spectral clustering. Experiments were performed showing that in fact the clustering and merging the subsets yields clusters close to clustering the entire dataset.

Explainable Graph Spectral Clustering of Text Documents

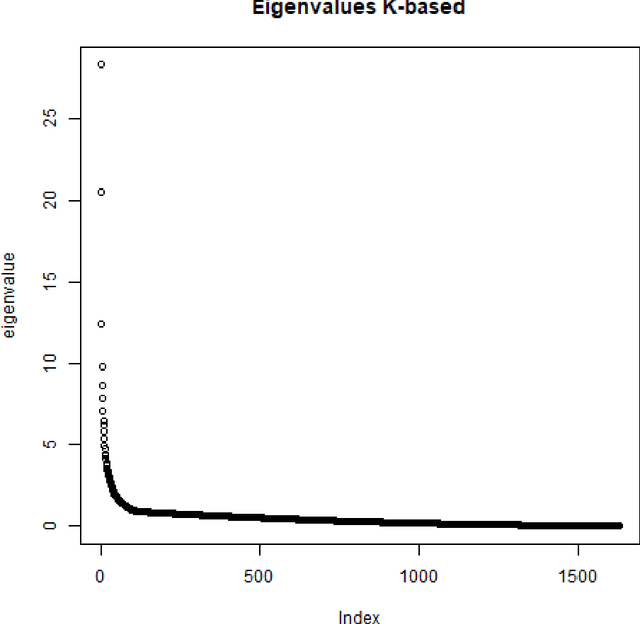
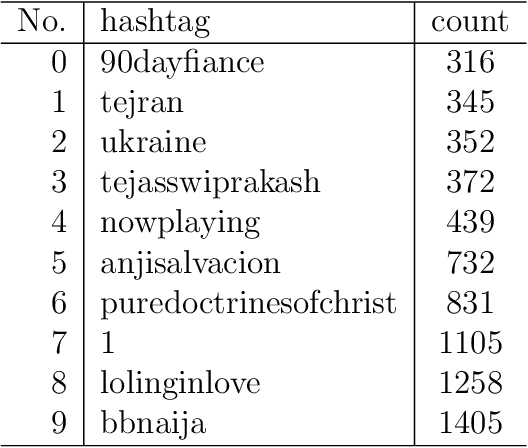
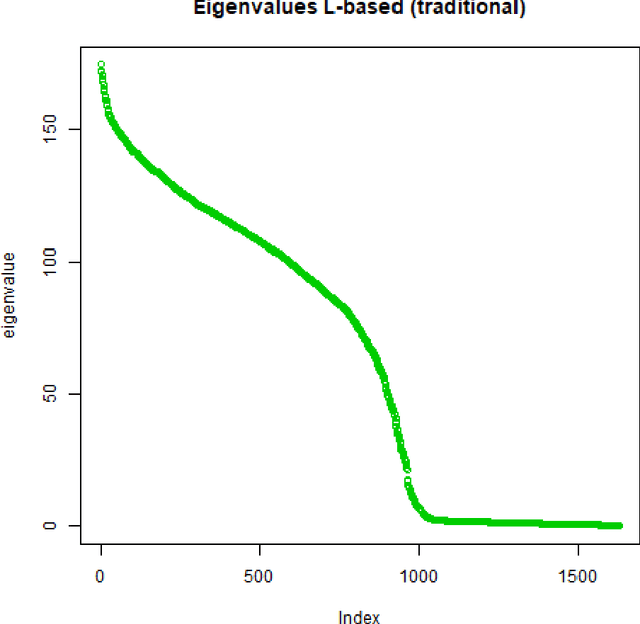
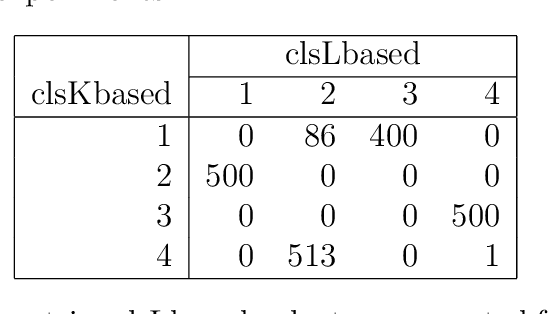
Spectral clustering methods are known for their ability to represent clusters of diverse shapes, densities etc. However, results of such algorithms, when applied e.g. to text documents, are hard to explain to the user, especially due to embedding in the spectral space which has no obvious relation to document contents. Therefore there is an urgent need to elaborate methods for explaining the outcome of the clustering. This paper presents a contribution towards this goal. We present a proposal of explanation of results of combinatorial Laplacian based graph spectral clustering. It is based on showing (approximate) equivalence of combinatorial Laplacian embedding, $K$-embedding (proposed in this paper) and term vector space embedding. Hence a bridge is constructed between the textual contents and the clustering results. We provide theoretical background for this approach. We performed experimental study showing that $K$-embedding approximates well Laplacian embedding under favourable block matrix conditions and show that approximation is good enough under other conditions.

Query Optimization Properties of Modified VBS

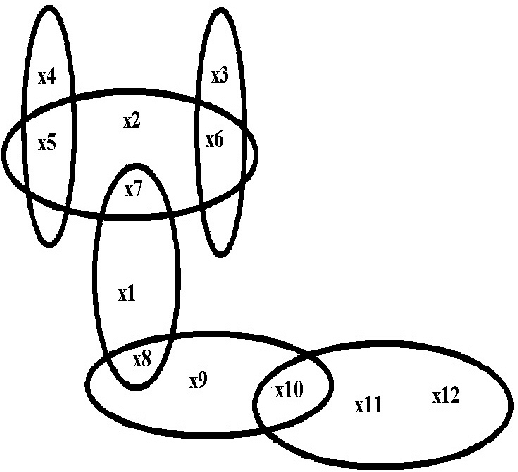
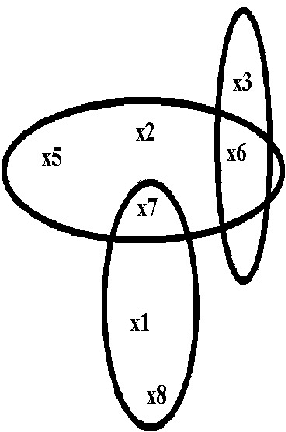
Valuation-Based~System can represent knowledge in different domains including probability theory, Dempster-Shafer theory and possibility theory. More recent studies show that the framework of VBS is also appropriate for representing and solving Bayesian decision problems and optimization problems. In this paper after introducing the valuation based system (VBS) framework, we present Markov-like properties of VBS and a method for resolving queries to VBS.

On Marginally Correct Approximations of Dempster-Shafer Belief Functions from Data

Mathematical Theory of Evidence (MTE), a foundation for reasoning under partial ignorance, is blamed to leave frequencies outside (or aside of) its framework. The seriousness of this accusation is obvious: no experiment may be run to compare the performance of MTE-based models of real world processes against real world data. In this paper we consider this problem from the point of view of conditioning in the MTE. We describe the class of belief functions for which marginal consistency with observed frequencies may be achieved and conditional belief functions are proper belief functions,%\ and deal with implications for (marginal) approximation of general belief functions by this class of belief functions and for inference models in MTE.

Basic Formal Properties of A Relational Model of The Mathematical Theory of Evidence

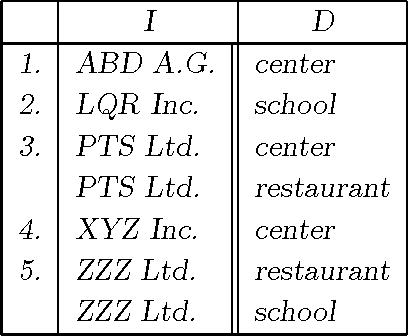
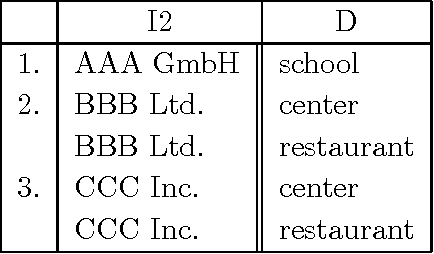
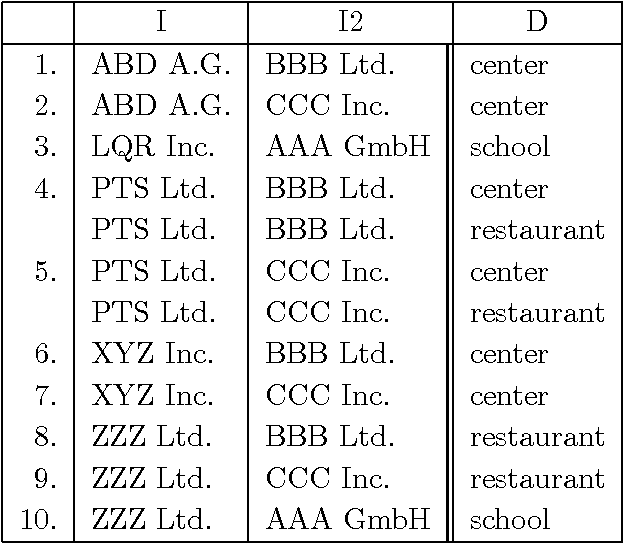
The paper presents a novel view of the Dempster-Shafer belief function as a measure of diversity in relational data bases. It is demonstrated that under the interpretation The Dempster rule of evidence combination corresponds to the join operator of the relational database theory. This rough-set based interpretation is qualitative in nature and can represent a number of belief function operators. The interpretation has the property that Given a definition of the belief measure of objects in the interpretation domain we can perform operations in this domain and the measure of the resulting object is derivable from measures of component objects via belief operator. We demonstrated this property for Dempster rule of combination, marginalization, Shafer's conditioning, independent variables, Shenoy's notion of conditional independence of variables. The interpretation is based on rough sets (in connection with decision tables), but differs from previous interpretations of this type in that it counts the diversity rather than frequencies in a decision table.