A Method for Handling Negative Similarities in Explainable Graph Spectral Clustering of Text Documents -- Extended Version

This paper investigates the problem of Graph Spectral Clustering with negative similarities, resulting from document embeddings different from the traditional Term Vector Space (like doc2vec, GloVe, etc.). Solutions for combinatorial Laplacians and normalized Laplacians are discussed. An experimental investigation shows the advantages and disadvantages of 6 different solutions proposed in the literature and in this research. The research demonstrates that GloVe embeddings frequently cause failures of normalized Laplacian based GSC due to negative similarities. Furthermore, application of methods curing similarity negativity leads to accuracy improvement for both combinatorial and normalized Laplacian based GSC. It also leads to applicability for GloVe embeddings of explanation methods developed originally bythe authors for Term Vector Space embeddings.

Eigenvalue-based Incremental Spectral Clustering

Our previous experiments demonstrated that subsets collections of (short) documents (with several hundred entries) share a common normalized in some way eigenvalue spectrum of combinatorial Laplacian. Based on this insight, we propose a method of incremental spectral clustering. The method consists of the following steps: (1) split the data into manageable subsets, (2) cluster each of the subsets, (3) merge clusters from different subsets based on the eigenvalue spectrum similarity to form clusters of the entire set. This method can be especially useful for clustering methods of complexity strongly increasing with the size of the data sample,like in case of typical spectral clustering. Experiments were performed showing that in fact the clustering and merging the subsets yields clusters close to clustering the entire dataset.

Wide Gaps and Clustering Axioms

The widely applied k-means algorithm produces clusterings that violate our expectations with respect to high/low similarity/density and is in conflict with Kleinberg's axiomatic system for distance based clustering algorithms that formalizes those expectations in a natural way. k-means violates in particular the consistency axiom. We hypothesise that this clash is due to the not explicated expectation that the data themselves should have the property of being clusterable in order to expect the algorithm clustering hem to fit a clustering axiomatic system. To demonstrate this, we introduce two new clusterability properties, variational k-separability and residual k-separability and show that then the Kleinberg's consistency axiom holds for k-means operating in the Euclidean or non-Euclidean space. Furthermore, we propose extensions of k-means algorithm that fit approximately the Kleinberg's richness axiom that does not hold for k-means. In this way, we reconcile k-means with Kleinberg's axiomatic framework in Euclidean and non-Euclidean settings. Besides contribution to the theory of axiomatic frameworks of clustering and for clusterability theory, practical contribution is the possibility to construct {datasets for testing purposes of algorithms optimizing k-means cost function. This includes a method of construction of {clusterable data with known in advance global optimum.

Are Easy Data Easy (for K-Means)

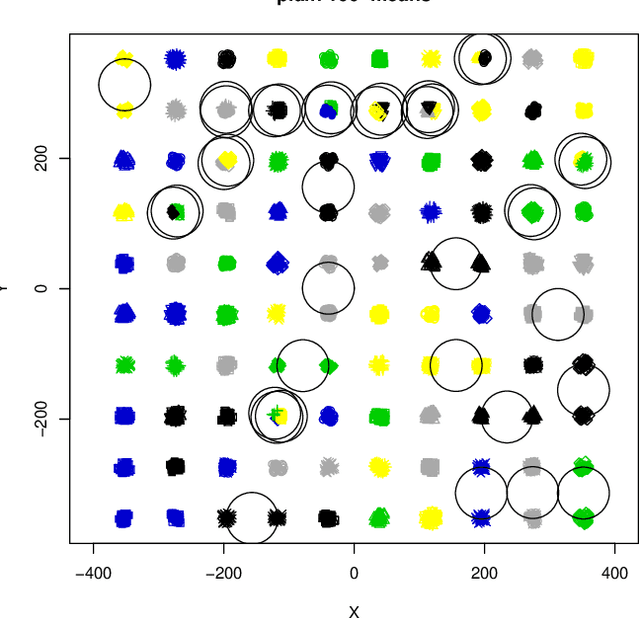
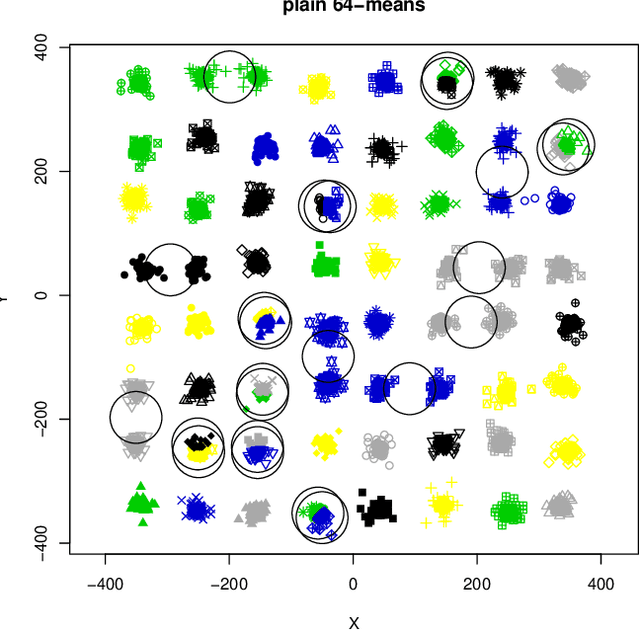
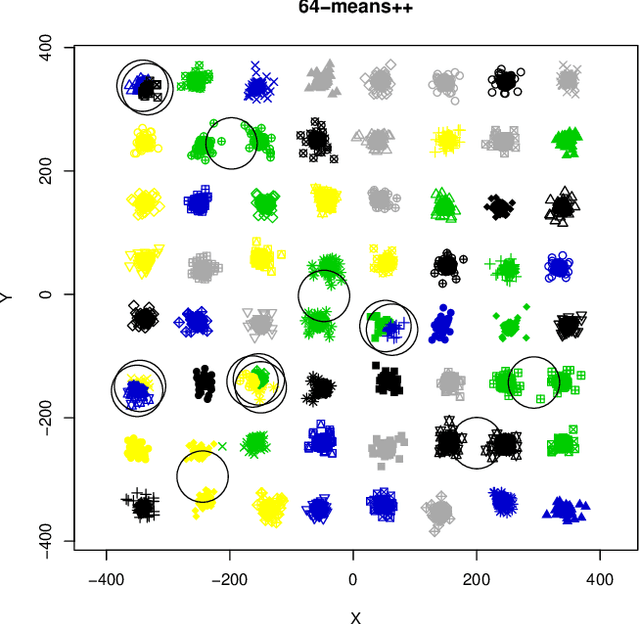
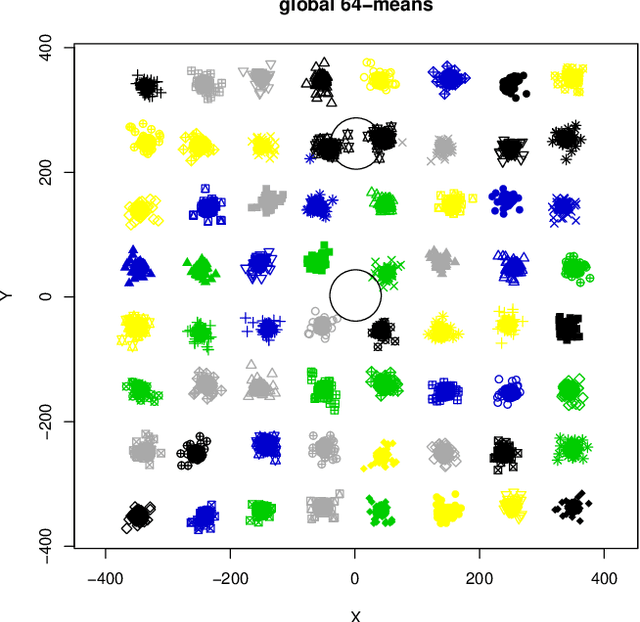
This paper investigates the capability of correctly recovering well-separated clusters by various brands of the $k$-means algorithm. The concept of well-separatedness used here is derived directly from the common definition of clusters, which imposes an interplay between the requirements of within-cluster-homogenicity and between-clusters-diversity. Conditions are derived for a special case of well-separated clusters such that the global minimum of $k$-means cost function coincides with the well-separatedness. An experimental investigation is performed to find out whether or no various brands of $k$-means are actually capable of discovering well separated clusters. It turns out that they are not. A new algorithm is proposed that is a variation of $k$-means++ via repeated {sub}sampling when choosing a seed. The new algorithm outperforms four other algorithms from $k$-means family on the task.

Explainable Graph Spectral Clustering of Text Documents

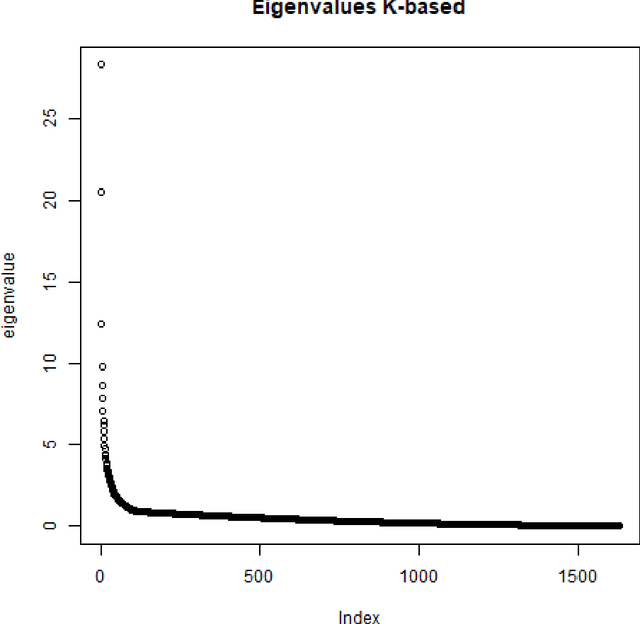
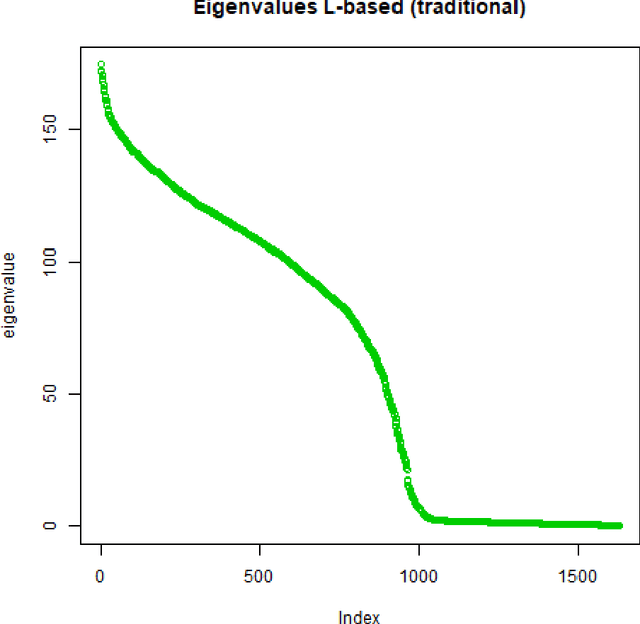
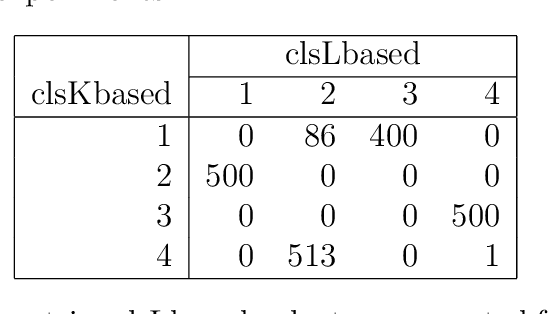
Spectral clustering methods are known for their ability to represent clusters of diverse shapes, densities etc. However, results of such algorithms, when applied e.g. to text documents, are hard to explain to the user, especially due to embedding in the spectral space which has no obvious relation to document contents. Therefore there is an urgent need to elaborate methods for explaining the outcome of the clustering. This paper presents a contribution towards this goal. We present a proposal of explanation of results of combinatorial Laplacian based graph spectral clustering. It is based on showing (approximate) equivalence of combinatorial Laplacian embedding, $K$-embedding (proposed in this paper) and term vector space embedding. Hence a bridge is constructed between the textual contents and the clustering results. We provide theoretical background for this approach. We performed experimental study showing that $K$-embedding approximates well Laplacian embedding under favourable block matrix conditions and show that approximation is good enough under other conditions.

High-Dimensional Wide Gap $k$-Means Versus Clustering Axioms

Kleinberg's axioms for distance based clustering proved to be contradictory. Various efforts have been made to overcome this problem. Here we make an attempt to handle the issue by embedding in high-dimensional space and granting wide gaps between clusters.

How To Overcome Richness Axiom Fallacy

The paper points at the grieving problems implied by the richness axiom in the Kleinberg's axiomatic system and suggests resolutions. The richness induces learnability problem in general and leads to conflicts with consistency axiom. As a resolution, learnability constraints and usage of centric consistency or restriction of the domain of considered clusterings to super-ball-clusterings is proposed.

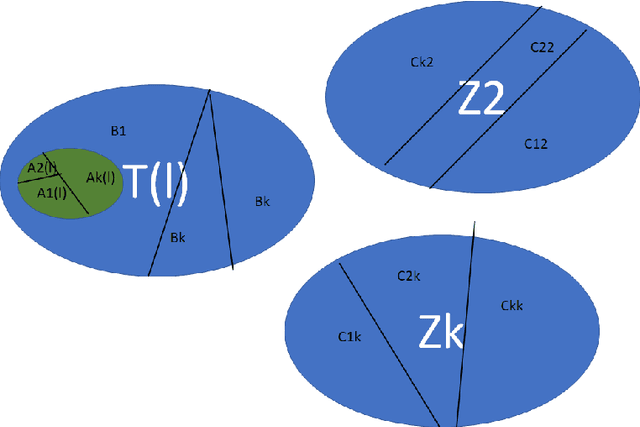
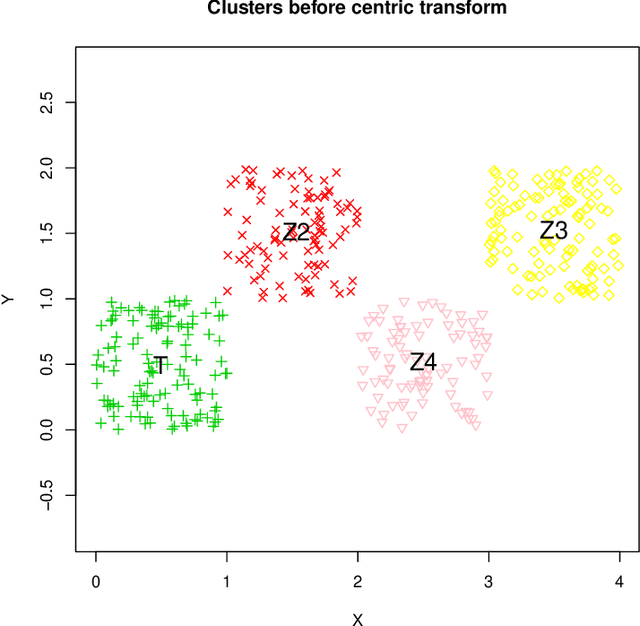
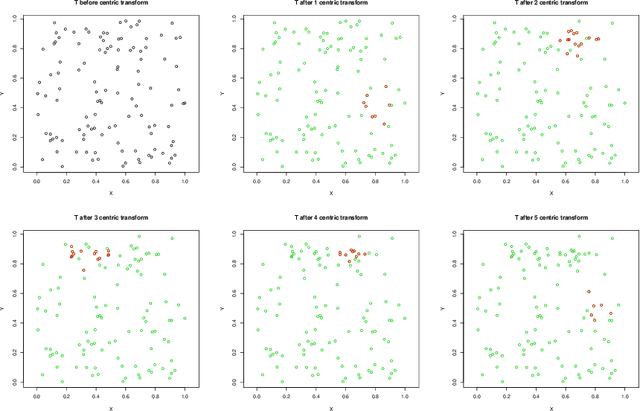
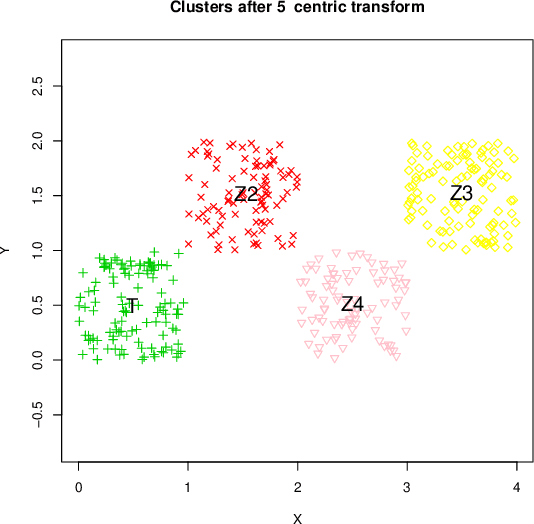
A Clustering Preserving Transformation for k-Means Algorithm Output

This note introduces a novel clustering preserving transformation of cluster sets obtained from $k$-means algorithm. This transformation may be used to generate new labeled data{}sets from existent ones. It is more flexible that Kleinberg axiom based consistency transformation because data points in a cluster can be moved away and datapoints between clusters may come closer together.

p-d-Separation -- A Concept for Expressing Dependence/Independence Relations in Causal Networks

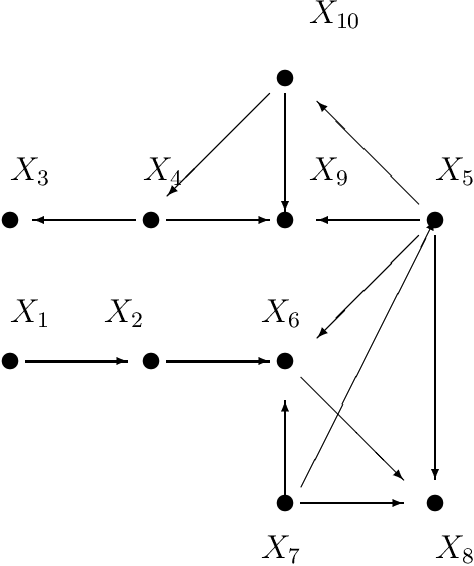
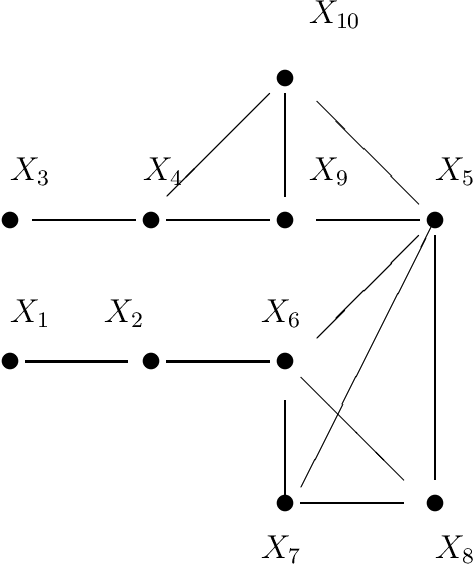
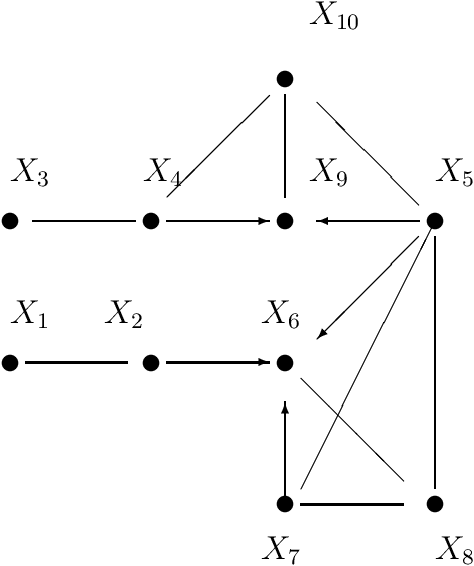
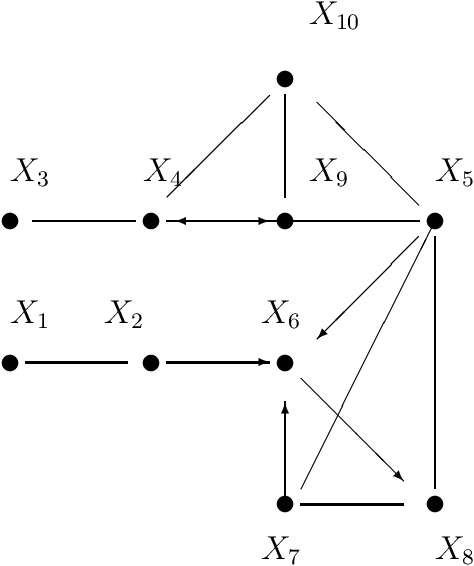
Spirtes, Glymour and Scheines formulated a Conjecture that a direct dependence test and a head-to-head meeting test would suffice to construe directed acyclic graph decompositions of a joint probability distribution (Bayesian network) for which Pearl's d-separation applies. This Conjecture was later shown to be a direct consequence of a result of Pearl and Verma. This paper is intended to prove this Conjecture in a new way, by exploiting the concept of p-d-separation (partial dependency separation). While Pearl's d-separation works with Bayesian networks, p-d-separation is intended to apply to causal networks: that is partially oriented networks in which orientations are given to only to those edges, that express statistically confirmed causal influence, whereas undirected edges express existence of direct influence without possibility of determination of direction of causation. As a consequence of the particular way of proving the validity of this Conjecture, an algorithm for construction of all the directed acyclic graphs (dags) carrying the available independence information is also presented. The notion of a partially oriented graph (pog) is introduced and within this graph the notion of p-d-separation is defined. It is demonstrated that the p-d-separation within the pog is equivalent to d-separation in all derived dags.

Non-Destructive Sample Generation From Conditional Belief Functions

This paper presents a new approach to generate samples from conditional belief functions for a restricted but non trivial subset of conditional belief functions. It assumes the factorization (decomposition) of a belief function along a bayesian network structure. It applies general conditional belief functions.