How many classifiers do we need?

As performance gains through scaling data and/or model size experience diminishing returns, it is becoming increasingly popular to turn to ensembling, where the predictions of multiple models are combined to improve accuracy. In this paper, we provide a detailed analysis of how the disagreement and the polarization (a notion we introduce and define in this paper) among classifiers relate to the performance gain achieved by aggregating individual classifiers, for majority vote strategies in classification tasks. We address these questions in the following ways. (1) An upper bound for polarization is derived, and we propose what we call a neural polarization law: most interpolating neural network models are 4/3-polarized. Our empirical results not only support this conjecture but also show that polarization is nearly constant for a dataset, regardless of hyperparameters or architectures of classifiers. (2) The error of the majority vote classifier is considered under restricted entropy conditions, and we present a tight upper bound that indicates that the disagreement is linearly correlated with the target, and that the slope is linear in the polarization. (3) We prove results for the asymptotic behavior of the disagreement in terms of the number of classifiers, which we show can help in predicting the performance for a larger number of classifiers from that of a smaller number. Our theories and claims are supported by empirical results on several image classification tasks with various types of neural networks.

Preference Optimization for Molecular Language Models

Molecular language modeling is an effective approach to generating novel chemical structures. However, these models do not \emph{a priori} encode certain preferences a chemist may desire. We investigate the use of fine-tuning using Direct Preference Optimization to better align generated molecules with chemist preferences. Our findings suggest that this approach is simple, efficient, and highly effective.

When are ensembles really effective?

Ensembling has a long history in statistical data analysis, with many impactful applications. However, in many modern machine learning settings, the benefits of ensembling are less ubiquitous and less obvious. We study, both theoretically and empirically, the fundamental question of when ensembling yields significant performance improvements in classification tasks. Theoretically, we prove new results relating the \emph{ensemble improvement rate} (a measure of how much ensembling decreases the error rate versus a single model, on a relative scale) to the \emph{disagreement-error ratio}. We show that ensembling improves performance significantly whenever the disagreement rate is large relative to the average error rate; and that, conversely, one classifier is often enough whenever the disagreement rate is low relative to the average error rate. On the way to proving these results, we derive, under a mild condition called \emph{competence}, improved upper and lower bounds on the average test error rate of the majority vote classifier. To complement this theory, we study ensembling empirically in a variety of settings, verifying the predictions made by our theory, and identifying practical scenarios where ensembling does and does not result in large performance improvements. Perhaps most notably, we demonstrate a distinct difference in behavior between interpolating models (popular in current practice) and non-interpolating models (such as tree-based methods, where ensembling is popular), demonstrating that ensembling helps considerably more in the latter case than in the former.

Evaluating natural language processing models with generalization metrics that do not need access to any training or testing data

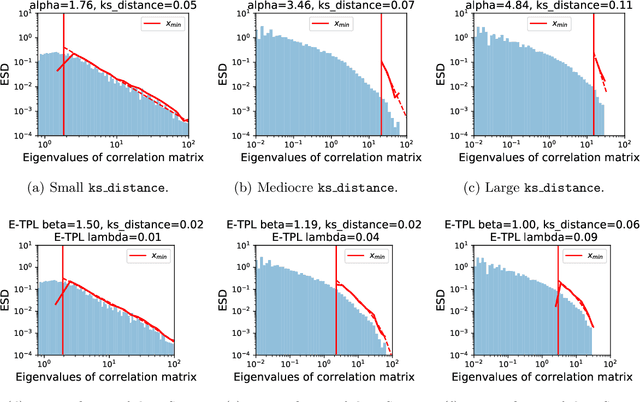
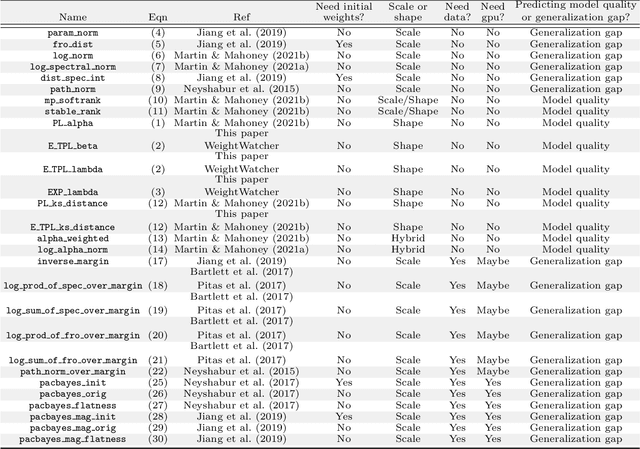
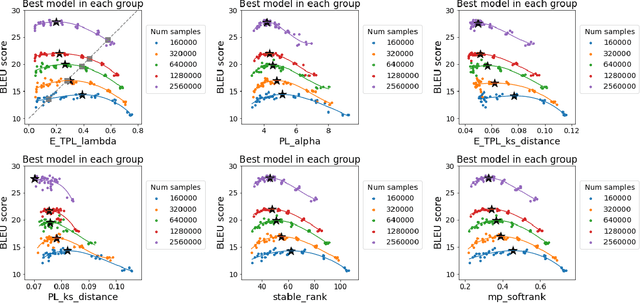
The search for effective and robust generalization metrics has been the focus of recent theoretical and empirical work. In this paper, we discuss the performance of natural language processing (NLP) models, and we evaluate various existing and novel generalization metrics. Compared to prior studies, we (i) focus on NLP instead of computer vision (CV), (ii) focus on generalization metrics that predict test error instead of the generalization gap, (iii) focus on generalization metrics that do not need the access to data, and (iv) focus on the heavy-tail (HT) phenomenon that has received comparatively less attention in the study of deep neural networks (NNs). We extend recent HT-based work which focuses on power law (PL) distributions, and we study exponential (EXP) and exponentially truncated power law (E-TPL) fitting to the empirical spectral densities (ESDs) of weight matrices. Our detailed empirical studies show that (i) \emph{shape metrics}, or the metrics obtained from fitting the shape of the ESDs, perform uniformly better at predicting generalization performance than \emph{scale metrics} commonly studied in the literature, as measured by the \emph{average} rank correlations with the generalization performance for all of our experiments; (ii) among forty generalization metrics studied in our paper, the \RANDDISTANCE metric, a new shape metric invented in this paper that measures the distance between empirical eigenvalues of weight matrices and those of randomly initialized weight matrices, achieves the highest worst-case rank correlation with generalization performance under a variety of training settings; and (iii) among the three HT distributions considered in our paper, the E-TPL fitting of ESDs performs the most robustly.

Taxonomizing local versus global structure in neural network loss landscapes

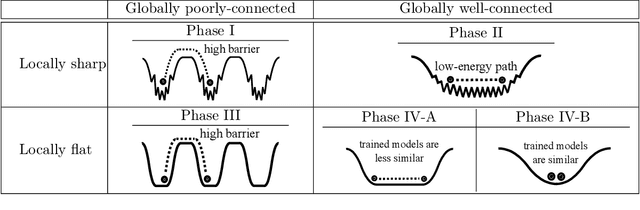
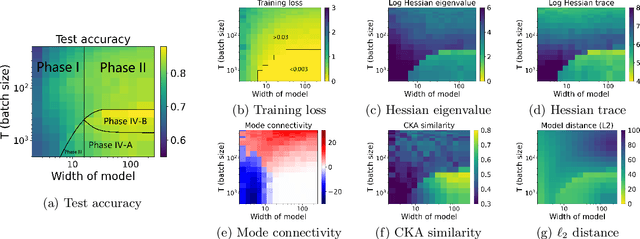
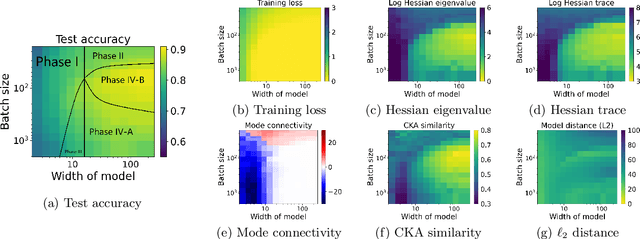
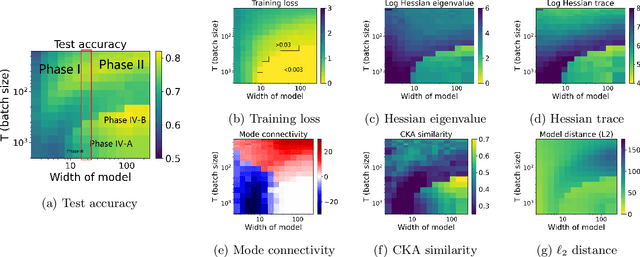
Viewing neural network models in terms of their loss landscapes has a long history in the statistical mechanics approach to learning, and in recent years it has received attention within machine learning proper. Among other things, local metrics (such as the smoothness of the loss landscape) have been shown to correlate with global properties of the model (such as good generalization). Here, we perform a detailed empirical analysis of the loss landscape structure of thousands of neural network models, systematically varying learning tasks, model architectures, and/or quantity/quality of data. By considering a range of metrics that attempt to capture different aspects of the loss landscape, we demonstrate that the best test accuracy is obtained when: the loss landscape is globally well-connected; ensembles of trained models are more similar to each other; and models converge to locally smooth regions. We also show that globally poorly-connected landscapes can arise when models are small or when they are trained to lower quality data; and that, if the loss landscape is globally poorly-connected, then training to zero loss can actually lead to worse test accuracy. Based on these results, we develop a simple one-dimensional model with load-like and temperature-like parameters, we introduce the notion of an \emph{effective loss landscape} depending on these parameters, and we interpret our results in terms of a \emph{rugged convexity} of the loss landscape. When viewed through this lens, our detailed empirical results shed light on phases of learning (and consequent double descent behavior), fundamental versus incidental determinants of good generalization, the role of load-like and temperature-like parameters in the learning process, different influences on the loss landscape from model and data, and the relationships between local and global metrics, all topics of recent interest.

Evaluating State-of-the-Art Classification Models Against Bayes Optimality

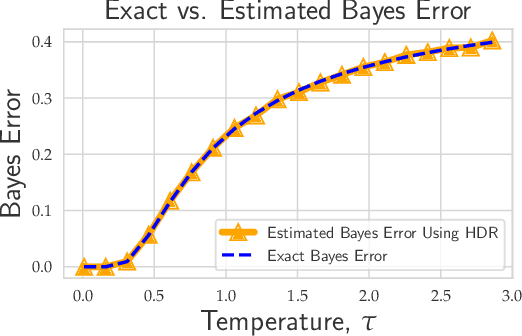
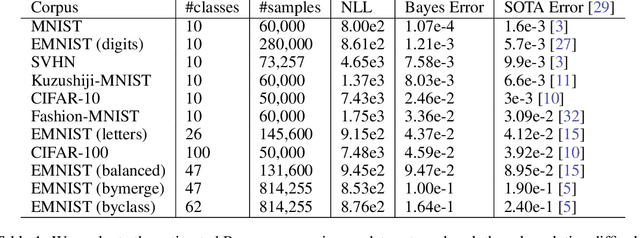
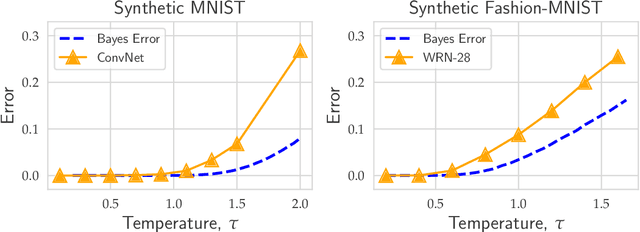
Evaluating the inherent difficulty of a given data-driven classification problem is important for establishing absolute benchmarks and evaluating progress in the field. To this end, a natural quantity to consider is the \emph{Bayes error}, which measures the optimal classification error theoretically achievable for a given data distribution. While generally an intractable quantity, we show that we can compute the exact Bayes error of generative models learned using normalizing flows. Our technique relies on a fundamental result, which states that the Bayes error is invariant under invertible transformation. Therefore, we can compute the exact Bayes error of the learned flow models by computing it for Gaussian base distributions, which can be done efficiently using Holmes-Diaconis-Ross integration. Moreover, we show that by varying the temperature of the learned flow models, we can generate synthetic datasets that closely resemble standard benchmark datasets, but with almost any desired Bayes error. We use our approach to conduct a thorough investigation of state-of-the-art classification models, and find that in some -- but not all -- cases, these models are capable of obtaining accuracy very near optimal. Finally, we use our method to evaluate the intrinsic "hardness" of standard benchmark datasets, and classes within those datasets.

Good linear classifiers are abundant in the interpolating regime

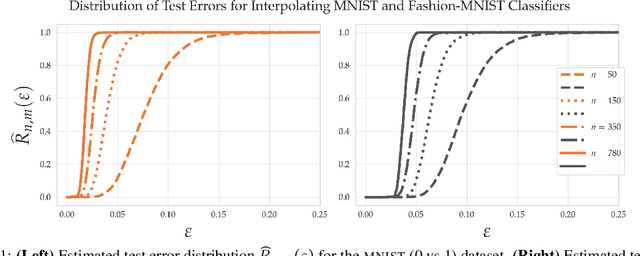
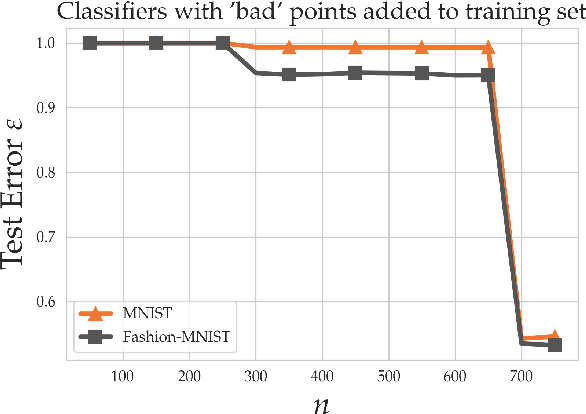
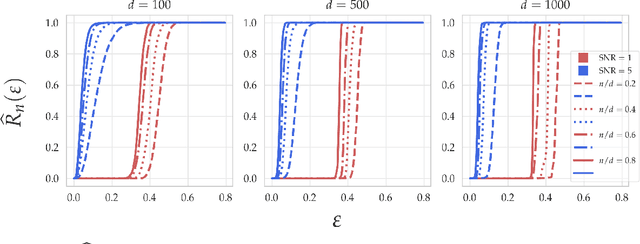
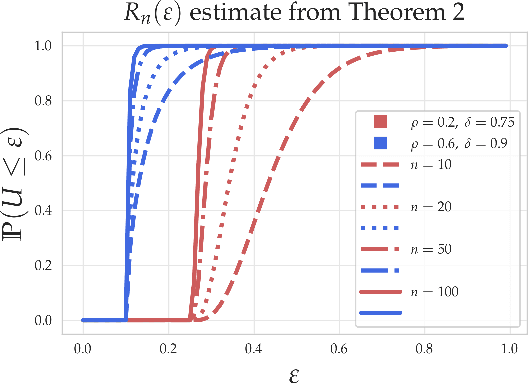
Within the machine learning community, the widely-used uniform convergence framework seeks to answer the question of how complex models such as modern neural networks can generalize well to new data. This approach bounds the test error of the \emph{worst-case} model one could have fit to the data, which presents fundamental limitations. In this paper, we revisit the statistical mechanics approach to learning, which instead attempts to understand the behavior of the \emph{typical} model. To quantify this typicality in the setting of over-parameterized linear classification, we develop a methodology to compute the full distribution of test errors among interpolating classifiers. We apply our method to compute this distribution for several real and synthetic datasets. We find that in many regimes of interest, an overwhelming proportion of interpolating classifiers have good test performance, even though---as we demonstrate---classifiers with very high test error do exist. This shows that the behavior of the worst-case model can deviate substantially from that of the usual model. Furthermore, we observe that for a given training set and testing distribution, there is a critical value $\varepsilon^* > 0$ which is \emph{typical}, in the sense that nearly all test errors eventually concentrate around it. Based on these empirical results, we study this phenomenon theoretically under simplifying assumptions on the data, and we derive simple asymptotic expressions for both the distribution of test errors as well as the critical value $\varepsilon^*$. Both of these results qualitatively reproduce our empirical findings. Our results show that the usual style of analysis in statistical learning theory may not be fine-grained enough to capture the good generalization performance observed in practice, and that approaches based on the statistical mechanics of learning offer a promising alternative.

Global Capacity Measures for Deep ReLU Networks via Path Sampling

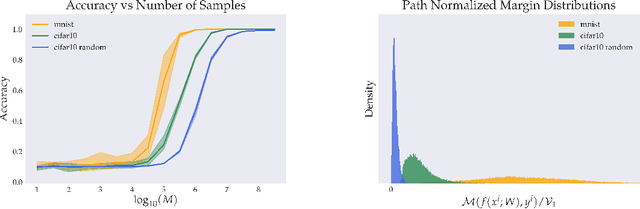
Classical results on the statistical complexity of linear models have commonly identified the norm of the weights $\|w\|$ as a fundamental capacity measure. Generalizations of this measure to the setting of deep networks have been varied, though a frequently identified quantity is the product of weight norms of each layer. In this work, we show that for a large class of networks possessing a positive homogeneity property, similar bounds may be obtained instead in terms of the norm of the product of weights. Our proof technique generalizes a recently proposed sampling argument, which allows us to demonstrate the existence of sparse approximants of positive homogeneous networks. This yields covering number bounds, which can be converted to generalization bounds for multi-class classification that are comparable to, and in certain cases improve upon, existing results in the literature. Finally, we investigate our sampling procedure empirically, which yields results consistent with our theory.