Neural Program Meta-Induction

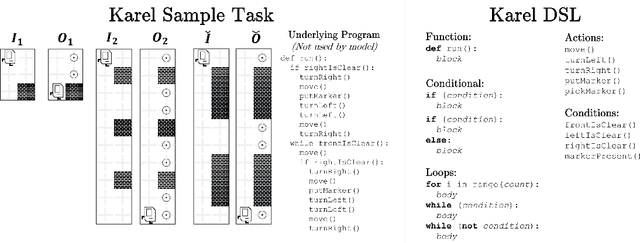
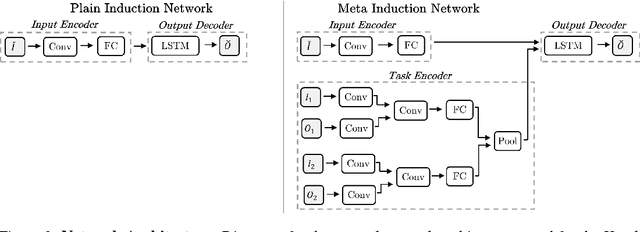
Most recently proposed methods for Neural Program Induction work under the assumption of having a large set of input/output (I/O) examples for learning any underlying input-output mapping. This paper aims to address the problem of data and computation efficiency of program induction by leveraging information from related tasks. Specifically, we propose two approaches for cross-task knowledge transfer to improve program induction in limited-data scenarios. In our first proposal, portfolio adaptation, a set of induction models is pretrained on a set of related tasks, and the best model is adapted towards the new task using transfer learning. In our second approach, meta program induction, a $k$-shot learning approach is used to make a model generalize to new tasks without additional training. To test the efficacy of our methods, we constructed a new benchmark of programs written in the Karel programming language. Using an extensive experimental evaluation on the Karel benchmark, we demonstrate that our proposals dramatically outperform the baseline induction method that does not use knowledge transfer. We also analyze the relative performance of the two approaches and study conditions in which they perform best. In particular, meta induction outperforms all existing approaches under extreme data sparsity (when a very small number of examples are available), i.e., fewer than ten. As the number of available I/O examples increase (i.e. a thousand or more), portfolio adapted program induction becomes the best approach. For intermediate data sizes, we demonstrate that the combined method of adapted meta program induction has the strongest performance.

Learning to superoptimize programs

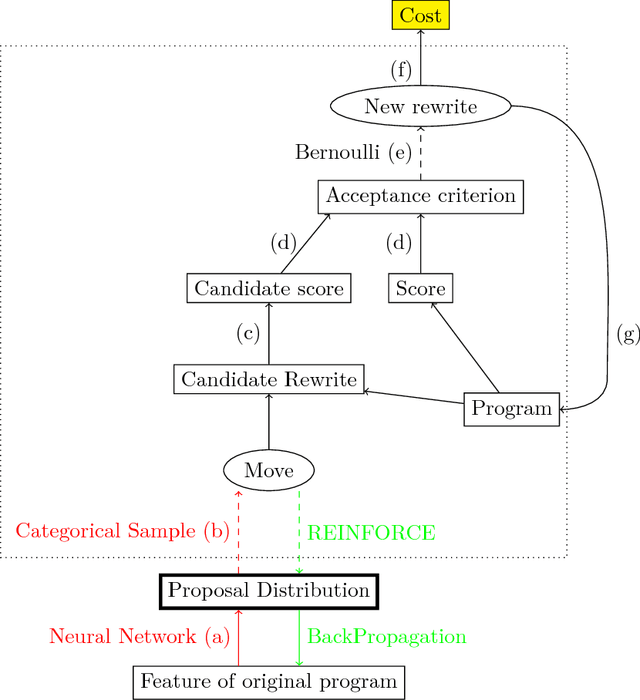
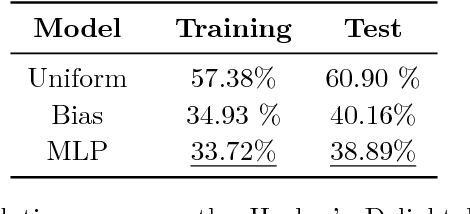
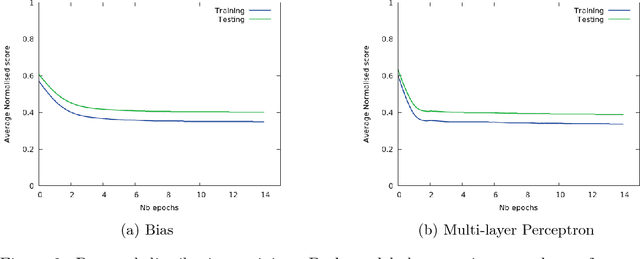
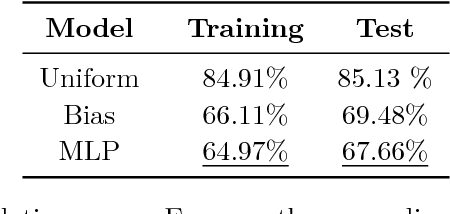
Code super-optimization is the task of transforming any given program to a more efficient version while preserving its input-output behaviour. In some sense, it is similar to the paraphrase problem from natural language processing where the intention is to change the syntax of an utterance without changing its semantics. Code-optimization has been the subject of years of research that has resulted in the development of rule-based transformation strategies that are used by compilers. More recently, however, a class of stochastic search based methods have been shown to outperform these strategies. This approach involves repeated sampling of modifications to the program from a proposal distribution, which are accepted or rejected based on whether they preserve correctness, and the improvement they achieve. These methods, however, neither learn from past behaviour nor do they try to leverage the semantics of the program under consideration. Motivated by this observation, we present a novel learning based approach for code super-optimization. Intuitively, our method works by learning the proposal distribution using unbiased estimators of the gradient of the expected improvement. Experiments on benchmarks comprising of automatically generated as well as existing ("Hacker's Delight") programs show that the proposed method is able to significantly outperform state of the art approaches for code super-optimization.

Efficient Linear Programming for Dense CRFs

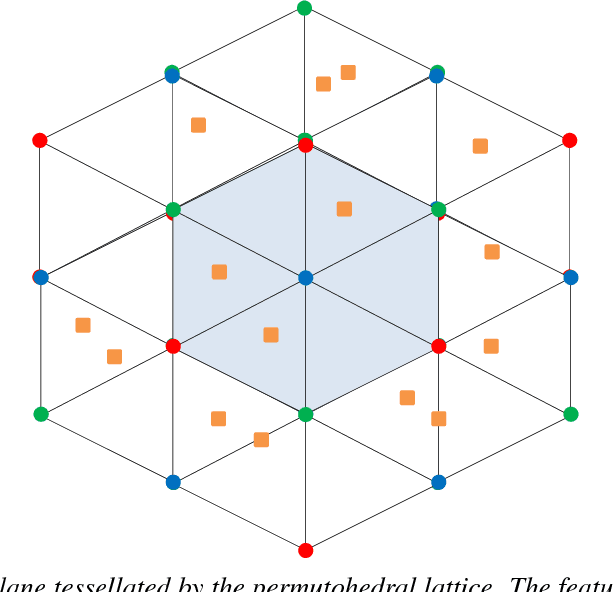
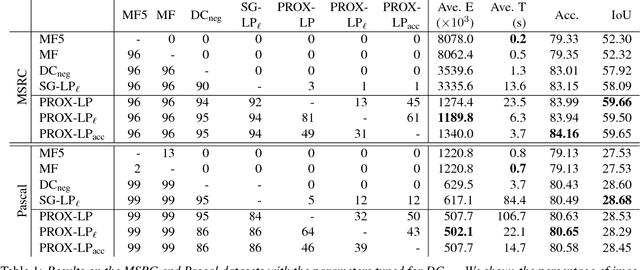
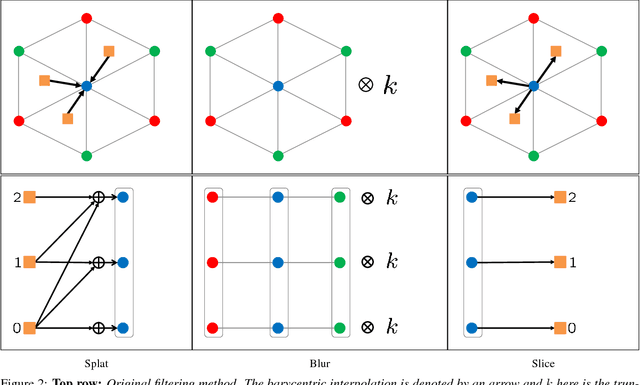
The fully connected conditional random field (CRF) with Gaussian pairwise potentials has proven popular and effective for multi-class semantic segmentation. While the energy of a dense CRF can be minimized accurately using a linear programming (LP) relaxation, the state-of-the-art algorithm is too slow to be useful in practice. To alleviate this deficiency, we introduce an efficient LP minimization algorithm for dense CRFs. To this end, we develop a proximal minimization framework, where the dual of each proximal problem is optimized via block coordinate descent. We show that each block of variables can be efficiently optimized. Specifically, for one block, the problem decomposes into significantly smaller subproblems, each of which is defined over a single pixel. For the other block, the problem is optimized via conditional gradient descent. This has two advantages: 1) the conditional gradient can be computed in a time linear in the number of pixels and labels; and 2) the optimal step size can be computed analytically. Our experiments on standard datasets provide compelling evidence that our approach outperforms all existing baselines including the previous LP based approach for dense CRFs.

Learning to superoptimize programs - Workshop Version

Superoptimization requires the estimation of the best program for a given computational task. In order to deal with large programs, superoptimization techniques perform a stochastic search. This involves proposing a modification of the current program, which is accepted or rejected based on the improvement achieved. The state of the art method uses uniform proposal distributions, which fails to exploit the problem structure to the fullest. To alleviate this deficiency, we learn a proposal distribution over possible modifications using Reinforcement Learning. We provide convincing results on the superoptimization of "Hacker's Delight" programs.

Efficient Continuous Relaxations for Dense CRF

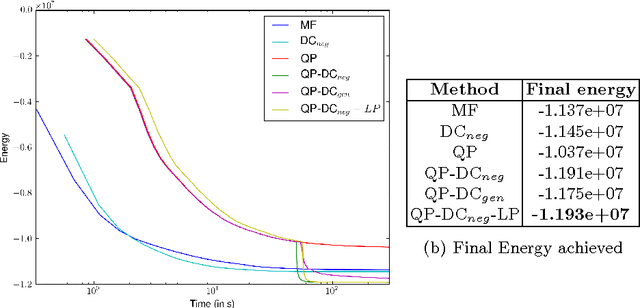
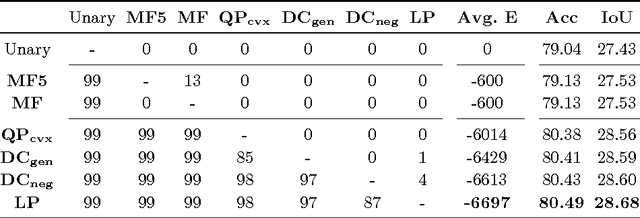
Dense conditional random fields (CRF) with Gaussian pairwise potentials have emerged as a popular framework for several computer vision applications such as stereo correspondence and semantic segmentation. By modeling long-range interactions, dense CRFs provide a more detailed labelling compared to their sparse counterparts. Variational inference in these dense models is performed using a filtering-based mean-field algorithm in order to obtain a fully-factorized distribution minimising the Kullback-Leibler divergence to the true distribution. In contrast to the continuous relaxation-based energy minimisation algorithms used for sparse CRFs, the mean-field algorithm fails to provide strong theoretical guarantees on the quality of its solutions. To address this deficiency, we show that it is possible to use the same filtering approach to speed-up the optimisation of several continuous relaxations. Specifically, we solve a convex quadratic programming (QP) relaxation using the efficient Frank-Wolfe algorithm. This also allows us to solve difference-of-convex relaxations via the iterative concave-convex procedure where each iteration requires solving a convex QP. Finally, we develop a novel divide-and-conquer method to compute the subgradients of a linear programming relaxation that provides the best theoretical bounds for energy minimisation. We demonstrate the advantage of continuous relaxations over the widely used mean-field algorithm on publicly available datasets.

Adaptive Neural Compilation

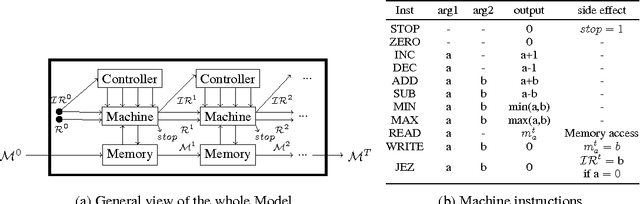
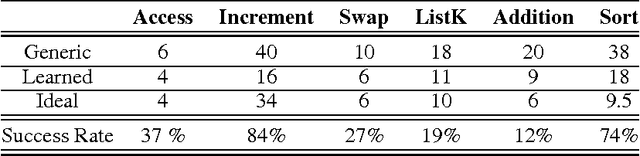
This paper proposes an adaptive neural-compilation framework to address the problem of efficient program learning. Traditional code optimisation strategies used in compilers are based on applying pre-specified set of transformations that make the code faster to execute without changing its semantics. In contrast, our work involves adapting programs to make them more efficient while considering correctness only on a target input distribution. Our approach is inspired by the recent works on differentiable representations of programs. We show that it is possible to compile programs written in a low-level language to a differentiable representation. We also show how programs in this representation can be optimised to make them efficient on a target distribution of inputs. Experimental results demonstrate that our approach enables learning specifically-tuned algorithms for given data distributions with a high success rate.