New Properties and Invariants of Harmonic Polygons

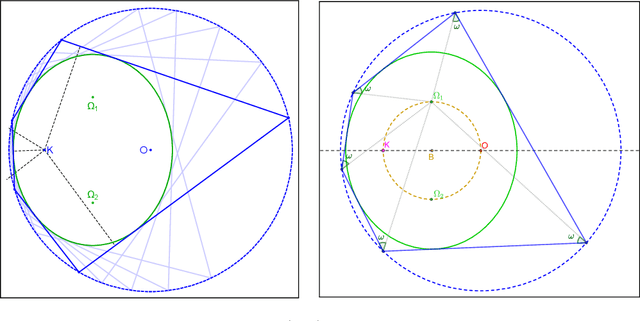
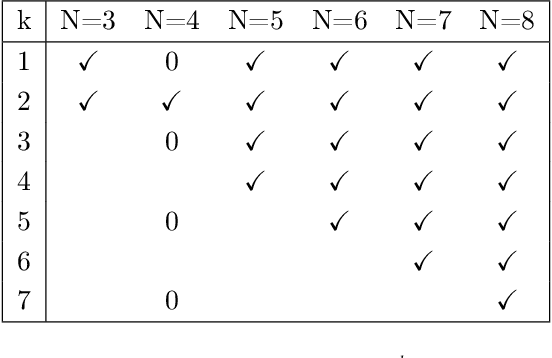
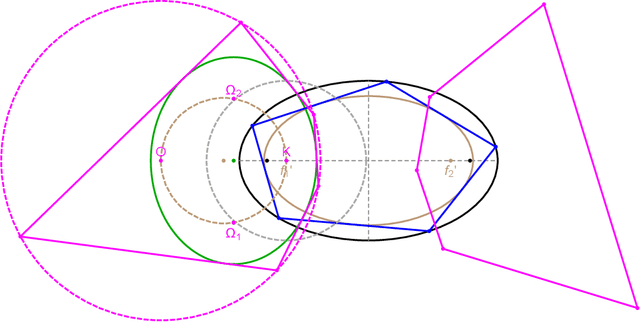
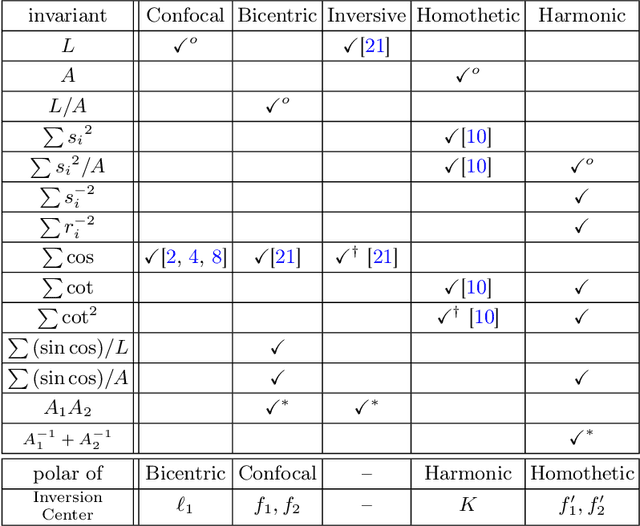
Via simulation, we discover and prove curious new Euclidean properties and invariants of the Poncelet family of harmonic polygons.

Properties of Parabola-Inscribed Poncelet Polygons

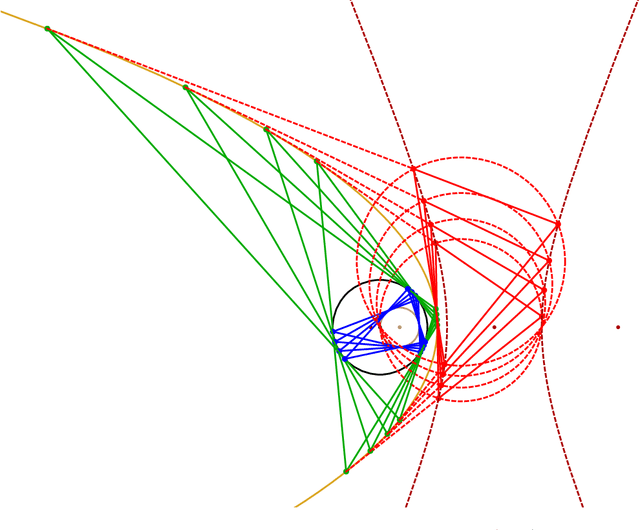
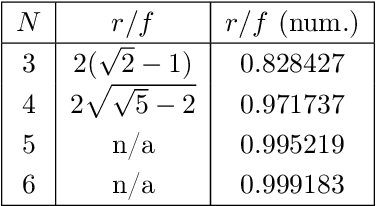
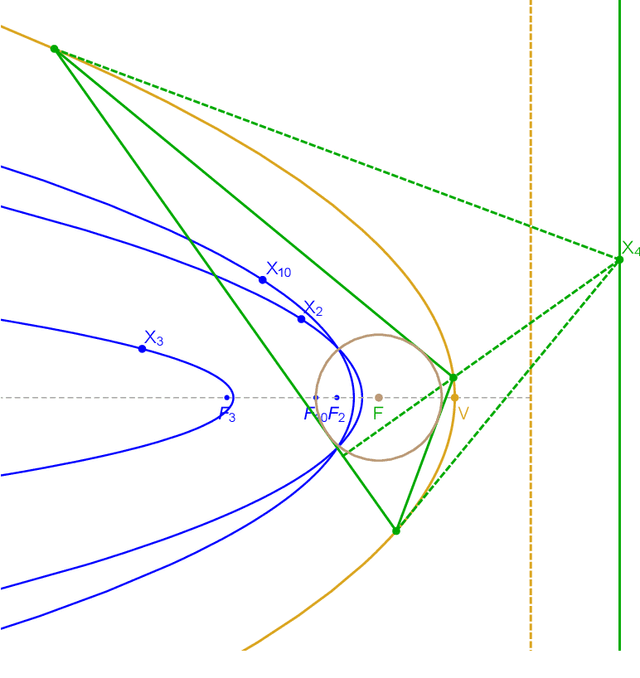
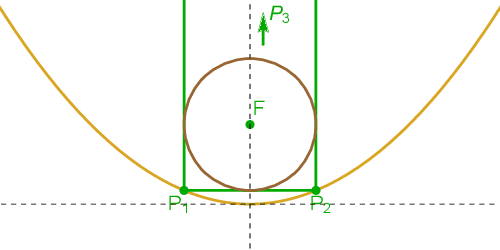
We investigate properties of Poncelet $N$-gon families inscribed in a parabola and circumscribing a focus-centered circle. These can be regarded as the polar images of a bicentric family with respect to the circumcircle, such that the bicentric incircle contains the circumcenter. We derive closure conditions for several $N$ and describe curious Euclidean properties such as straight line, circular, and point, loci, as well as a (perhaps new) conserved quantity.

Loci of Poncelet Triangles with Multiple Caustics

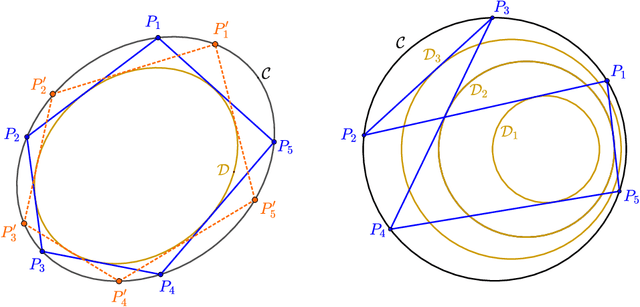
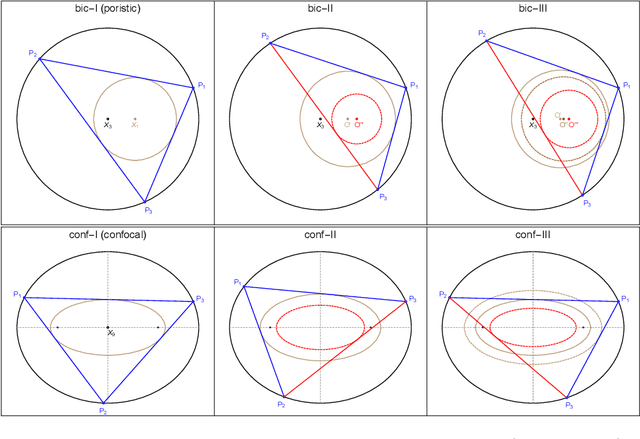
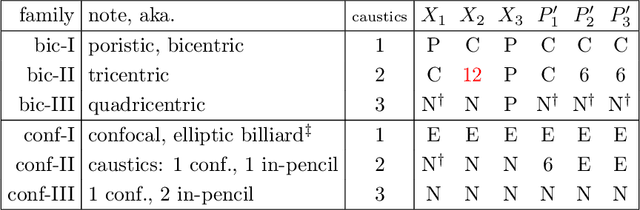
We analyze loci of triangles centers over variants of two-well known triangle porisms: the bicentric family and the confocal family. Specifically, we evoke a more general version of Poncelet's closure theorem whereby individual sides can be made tangent to separate caustics. We show that despite a more complicated dynamic geometry, the locus of certain triangle centers and associated points remain conics and/or circles.

A Theory for Locus Ellipticity of Poncelet 3-Periodic Centers

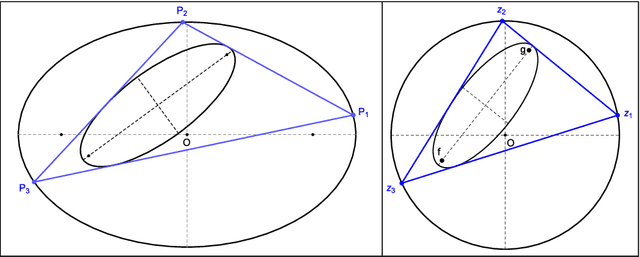
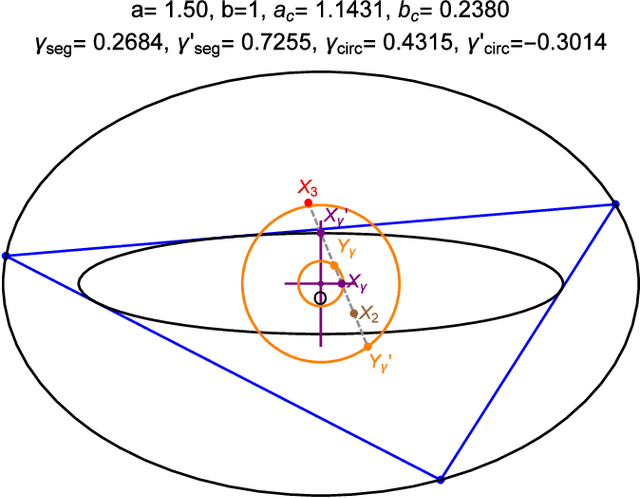
We propose a theory which predicts the ellipticity of a triangle center's locus over a Poncelet 3-periodic family. We show that if the triangle center can be expressed as a fixed affine combination of barycenter, circumcenter, and a third, stationary point over some family, then its locus will be an ellipse. Taking billiard 3-periodics as an example, the third point is the mittenpunkt. We derive conditions under which a locus degenerates to a segment or is a circle. We show a locus turning number is either plus or minus 3 and predict its movement monotonicity with respect to vertices of the 3-periodic family. Finally, we derive a (long) expression for the loci of the incenter and excenters over a generic Poncelet 3-periodic family, showing they are roots of a quartic. We conjecture (i) those loci are convex, and (ii) that they can only be ellipses if the pair is confocal, i.e., within a 1d subspace of the 5d space of ellipse pairs which admit 3-periodics.

Poncelet Plectra: Harmonious Properties of Cosine Space

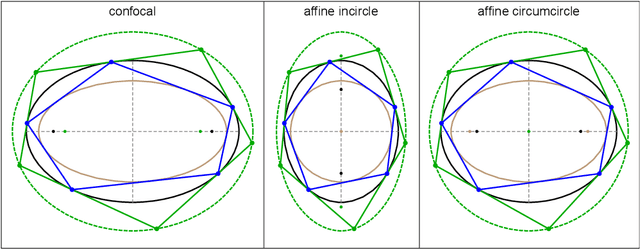
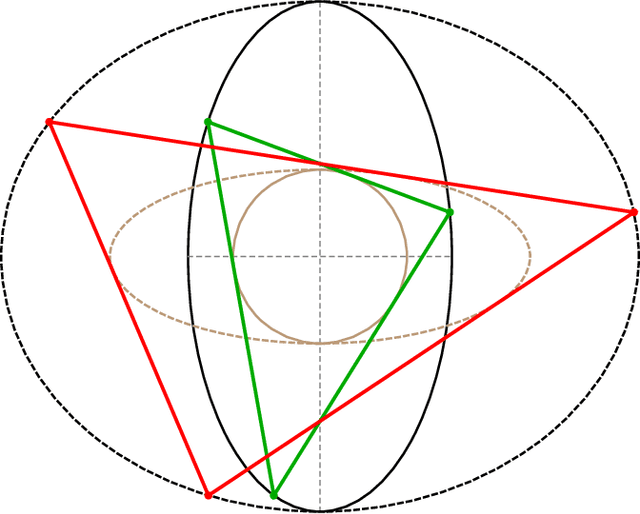
Poncelet N-periodics in a confocal pair (elliptic billiard) conserve the same sum of cosines as their affine image with fixed incircle. For N=3, the vector of cosines in either family sweep the same planar curve: an equilateral cubic resembling a plectrum (guitar pick). We also show that the family of excentral triangles to the confocal family conserves the same product of cosines as its affine image with fixed circumcircle. In cosine space cosine triples in either family sweep the same spherical curve. The associated planar curve in log cosine space is also plectrum-shaped, though rounder than the one swept by its parent confocal family.

Invariant Center Power and Elliptic Loci of Poncelet Triangles

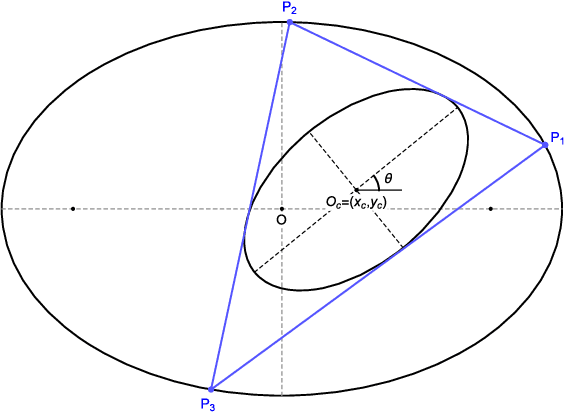
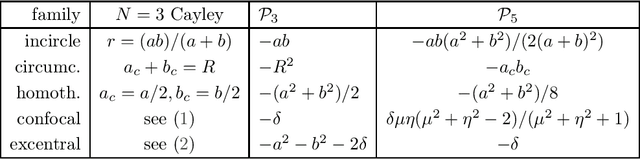
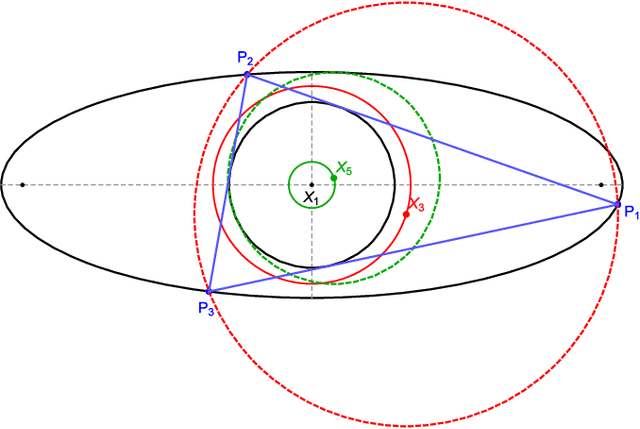
We study center power with respect to circles derived from Poncelet 3-periodics (triangles) in a generic pair of ellipses as well as loci of their triangle centers. We show that (i) for any concentric pair, the power of the center with respect to either circumcircle or Euler's circle is invariant, and (ii) if a triangle center of a 3-periodic in a generic nested pair is a fixed linear combination of barycenter and circumcenter, its locus over the family is an ellipse.

Family Ties: Relating Poncelet 3-Periodics by their Properties

We study the dynamic geometry, loci, and invariants of three Poncelet families associated with three distinct concentric Ellipse pairs: with-incircle, with-circumcircle, and homothetic. Most of their properties run parallel to those of 3 well-studied families: elliptic billiard (confocal pair), Chapple's poristic triangles, and the Brocard porism, allowing us to organize them in three "similar" groups.

Invariants of Self-Intersected N-Periodics in the Elliptic Billiard

We study self-intersected N-periodics in the elliptic billiard, describing new facts about their geometry (e.g., self-intersected 4-periodics have vertices concyclic with the foci). We also check if some invariants listed in "Eighty New Invariants of N-Periodics in the Elliptic Billiard" (2020), arXiv:2004.12497, remain invariant in the self-intersected case. Toward that end, we derive explicit expressions for many low-N simple and self-intersected cases. We identify two special cases (one simple, one self-intersected) where a quantity prescribed to be invariant is actually variable.

Loci and Envelopes of Ellipse-Inscribed Triangles

We study a family of ellipse-inscribed triangles with two vertices V1,V2 fixed on the ellipse boundary while a third one which sweeps it. We prove that: (i) if a triangle center is a fixed linear combination of barycenter and orthocenter, its locus over the family is an ellipse; (ii) over the 1d family of said linear combinations, loci centers sweep a line; (iii) over the family of parallel V1V2, said elliptic loci are rigidly-translating ellipses. Additionally, we study the external envelope of elliptic loci for fixed V1 and over all V2 on the ellipse. We show that (iv) the area of said envelope is invariant with respect to V1, and that (v) for the barycenter (resp. orthocenter), the envelope is an ellipse (resp. an affine image of Pascal's Lima\c{c}on).

An Infinite, Converging, Sequence of Brocard Porisms

The Brocard porism is a known 1d family of triangles inscribed in a circle and circumscribed about an ellipse. Remarkably, the Brocard angle is invariant and the Brocard points are stationary at the foci of the ellipse. In this paper we show that a certain derived triangle spawns off a second, smaller, Brocard porism so that repeating this calculation produces an infinite, converging sequence of porisms. We also show that this sequence is embedded in a continuous family of porisms.