Poncelet Plectra: Harmonious Properties of Cosine Space

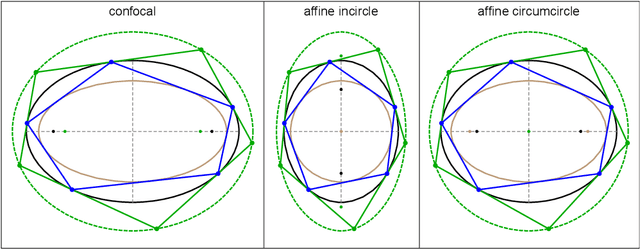
Poncelet N-periodics in a confocal pair (elliptic billiard) conserve the same sum of cosines as their affine image with fixed incircle. For N=3, the vector of cosines in either family sweep the same planar curve: an equilateral cubic resembling a plectrum (guitar pick). We also show that the family of excentral triangles to the confocal family conserves the same product of cosines as its affine image with fixed circumcircle. In cosine space cosine triples in either family sweep the same spherical curve. The associated planar curve in log cosine space is also plectrum-shaped, though rounder than the one swept by its parent confocal family.

Poncelet Propellers: Invariant Total Blade Area

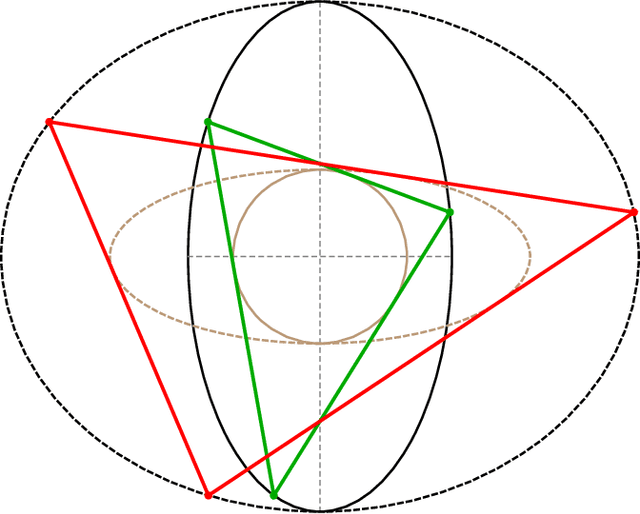
Given a triangle, a trio of circumellipses can be defined, each centered on an excenter. Over the family of Poncelet 3-periodics (triangles) in a concentric ellipse pair (axis-aligned or not), the trio resembles a rotating propeller, where each "blade" has variable area. Amazingly, their total area is invariant, even when the ellipse pair is not axis-aligned. We also prove a closely-related invariant involving the sum of blade-to-excircle area ratios.