A Theory for Locus Ellipticity of Poncelet 3-Periodic Centers

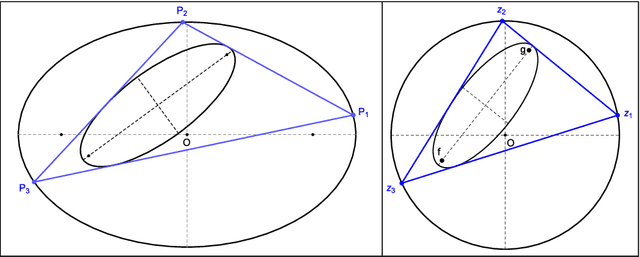
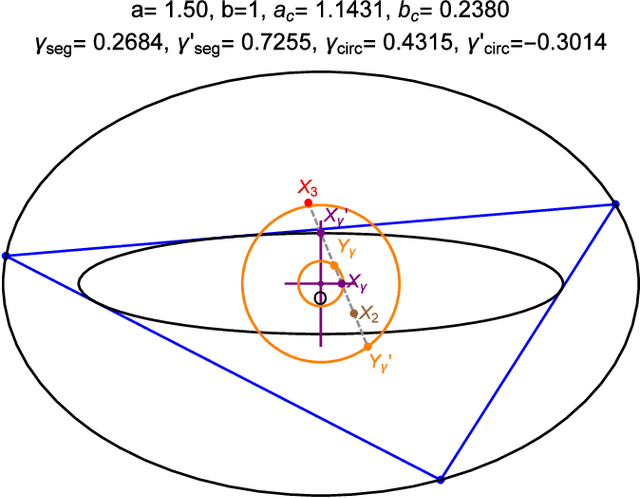
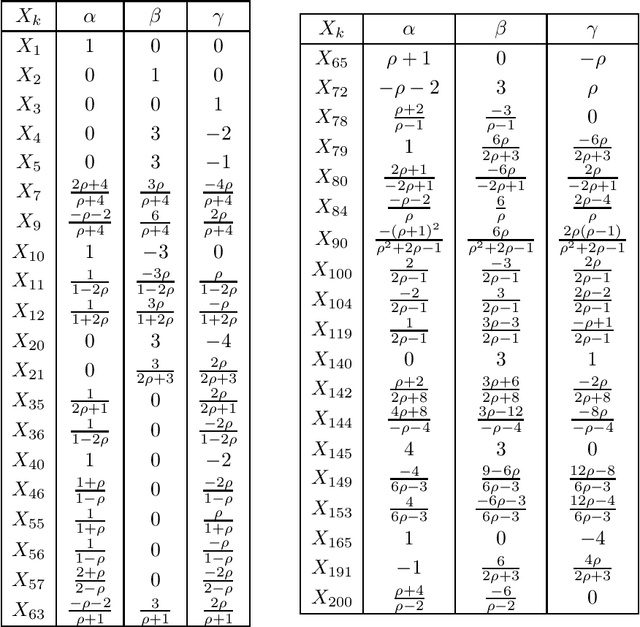
We propose a theory which predicts the ellipticity of a triangle center's locus over a Poncelet 3-periodic family. We show that if the triangle center can be expressed as a fixed affine combination of barycenter, circumcenter, and a third, stationary point over some family, then its locus will be an ellipse. Taking billiard 3-periodics as an example, the third point is the mittenpunkt. We derive conditions under which a locus degenerates to a segment or is a circle. We show a locus turning number is either plus or minus 3 and predict its movement monotonicity with respect to vertices of the 3-periodic family. Finally, we derive a (long) expression for the loci of the incenter and excenters over a generic Poncelet 3-periodic family, showing they are roots of a quartic. We conjecture (i) those loci are convex, and (ii) that they can only be ellipses if the pair is confocal, i.e., within a 1d subspace of the 5d space of ellipse pairs which admit 3-periodics.

Invariant Center Power and Elliptic Loci of Poncelet Triangles

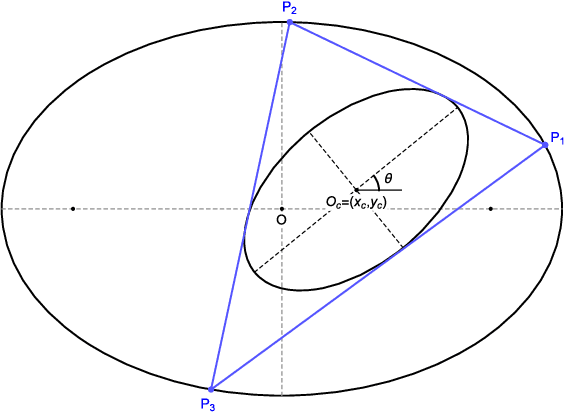
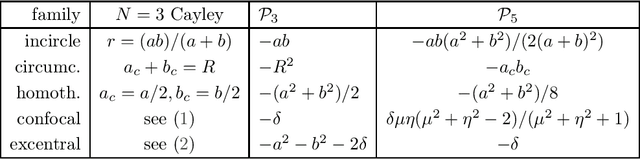
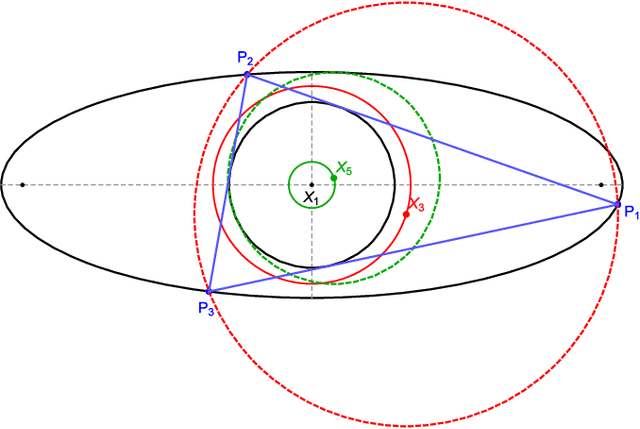
We study center power with respect to circles derived from Poncelet 3-periodics (triangles) in a generic pair of ellipses as well as loci of their triangle centers. We show that (i) for any concentric pair, the power of the center with respect to either circumcircle or Euler's circle is invariant, and (ii) if a triangle center of a 3-periodic in a generic nested pair is a fixed linear combination of barycenter and circumcenter, its locus over the family is an ellipse.

Poncelet Propellers: Invariant Total Blade Area

Given a triangle, a trio of circumellipses can be defined, each centered on an excenter. Over the family of Poncelet 3-periodics (triangles) in a concentric ellipse pair (axis-aligned or not), the trio resembles a rotating propeller, where each "blade" has variable area. Amazingly, their total area is invariant, even when the ellipse pair is not axis-aligned. We also prove a closely-related invariant involving the sum of blade-to-excircle area ratios.