Efficient hyperparameter optimization by way of PAC-Bayes bound minimization

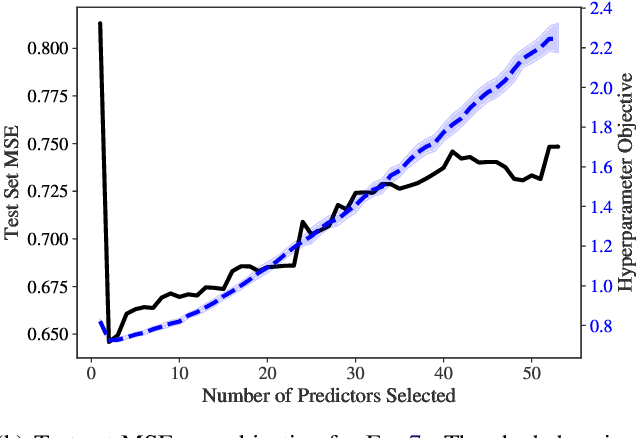
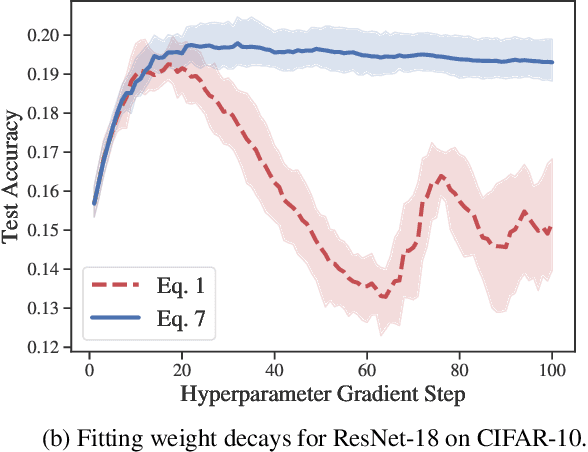
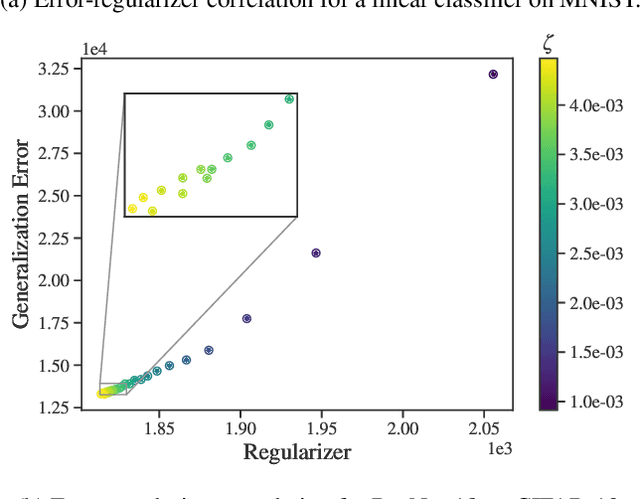
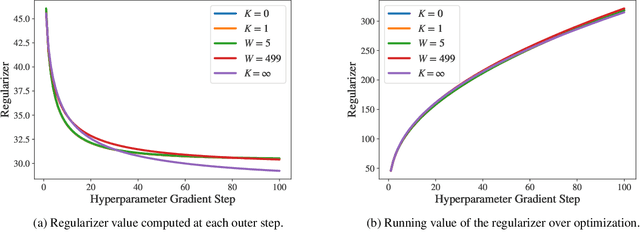
Identifying optimal values for a high-dimensional set of hyperparameters is a problem that has received growing attention given its importance to large-scale machine learning applications such as neural architecture search. Recently developed optimization methods can be used to select thousands or even millions of hyperparameters. Such methods often yield overfit models, however, leading to poor performance on unseen data. We argue that this overfitting results from using the standard hyperparameter optimization objective function. Here we present an alternative objective that is equivalent to a Probably Approximately Correct-Bayes (PAC-Bayes) bound on the expected out-of-sample error. We then devise an efficient gradient-based algorithm to minimize this objective; the proposed method has asymptotic space and time complexity equal to or better than other gradient-based hyperparameter optimization methods. We show that this new method significantly reduces out-of-sample error when applied to hyperparameter optimization problems known to be prone to overfitting.

Theano: A Python framework for fast computation of mathematical expressions

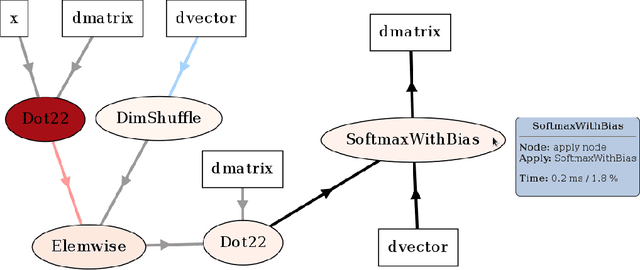
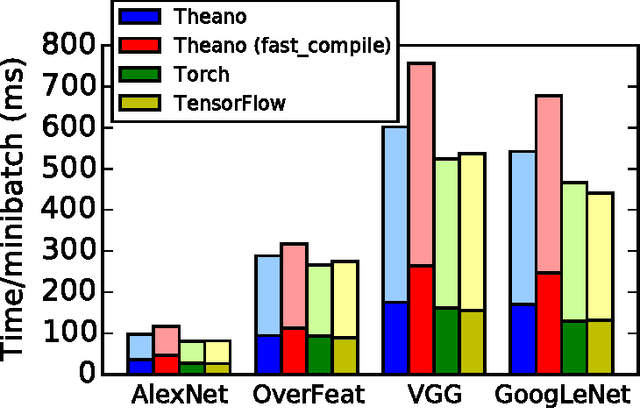
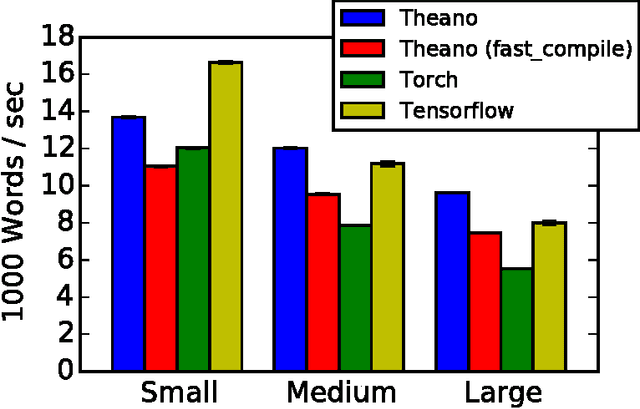
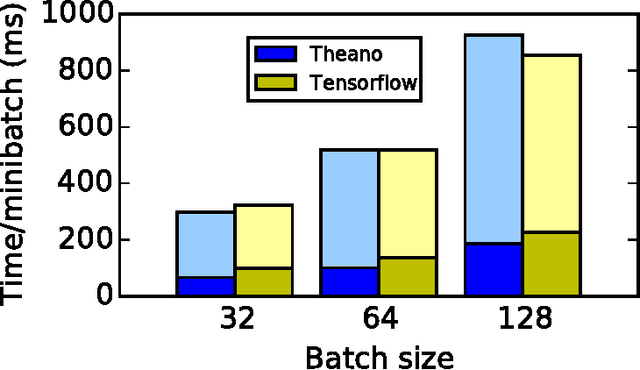
Theano is a Python library that allows to define, optimize, and evaluate mathematical expressions involving multi-dimensional arrays efficiently. Since its introduction, it has been one of the most used CPU and GPU mathematical compilers - especially in the machine learning community - and has shown steady performance improvements. Theano is being actively and continuously developed since 2008, multiple frameworks have been built on top of it and it has been used to produce many state-of-the-art machine learning models. The present article is structured as follows. Section I provides an overview of the Theano software and its community. Section II presents the principal features of Theano and how to use them, and compares them with other similar projects. Section III focuses on recently-introduced functionalities and improvements. Section IV compares the performance of Theano against Torch7 and TensorFlow on several machine learning models. Section V discusses current limitations of Theano and potential ways of improving it.

Understanding Protein Dynamics with L1-Regularized Reversible Hidden Markov Models

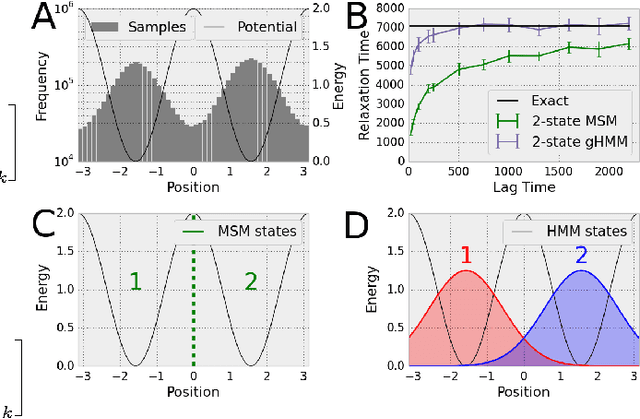
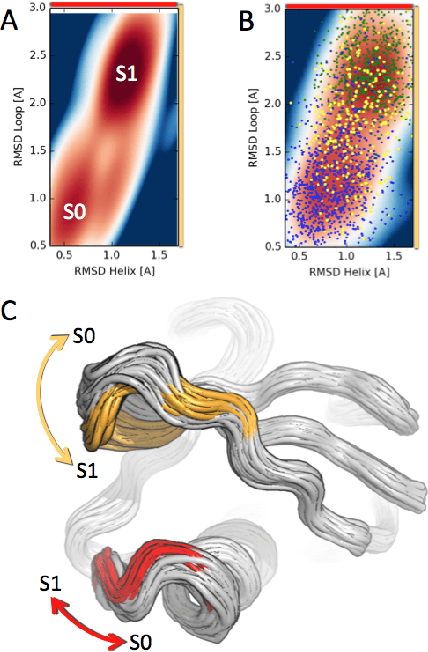
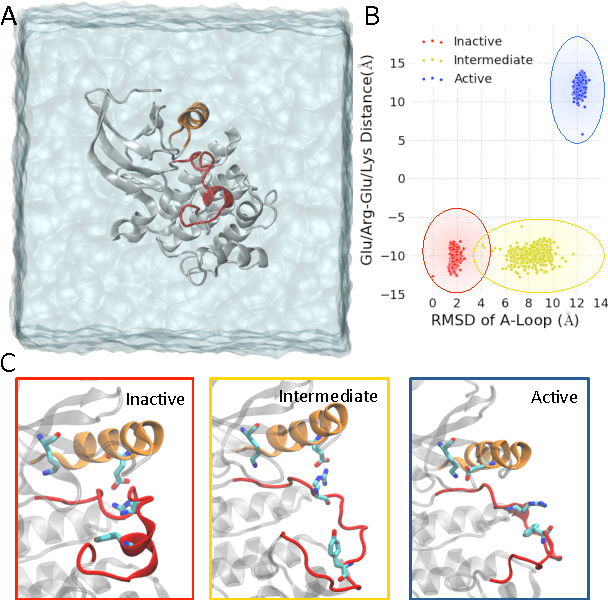
We present a machine learning framework for modeling protein dynamics. Our approach uses L1-regularized, reversible hidden Markov models to understand large protein datasets generated via molecular dynamics simulations. Our model is motivated by three design principles: (1) the requirement of massive scalability; (2) the need to adhere to relevant physical law; and (3) the necessity of providing accessible interpretations, critical for both cellular biology and rational drug design. We present an EM algorithm for learning and introduce a model selection criteria based on the physical notion of convergence in relaxation timescales. We contrast our model with standard methods in biophysics and demonstrate improved robustness. We implement our algorithm on GPUs and apply the method to two large protein simulation datasets generated respectively on the NCSA Bluewaters supercomputer and the Folding@Home distributed computing network. Our analysis identifies the conformational dynamics of the ubiquitin protein critical to cellular signaling, and elucidates the stepwise activation mechanism of the c-Src kinase protein.