Data-Mining Textual Responses to Uncover Misconception Patterns

An important, yet largely unstudied, problem in student data analysis is to detect misconceptions from students' responses to open-response questions. Misconception detection enables instructors to deliver more targeted feedback on the misconceptions exhibited by many students in their class, thus improving the quality of instruction. In this paper, we propose a new natural language processing-based framework to detect the common misconceptions among students' textual responses to short-answer questions. We propose a probabilistic model for students' textual responses involving misconceptions and experimentally validate it on a real-world student-response dataset. Experimental results show that our proposed framework excels at classifying whether a response exhibits one or more misconceptions. More importantly, it can also automatically detect the common misconceptions exhibited across responses from multiple students to multiple questions; this property is especially important at large scale, since instructors will no longer need to manually specify all possible misconceptions that students might exhibit.

Learning to Invert: Signal Recovery via Deep Convolutional Networks

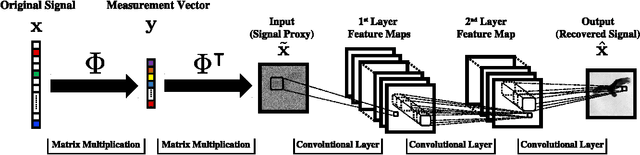
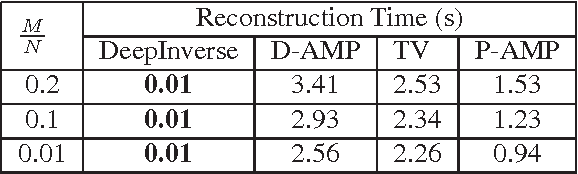
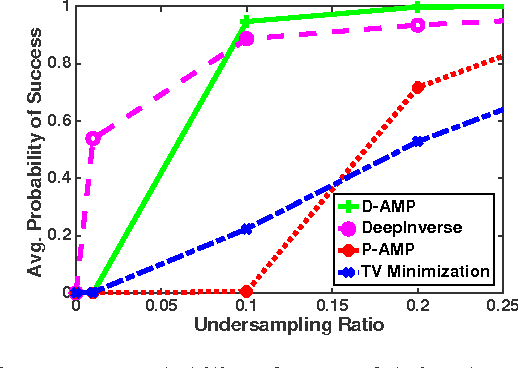
The promise of compressive sensing (CS) has been offset by two significant challenges. First, real-world data is not exactly sparse in a fixed basis. Second, current high-performance recovery algorithms are slow to converge, which limits CS to either non-real-time applications or scenarios where massive back-end computing is available. In this paper, we attack both of these challenges head-on by developing a new signal recovery framework we call {\em DeepInverse} that learns the inverse transformation from measurement vectors to signals using a {\em deep convolutional network}. When trained on a set of representative images, the network learns both a representation for the signals (addressing challenge one) and an inverse map approximating a greedy or convex recovery algorithm (addressing challenge two). Our experiments indicate that the DeepInverse network closely approximates the solution produced by state-of-the-art CS recovery algorithms yet is hundreds of times faster in run time. The tradeoff for the ultrafast run time is a computationally intensive, off-line training procedure typical to deep networks. However, the training needs to be completed only once, which makes the approach attractive for a host of sparse recovery problems.

Semi-Supervised Learning with the Deep Rendering Mixture Model

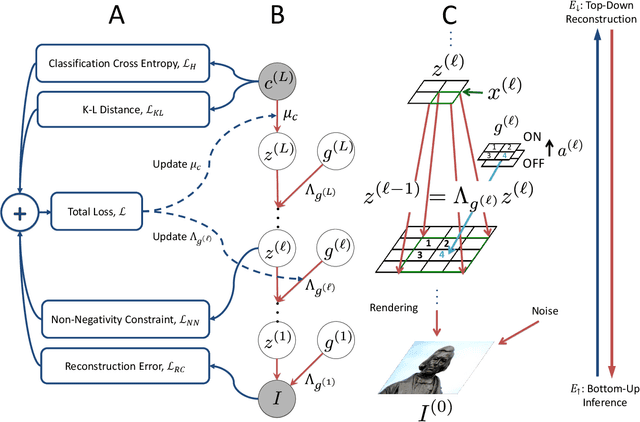
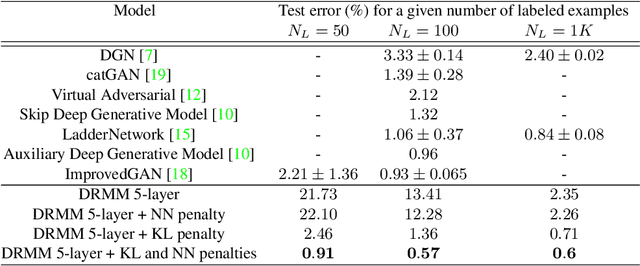
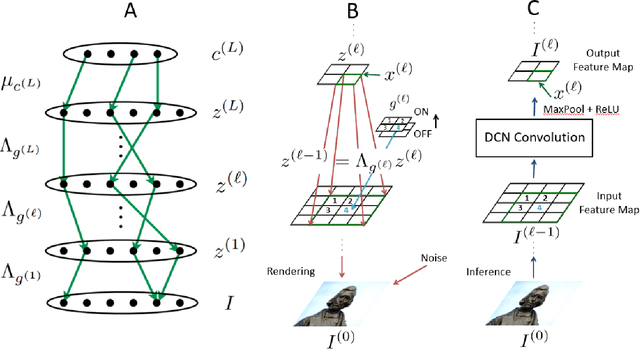
Semi-supervised learning algorithms reduce the high cost of acquiring labeled training data by using both labeled and unlabeled data during learning. Deep Convolutional Networks (DCNs) have achieved great success in supervised tasks and as such have been widely employed in the semi-supervised learning. In this paper we leverage the recently developed Deep Rendering Mixture Model (DRMM), a probabilistic generative model that models latent nuisance variation, and whose inference algorithm yields DCNs. We develop an EM algorithm for the DRMM to learn from both labeled and unlabeled data. Guided by the theory of the DRMM, we introduce a novel non-negativity constraint and a variational inference term. We report state-of-the-art performance on MNIST and SVHN and competitive results on CIFAR10. We also probe deeper into how a DRMM trained in a semi-supervised setting represents latent nuisance variation using synthetically rendered images. Taken together, our work provides a unified framework for supervised, unsupervised, and semi-supervised learning.

A Probabilistic Framework for Deep Learning

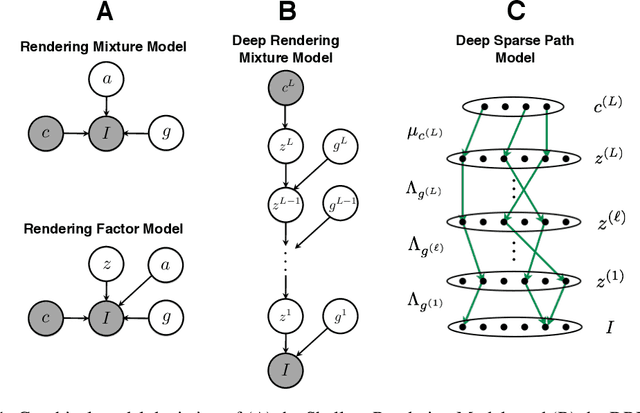
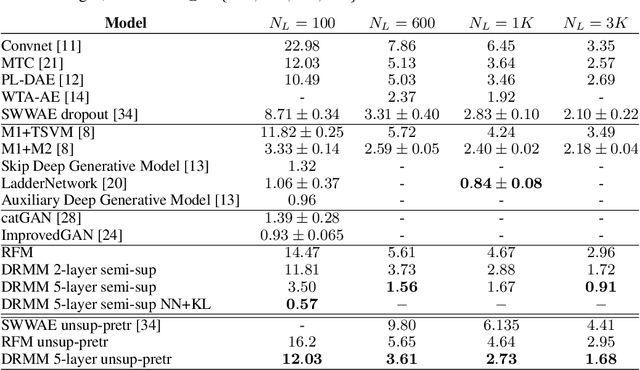
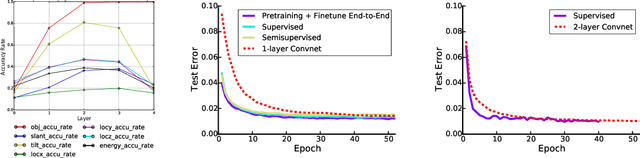
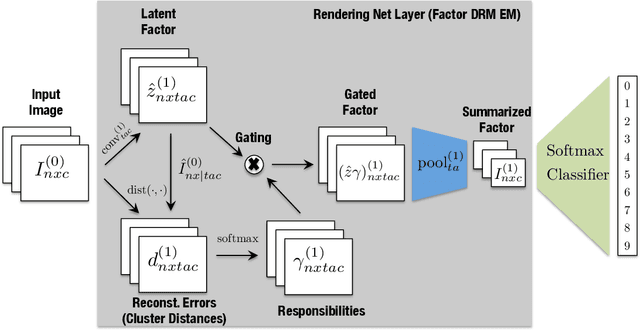
We develop a probabilistic framework for deep learning based on the Deep Rendering Mixture Model (DRMM), a new generative probabilistic model that explicitly capture variations in data due to latent task nuisance variables. We demonstrate that max-sum inference in the DRMM yields an algorithm that exactly reproduces the operations in deep convolutional neural networks (DCNs), providing a first principles derivation. Our framework provides new insights into the successes and shortcomings of DCNs as well as a principled route to their improvement. DRMM training via the Expectation-Maximization (EM) algorithm is a powerful alternative to DCN back-propagation, and initial training results are promising. Classification based on the DRMM and other variants outperforms DCNs in supervised digit classification, training 2-3x faster while achieving similar accuracy. Moreover, the DRMM is applicable to semi-supervised and unsupervised learning tasks, achieving results that are state-of-the-art in several categories on the MNIST benchmark and comparable to state of the art on the CIFAR10 benchmark.

RankMap: A Platform-Aware Framework for Distributed Learning from Dense Datasets

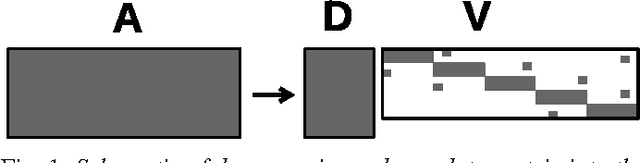
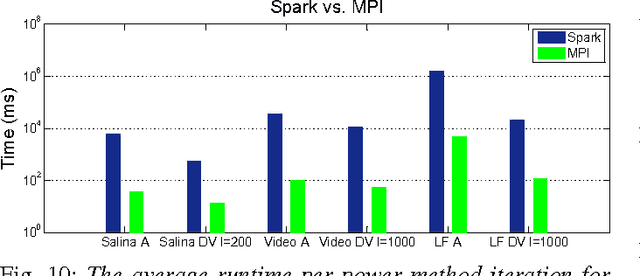
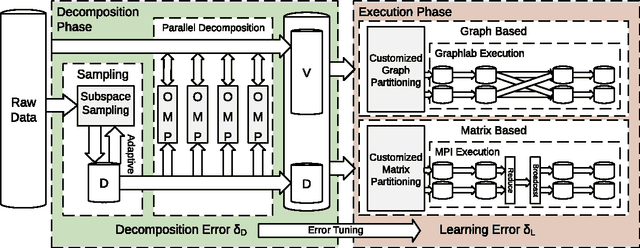
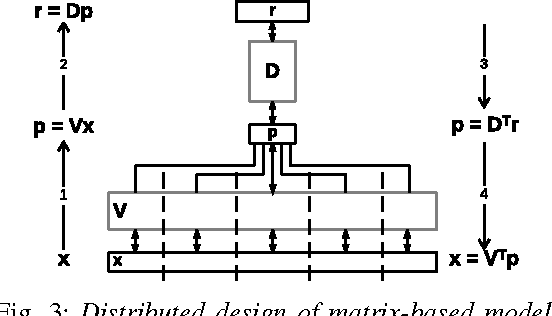
This paper introduces RankMap, a platform-aware end-to-end framework for efficient execution of a broad class of iterative learning algorithms for massive and dense datasets. Our framework exploits data structure to factorize it into an ensemble of lower rank subspaces. The factorization creates sparse low-dimensional representations of the data, a property which is leveraged to devise effective mapping and scheduling of iterative learning algorithms on the distributed computing machines. We provide two APIs, one matrix-based and one graph-based, which facilitate automated adoption of the framework for performing several contemporary learning applications. To demonstrate the utility of RankMap, we solve sparse recovery and power iteration problems on various real-world datasets with up to 1.8 billion non-zeros. Our evaluations are performed on Amazon EC2 and IBM iDataPlex servers using up to 244 cores. The results demonstrate up to two orders of magnitude improvements in memory usage, execution speed, and bandwidth compared with the best reported prior work, while achieving the same level of learning accuracy.

From Denoising to Compressed Sensing

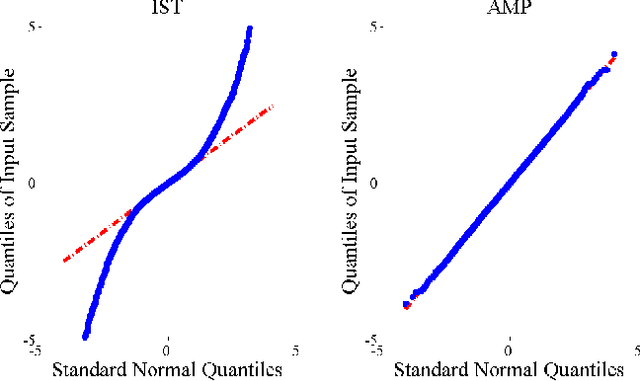
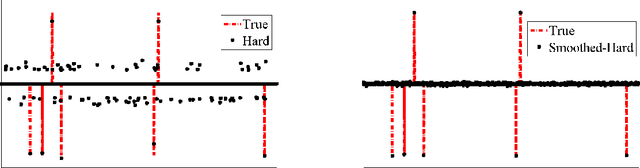
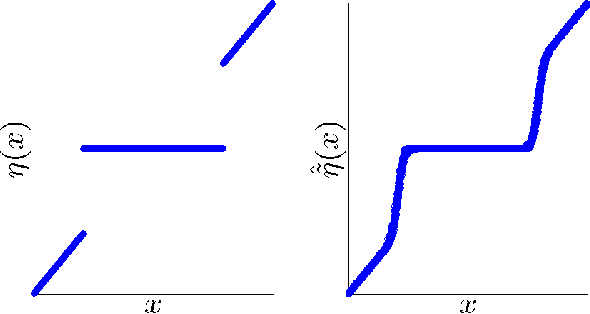
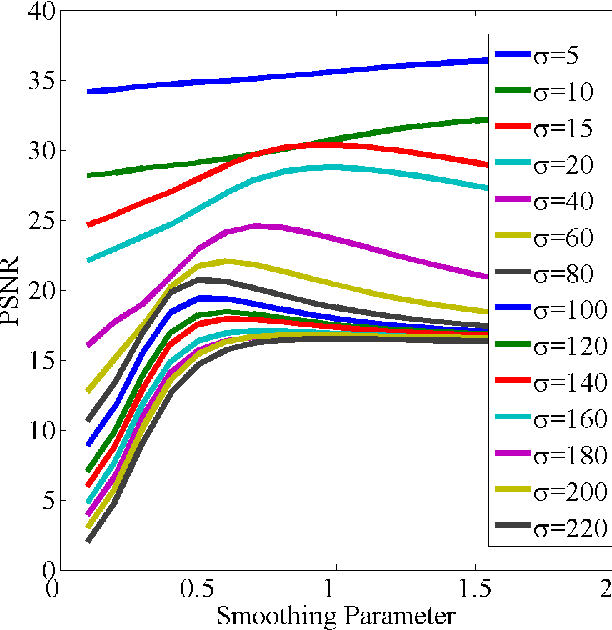
A denoising algorithm seeks to remove noise, errors, or perturbations from a signal. Extensive research has been devoted to this arena over the last several decades, and as a result, today's denoisers can effectively remove large amounts of additive white Gaussian noise. A compressed sensing (CS) reconstruction algorithm seeks to recover a structured signal acquired using a small number of randomized measurements. Typical CS reconstruction algorithms can be cast as iteratively estimating a signal from a perturbed observation. This paper answers a natural question: How can one effectively employ a generic denoiser in a CS reconstruction algorithm? In response, we develop an extension of the approximate message passing (AMP) framework, called Denoising-based AMP (D-AMP), that can integrate a wide class of denoisers within its iterations. We demonstrate that, when used with a high performance denoiser for natural images, D-AMP offers state-of-the-art CS recovery performance while operating tens of times faster than competing methods. We explain the exceptional performance of D-AMP by analyzing some of its theoretical features. A key element in D-AMP is the use of an appropriate Onsager correction term in its iterations, which coerces the signal perturbation at each iteration to be very close to the white Gaussian noise that denoisers are typically designed to remove.

Convex Biclustering

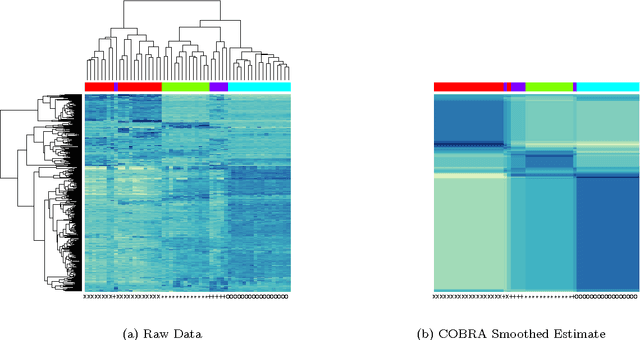
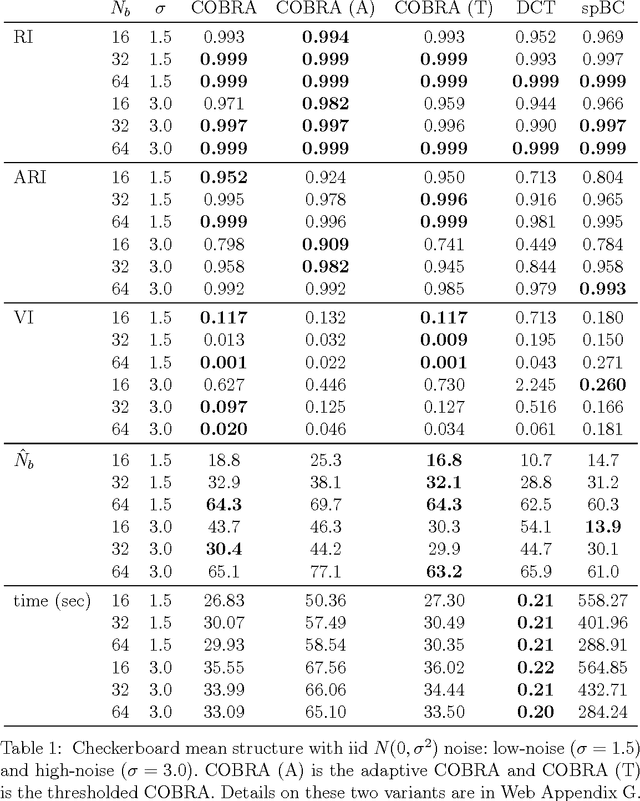
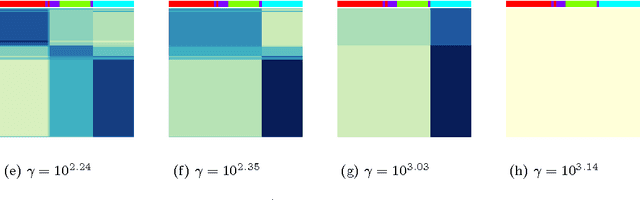
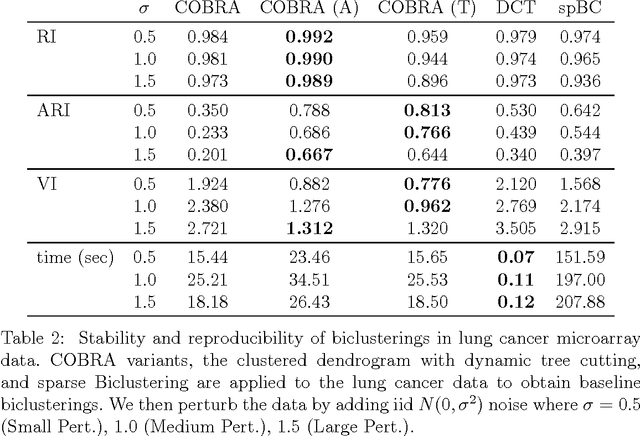
In the biclustering problem, we seek to simultaneously group observations and features. While biclustering has applications in a wide array of domains, ranging from text mining to collaborative filtering, the problem of identifying structure in high dimensional genomic data motivates this work. In this context, biclustering enables us to identify subsets of genes that are co-expressed only within a subset of experimental conditions. We present a convex formulation of the biclustering problem that possesses a unique global minimizer and an iterative algorithm, COBRA, that is guaranteed to identify it. Our approach generates an entire solution path of possible biclusters as a single tuning parameter is varied. We also show how to reduce the problem of selecting this tuning parameter to solving a trivial modification of the convex biclustering problem. The key contributions of our work are its simplicity, interpretability, and algorithmic guarantees - features that arguably are lacking in the current alternative algorithms. We demonstrate the advantages of our approach, which includes stably and reproducibly identifying biclusterings, on simulated and real microarray data.

Consistent Parameter Estimation for LASSO and Approximate Message Passing

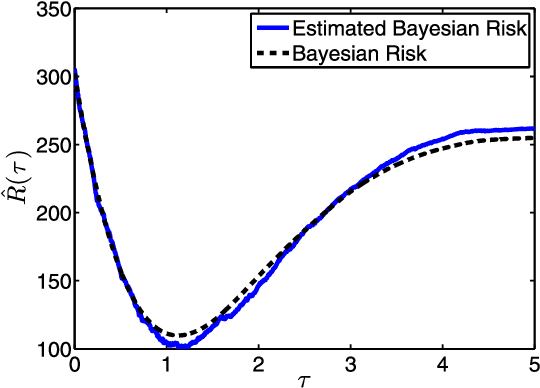
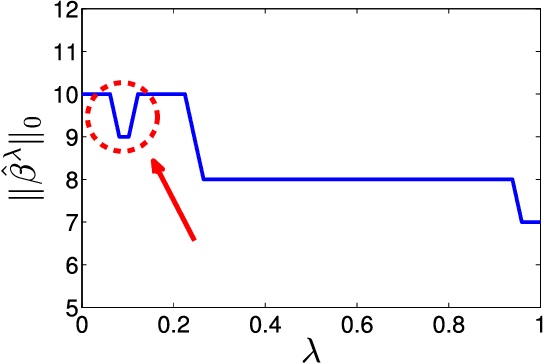
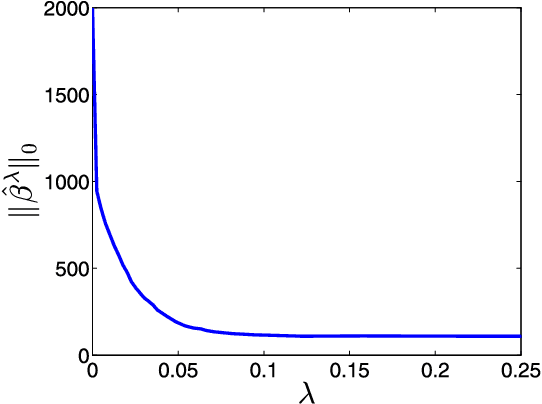
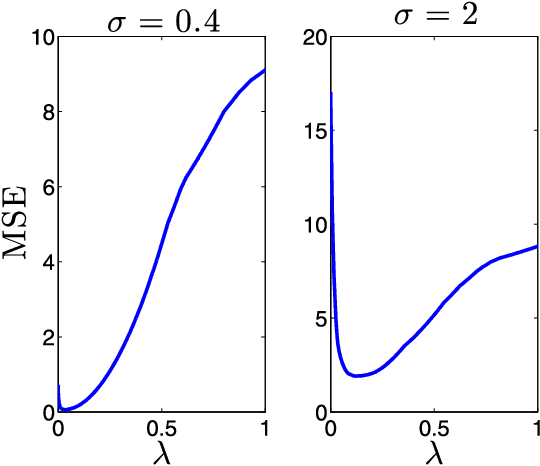
We consider the problem of recovering a vector $\beta_o \in \mathbb{R}^p$ from $n$ random and noisy linear observations $y= X\beta_o + w$, where $X$ is the measurement matrix and $w$ is noise. The LASSO estimate is given by the solution to the optimization problem $\hat{\beta}_{\lambda} = \arg \min_{\beta} \frac{1}{2} \|y-X\beta\|_2^2 + \lambda \| \beta \|_1$. Among the iterative algorithms that have been proposed for solving this optimization problem, approximate message passing (AMP) has attracted attention for its fast convergence. Despite significant progress in the theoretical analysis of the estimates of LASSO and AMP, little is known about their behavior as a function of the regularization parameter $\lambda$, or the thereshold parameters $\tau^t$. For instance the following basic questions have not yet been studied in the literature: (i) How does the size of the active set $\|\hat{\beta}^\lambda\|_0/p$ behave as a function of $\lambda$? (ii) How does the mean square error $\|\hat{\beta}_{\lambda} - \beta_o\|_2^2/p$ behave as a function of $\lambda$? (iii) How does $\|\beta^t - \beta_o \|_2^2/p$ behave as a function of $\tau^1, \ldots, \tau^{t-1}$? Answering these questions will help in addressing practical challenges regarding the optimal tuning of $\lambda$ or $\tau^1, \tau^2, \ldots$. This paper answers these questions in the asymptotic setting and shows how these results can be employed in deriving simple and theoretically optimal approaches for tuning the parameters $\tau^1, \ldots, \tau^t$ for AMP or $\lambda$ for LASSO. It also explores the connection between the optimal tuning of the parameters of AMP and the optimal tuning of LASSO.

A Deep Learning Approach to Structured Signal Recovery

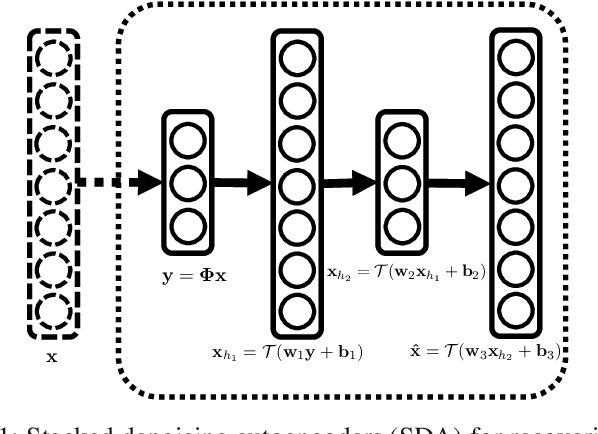
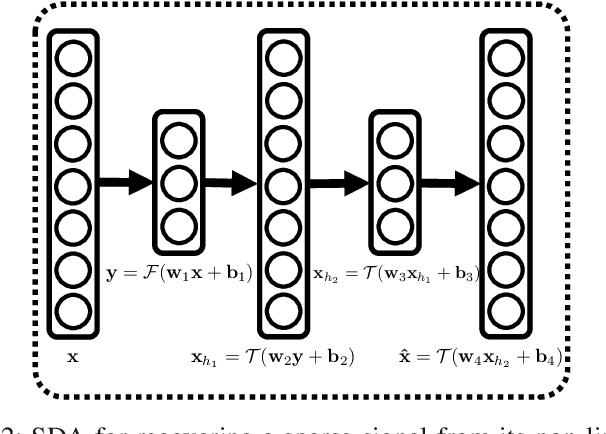
In this paper, we develop a new framework for sensing and recovering structured signals. In contrast to compressive sensing (CS) systems that employ linear measurements, sparse representations, and computationally complex convex/greedy algorithms, we introduce a deep learning framework that supports both linear and mildly nonlinear measurements, that learns a structured representation from training data, and that efficiently computes a signal estimate. In particular, we apply a stacked denoising autoencoder (SDA), as an unsupervised feature learner. SDA enables us to capture statistical dependencies between the different elements of certain signals and improve signal recovery performance as compared to the CS approach.

Video Compressive Sensing for Spatial Multiplexing Cameras using Motion-Flow Models

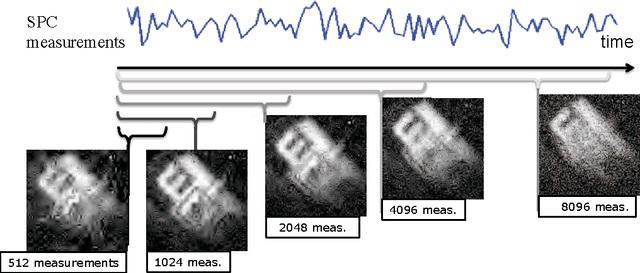
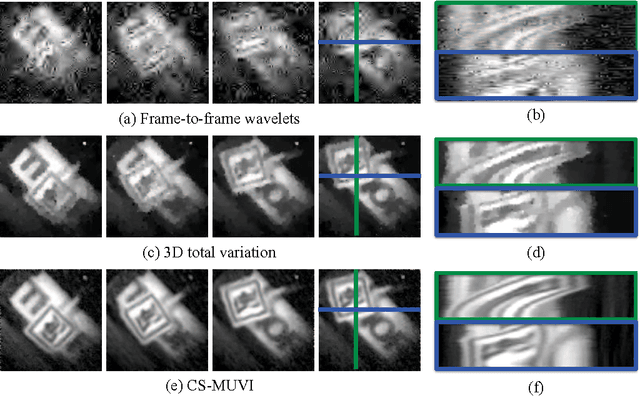
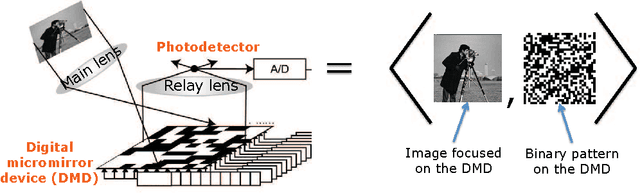
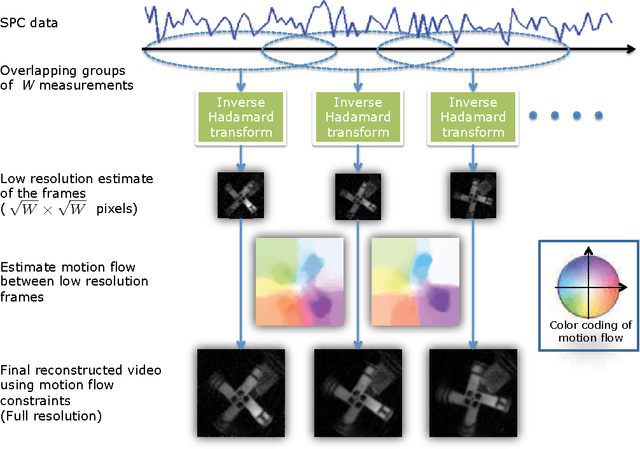
Spatial multiplexing cameras (SMCs) acquire a (typically static) scene through a series of coded projections using a spatial light modulator (e.g., a digital micro-mirror device) and a few optical sensors. This approach finds use in imaging applications where full-frame sensors are either too expensive (e.g., for short-wave infrared wavelengths) or unavailable. Existing SMC systems reconstruct static scenes using techniques from compressive sensing (CS). For videos, however, existing acquisition and recovery methods deliver poor quality. In this paper, we propose the CS multi-scale video (CS-MUVI) sensing and recovery framework for high-quality video acquisition and recovery using SMCs. Our framework features novel sensing matrices that enable the efficient computation of a low-resolution video preview, while enabling high-resolution video recovery using convex optimization. To further improve the quality of the reconstructed videos, we extract optical-flow estimates from the low-resolution previews and impose them as constraints in the recovery procedure. We demonstrate the efficacy of our CS-MUVI framework for a host of synthetic and real measured SMC video data, and we show that high-quality videos can be recovered at roughly $60\times$ compression.