oASIS: Adaptive Column Sampling for Kernel Matrix Approximation

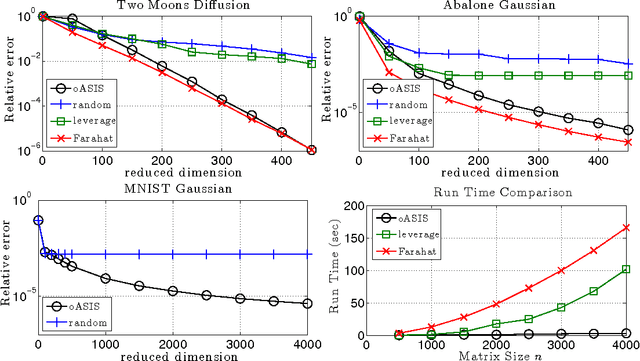
Kernel matrices (e.g. Gram or similarity matrices) are essential for many state-of-the-art approaches to classification, clustering, and dimensionality reduction. For large datasets, the cost of forming and factoring such kernel matrices becomes intractable. To address this challenge, we introduce a new adaptive sampling algorithm called Accelerated Sequential Incoherence Selection (oASIS) that samples columns without explicitly computing the entire kernel matrix. We provide conditions under which oASIS is guaranteed to exactly recover the kernel matrix with an optimal number of columns selected. Numerical experiments on both synthetic and real-world datasets demonstrate that oASIS achieves performance comparable to state-of-the-art adaptive sampling methods at a fraction of the computational cost. The low runtime complexity of oASIS and its low memory footprint enable the solution of large problems that are simply intractable using other adaptive methods.

Self-Expressive Decompositions for Matrix Approximation and Clustering

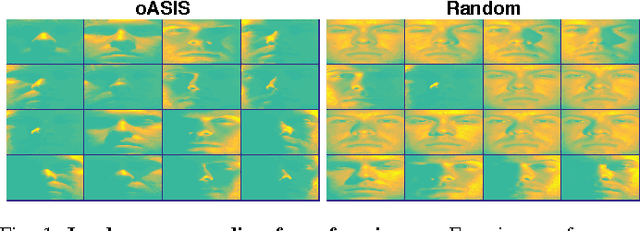
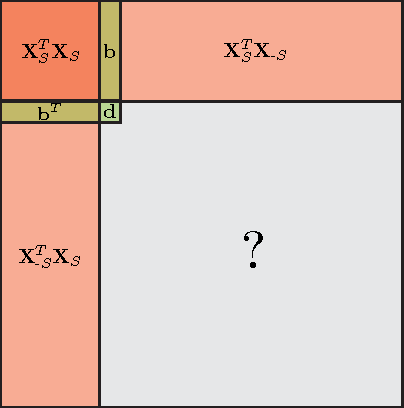
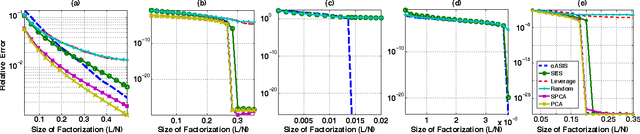
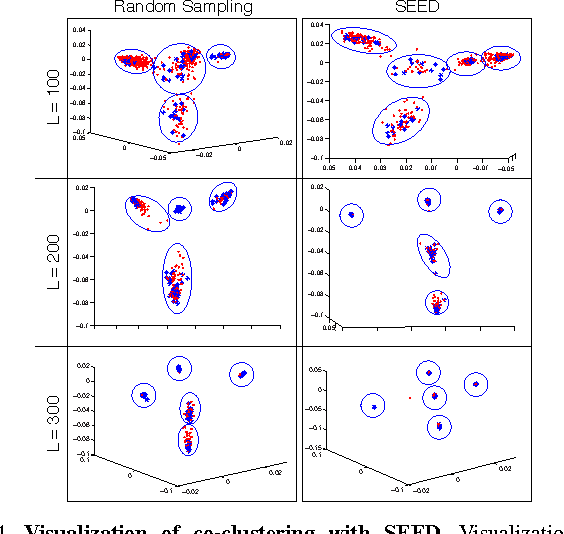
Data-aware methods for dimensionality reduction and matrix decomposition aim to find low-dimensional structure in a collection of data. Classical approaches discover such structure by learning a basis that can efficiently express the collection. Recently, "self expression", the idea of using a small subset of data vectors to represent the full collection, has been developed as an alternative to learning. Here, we introduce a scalable method for computing sparse SElf-Expressive Decompositions (SEED). SEED is a greedy method that constructs a basis by sequentially selecting incoherent vectors from the dataset. After forming a basis from a subset of vectors in the dataset, SEED then computes a sparse representation of the dataset with respect to this basis. We develop sufficient conditions under which SEED exactly represents low rank matrices and vectors sampled from a unions of independent subspaces. We show how SEED can be used in applications ranging from matrix approximation and denoising to clustering, and apply it to numerous real-world datasets. Our results demonstrate that SEED is an attractive low-complexity alternative to other sparse matrix factorization approaches such as sparse PCA and self-expressive methods for clustering.

A Probabilistic Theory of Deep Learning

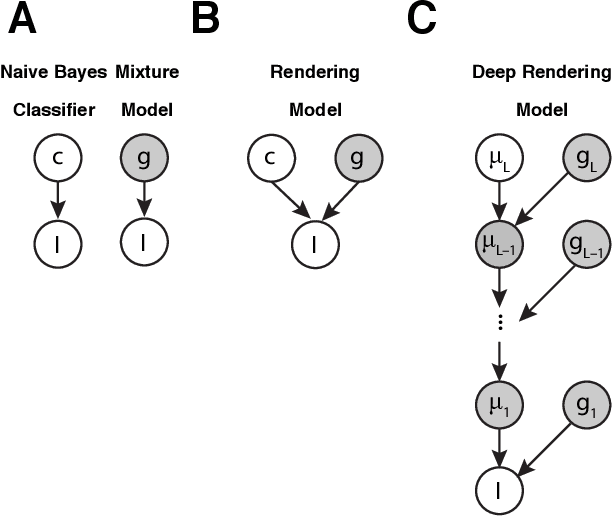
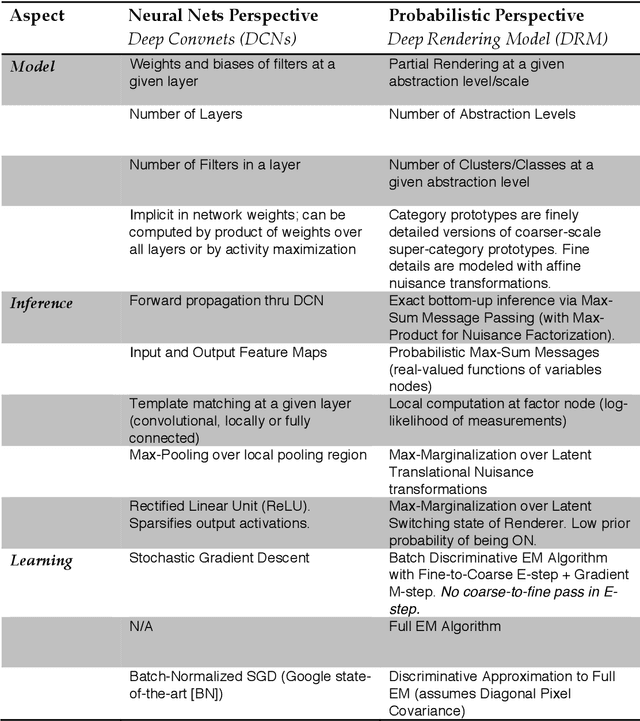
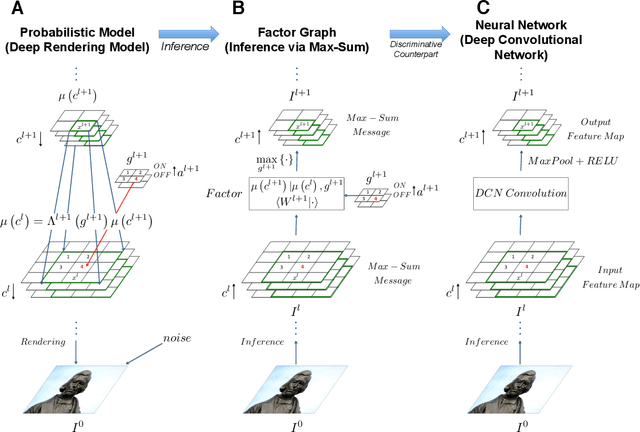
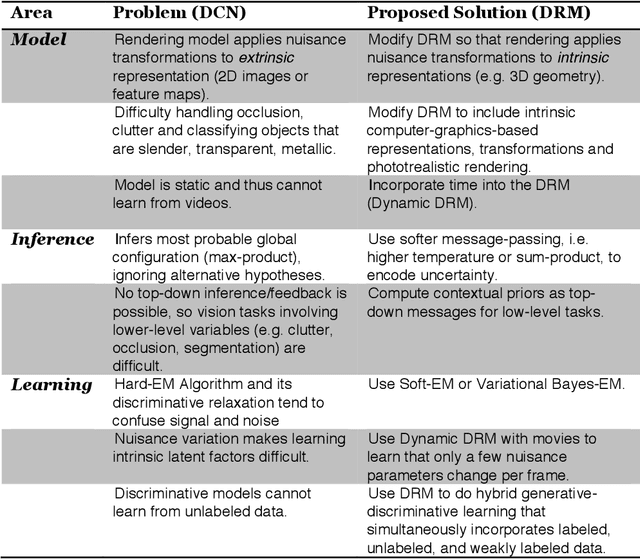
A grand challenge in machine learning is the development of computational algorithms that match or outperform humans in perceptual inference tasks that are complicated by nuisance variation. For instance, visual object recognition involves the unknown object position, orientation, and scale in object recognition while speech recognition involves the unknown voice pronunciation, pitch, and speed. Recently, a new breed of deep learning algorithms have emerged for high-nuisance inference tasks that routinely yield pattern recognition systems with near- or super-human capabilities. But a fundamental question remains: Why do they work? Intuitions abound, but a coherent framework for understanding, analyzing, and synthesizing deep learning architectures has remained elusive. We answer this question by developing a new probabilistic framework for deep learning based on the Deep Rendering Model: a generative probabilistic model that explicitly captures latent nuisance variation. By relaxing the generative model to a discriminative one, we can recover two of the current leading deep learning systems, deep convolutional neural networks and random decision forests, providing insights into their successes and shortcomings, as well as a principled route to their improvement.

Mathematical Language Processing: Automatic Grading and Feedback for Open Response Mathematical Questions

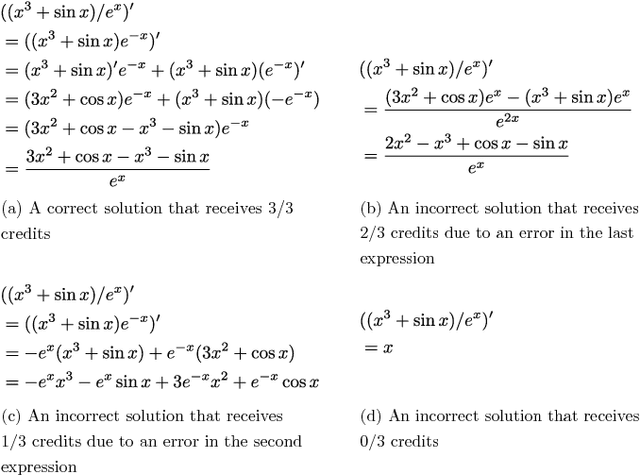
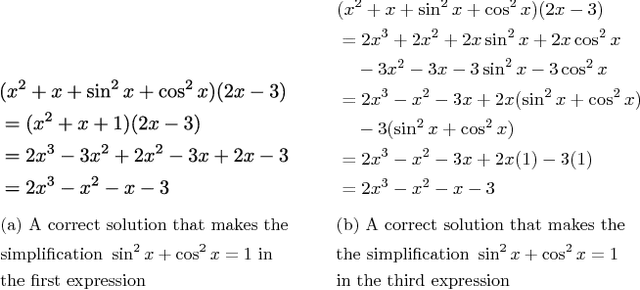
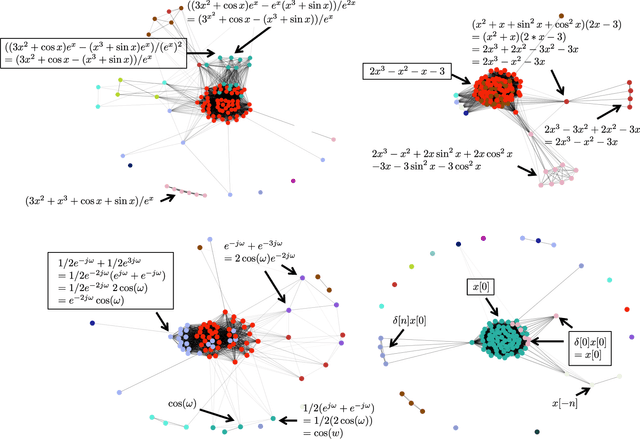
While computer and communication technologies have provided effective means to scale up many aspects of education, the submission and grading of assessments such as homework assignments and tests remains a weak link. In this paper, we study the problem of automatically grading the kinds of open response mathematical questions that figure prominently in STEM (science, technology, engineering, and mathematics) courses. Our data-driven framework for mathematical language processing (MLP) leverages solution data from a large number of learners to evaluate the correctness of their solutions, assign partial-credit scores, and provide feedback to each learner on the likely locations of any errors. MLP takes inspiration from the success of natural language processing for text data and comprises three main steps. First, we convert each solution to an open response mathematical question into a series of numerical features. Second, we cluster the features from several solutions to uncover the structures of correct, partially correct, and incorrect solutions. We develop two different clustering approaches, one that leverages generic clustering algorithms and one based on Bayesian nonparametrics. Third, we automatically grade the remaining (potentially large number of) solutions based on their assigned cluster and one instructor-provided grade per cluster. As a bonus, we can track the cluster assignment of each step of a multistep solution and determine when it departs from a cluster of correct solutions, which enables us to indicate the likely locations of errors to learners. We test and validate MLP on real-world MOOC data to demonstrate how it can substantially reduce the human effort required in large-scale educational platforms.

SPRITE: A Response Model For Multiple Choice Testing

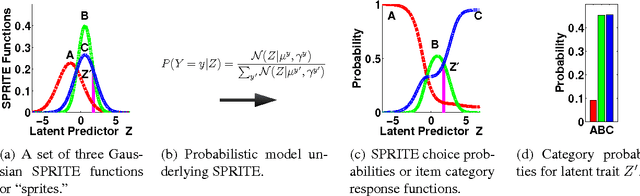
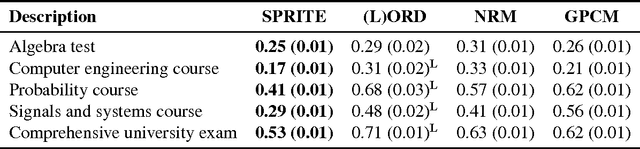
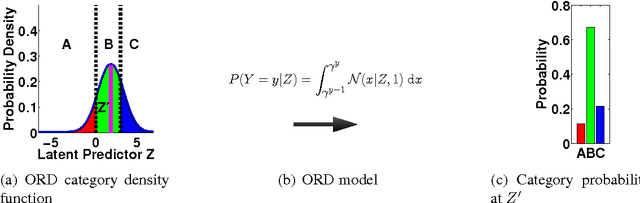
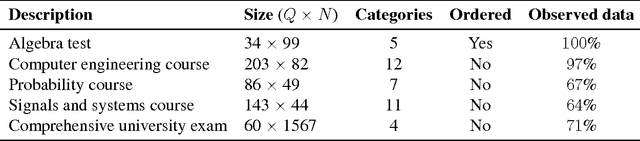
Item response theory (IRT) models for categorical response data are widely used in the analysis of educational data, computerized adaptive testing, and psychological surveys. However, most IRT models rely on both the assumption that categories are strictly ordered and the assumption that this ordering is known a priori. These assumptions are impractical in many real-world scenarios, such as multiple-choice exams where the levels of incorrectness for the distractor categories are often unknown. While a number of results exist on IRT models for unordered categorical data, they tend to have restrictive modeling assumptions that lead to poor data fitting performance in practice. Furthermore, existing unordered categorical models have parameters that are difficult to interpret. In this work, we propose a novel methodology for unordered categorical IRT that we call SPRITE (short for stochastic polytomous response item model) that: (i) analyzes both ordered and unordered categories, (ii) offers interpretable outputs, and (iii) provides improved data fitting compared to existing models. We compare SPRITE to existing item response models and demonstrate its efficacy on both synthetic and real-world educational datasets.

Quantized Matrix Completion for Personalized Learning

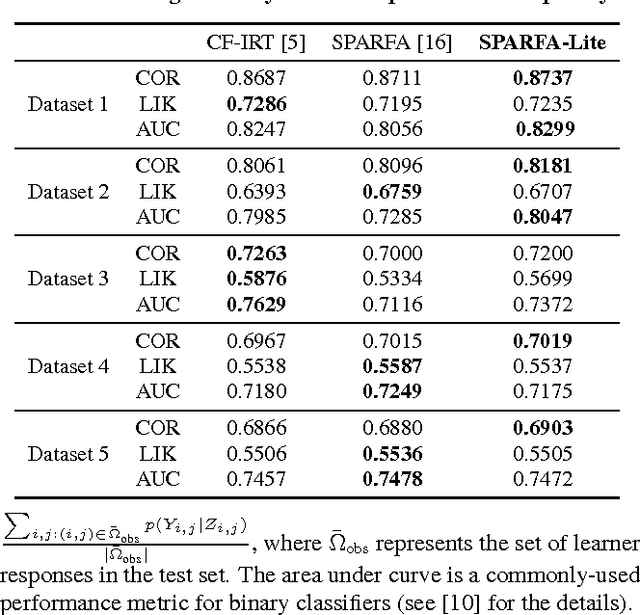
The recently proposed SPARse Factor Analysis (SPARFA) framework for personalized learning performs factor analysis on ordinal or binary-valued (e.g., correct/incorrect) graded learner responses to questions. The underlying factors are termed "concepts" (or knowledge components) and are used for learning analytics (LA), the estimation of learner concept-knowledge profiles, and for content analytics (CA), the estimation of question-concept associations and question difficulties. While SPARFA is a powerful tool for LA and CA, it requires a number of algorithm parameters (including the number of concepts), which are difficult to determine in practice. In this paper, we propose SPARFA-Lite, a convex optimization-based method for LA that builds on matrix completion, which only requires a single algorithm parameter and enables us to automatically identify the required number of concepts. Using a variety of educational datasets, we demonstrate that SPARFALite (i) achieves comparable performance in predicting unobserved learner responses to existing methods, including item response theory (IRT) and SPARFA, and (ii) is computationally more efficient.

Tag-Aware Ordinal Sparse Factor Analysis for Learning and Content Analytics

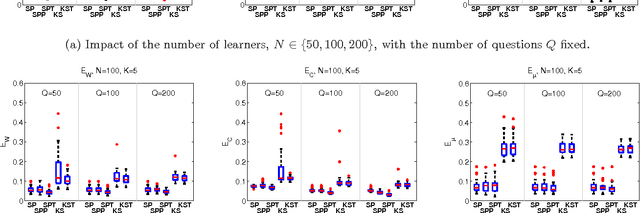
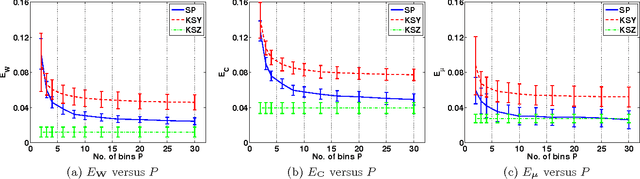
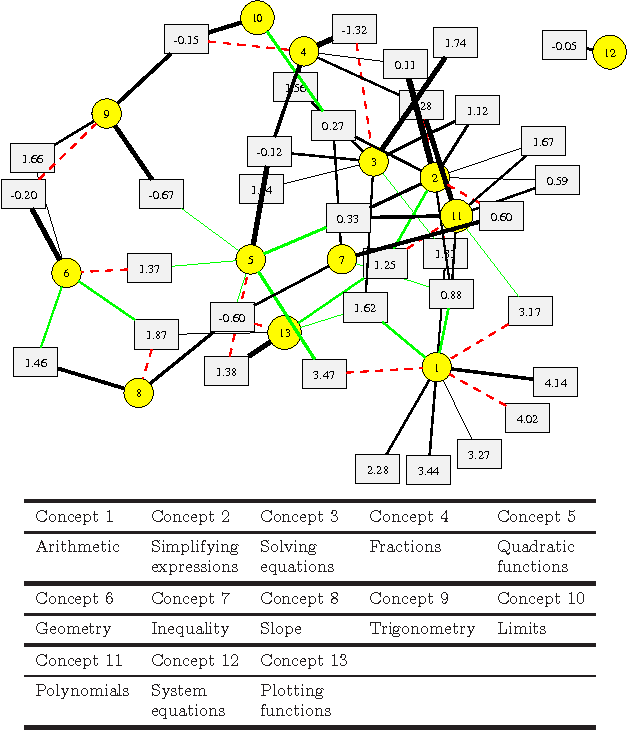
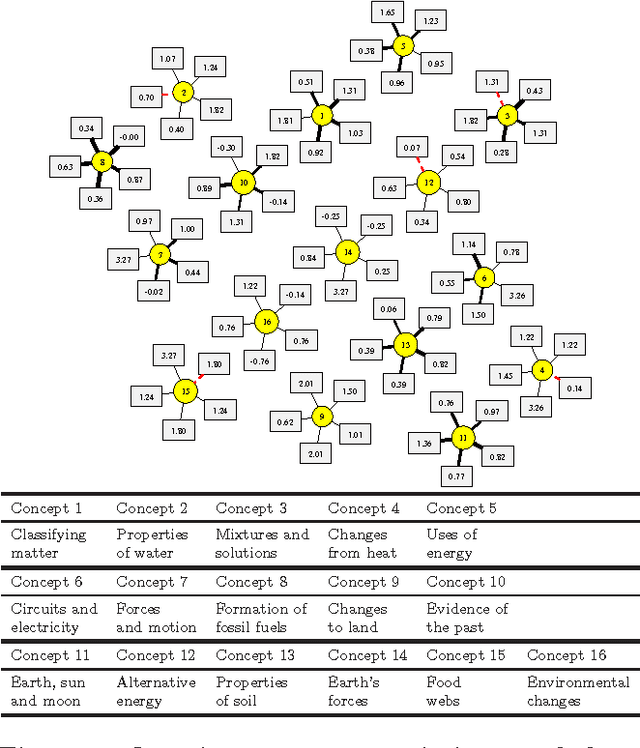
Machine learning offers novel ways and means to design personalized learning systems wherein each student's educational experience is customized in real time depending on their background, learning goals, and performance to date. SPARse Factor Analysis (SPARFA) is a novel framework for machine learning-based learning analytics, which estimates a learner's knowledge of the concepts underlying a domain, and content analytics, which estimates the relationships among a collection of questions and those concepts. SPARFA jointly learns the associations among the questions and the concepts, learner concept knowledge profiles, and the underlying question difficulties, solely based on the correct/incorrect graded responses of a population of learners to a collection of questions. In this paper, we extend the SPARFA framework significantly to enable: (i) the analysis of graded responses on an ordinal scale (partial credit) rather than a binary scale (correct/incorrect); (ii) the exploitation of tags/labels for questions that partially describe the question{concept associations. The resulting Ordinal SPARFA-Tag framework greatly enhances the interpretability of the estimated concepts. We demonstrate using real educational data that Ordinal SPARFA-Tag outperforms both SPARFA and existing collaborative filtering techniques in predicting missing learner responses.

Sparse Bilinear Logistic Regression

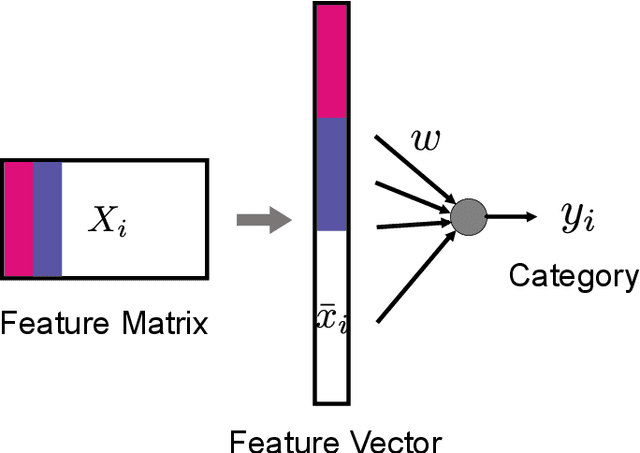
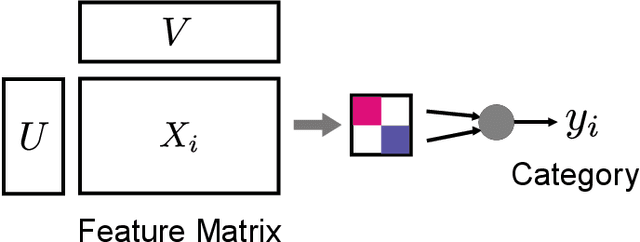
In this paper, we introduce the concept of sparse bilinear logistic regression for decision problems involving explanatory variables that are two-dimensional matrices. Such problems are common in computer vision, brain-computer interfaces, style/content factorization, and parallel factor analysis. The underlying optimization problem is bi-convex; we study its solution and develop an efficient algorithm based on block coordinate descent. We provide a theoretical guarantee for global convergence and estimate the asymptotical convergence rate using the Kurdyka-{\L}ojasiewicz inequality. A range of experiments with simulated and real data demonstrate that sparse bilinear logistic regression outperforms current techniques in several important applications.

Active Learning for Undirected Graphical Model Selection

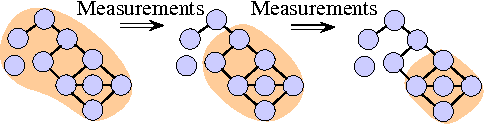
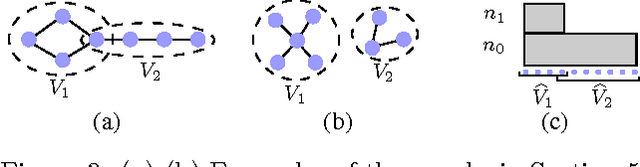
This paper studies graphical model selection, i.e., the problem of estimating a graph of statistical relationships among a collection of random variables. Conventional graphical model selection algorithms are passive, i.e., they require all the measurements to have been collected before processing begins. We propose an active learning algorithm that uses junction tree representations to adapt future measurements based on the information gathered from prior measurements. We prove that, under certain conditions, our active learning algorithm requires fewer scalar measurements than any passive algorithm to reliably estimate a graph. A range of numerical results validate our theory and demonstrates the benefits of active learning.

Path Thresholding: Asymptotically Tuning-Free High-Dimensional Sparse Regression

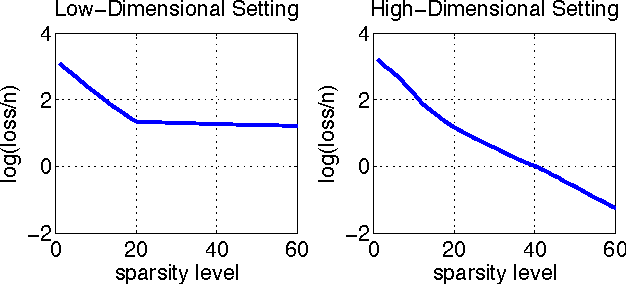
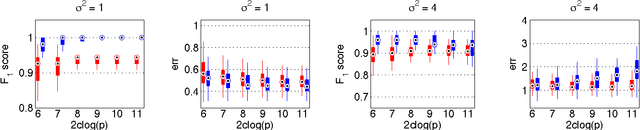
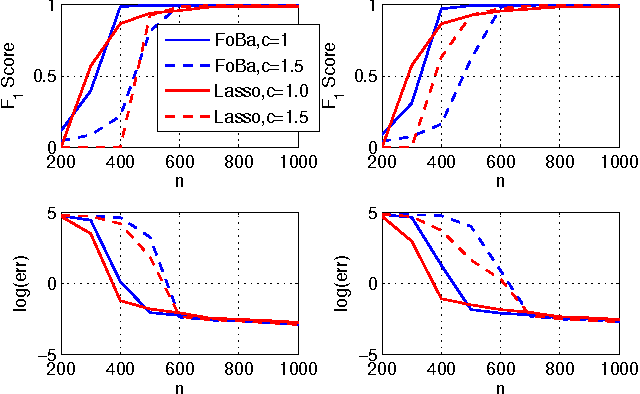
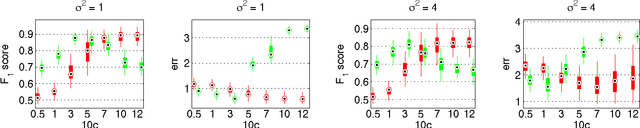
In this paper, we address the challenging problem of selecting tuning parameters for high-dimensional sparse regression. We propose a simple and computationally efficient method, called path thresholding (PaTh), that transforms any tuning parameter-dependent sparse regression algorithm into an asymptotically tuning-free sparse regression algorithm. More specifically, we prove that, as the problem size becomes large (in the number of variables and in the number of observations), PaTh performs accurate sparse regression, under appropriate conditions, without specifying a tuning parameter. In finite-dimensional settings, we demonstrate that PaTh can alleviate the computational burden of model selection algorithms by significantly reducing the search space of tuning parameters.