Sparse Bilinear Logistic Regression

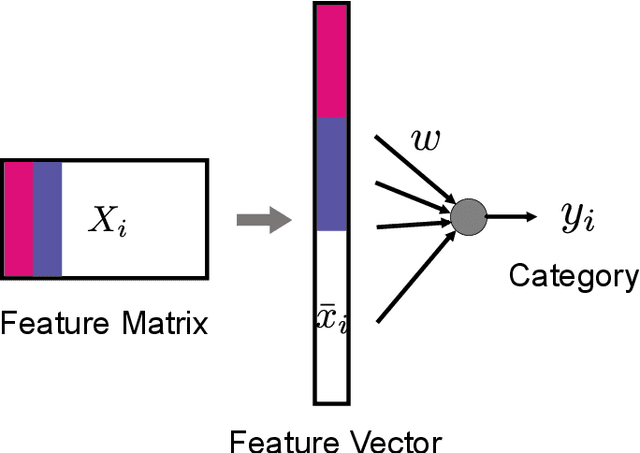
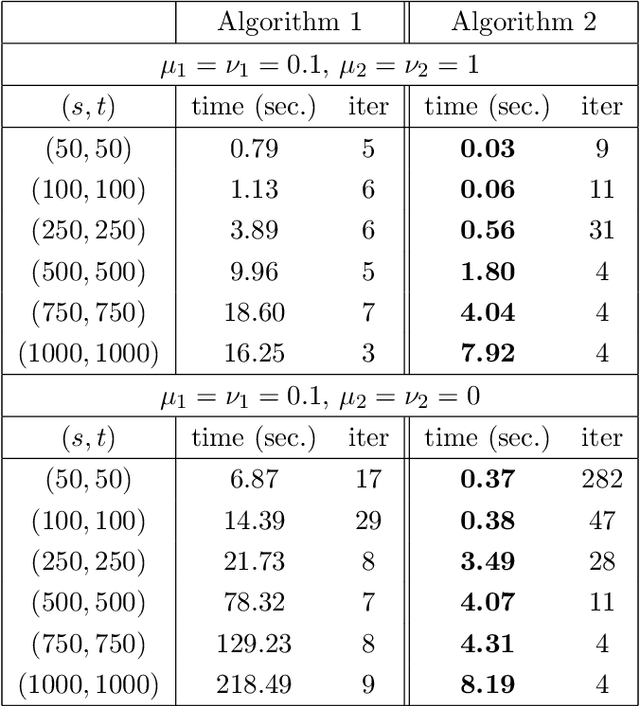
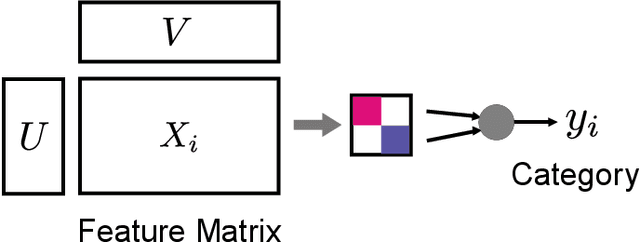
In this paper, we introduce the concept of sparse bilinear logistic regression for decision problems involving explanatory variables that are two-dimensional matrices. Such problems are common in computer vision, brain-computer interfaces, style/content factorization, and parallel factor analysis. The underlying optimization problem is bi-convex; we study its solution and develop an efficient algorithm based on block coordinate descent. We provide a theoretical guarantee for global convergence and estimate the asymptotical convergence rate using the Kurdyka-{\L}ojasiewicz inequality. A range of experiments with simulated and real data demonstrate that sparse bilinear logistic regression outperforms current techniques in several important applications.

Video Compressive Sensing for Dynamic MRI

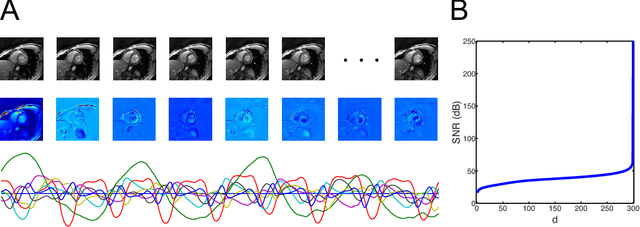
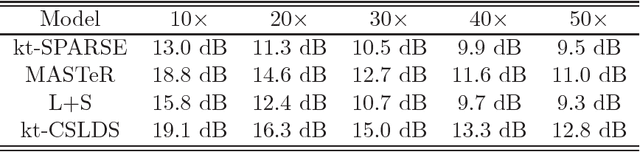
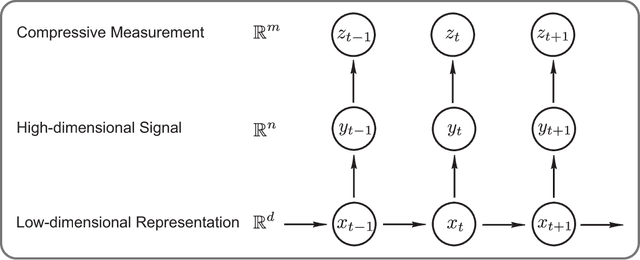
We present a video compressive sensing framework, termed kt-CSLDS, to accelerate the image acquisition process of dynamic magnetic resonance imaging (MRI). We are inspired by a state-of-the-art model for video compressive sensing that utilizes a linear dynamical system (LDS) to model the motion manifold. Given compressive measurements, the state sequence of an LDS can be first estimated using system identification techniques. We then reconstruct the observation matrix using a joint structured sparsity assumption. In particular, we minimize an objective function with a mixture of wavelet sparsity and joint sparsity within the observation matrix. We derive an efficient convex optimization algorithm through alternating direction method of multipliers (ADMM), and provide a theoretical guarantee for global convergence. We demonstrate the performance of our approach for video compressive sensing, in terms of reconstruction accuracy. We also investigate the impact of various sampling strategies. We apply this framework to accelerate the acquisition process of dynamic MRI and show it achieves the best reconstruction accuracy with the least computational time compared with existing algorithms in the literature.