Raajen Patel
oASIS: Adaptive Column Sampling for Kernel Matrix Approximation
May 19, 2015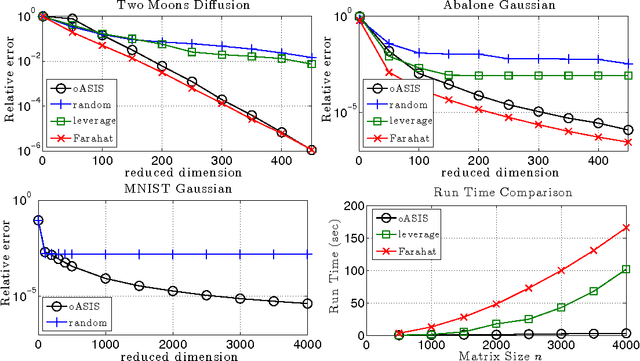

Abstract:Kernel matrices (e.g. Gram or similarity matrices) are essential for many state-of-the-art approaches to classification, clustering, and dimensionality reduction. For large datasets, the cost of forming and factoring such kernel matrices becomes intractable. To address this challenge, we introduce a new adaptive sampling algorithm called Accelerated Sequential Incoherence Selection (oASIS) that samples columns without explicitly computing the entire kernel matrix. We provide conditions under which oASIS is guaranteed to exactly recover the kernel matrix with an optimal number of columns selected. Numerical experiments on both synthetic and real-world datasets demonstrate that oASIS achieves performance comparable to state-of-the-art adaptive sampling methods at a fraction of the computational cost. The low runtime complexity of oASIS and its low memory footprint enable the solution of large problems that are simply intractable using other adaptive methods.
Self-Expressive Decompositions for Matrix Approximation and Clustering
May 04, 2015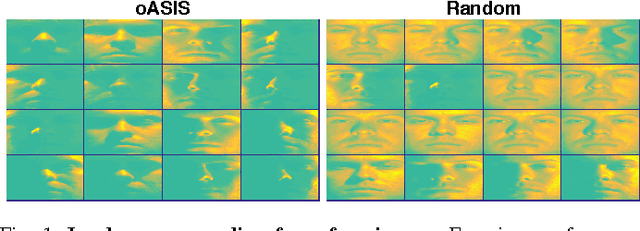
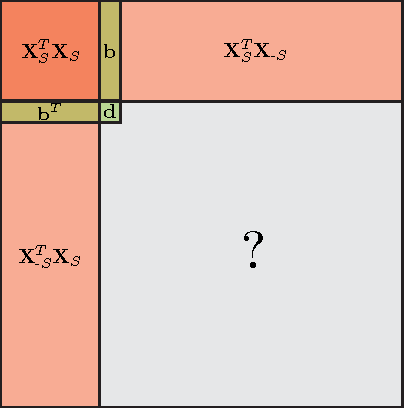
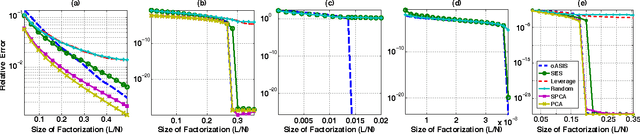
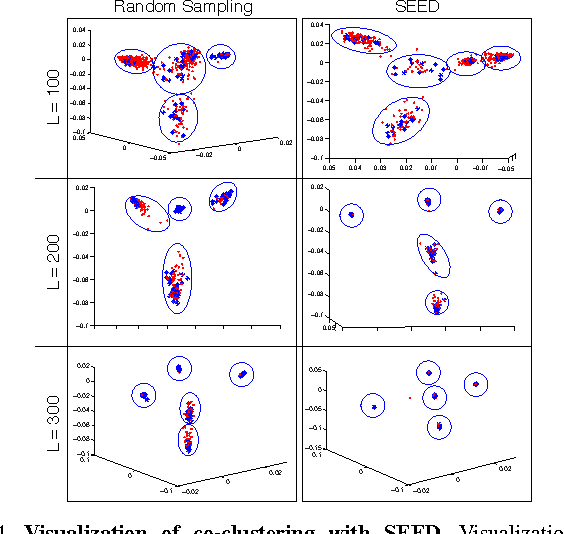
Abstract:Data-aware methods for dimensionality reduction and matrix decomposition aim to find low-dimensional structure in a collection of data. Classical approaches discover such structure by learning a basis that can efficiently express the collection. Recently, "self expression", the idea of using a small subset of data vectors to represent the full collection, has been developed as an alternative to learning. Here, we introduce a scalable method for computing sparse SElf-Expressive Decompositions (SEED). SEED is a greedy method that constructs a basis by sequentially selecting incoherent vectors from the dataset. After forming a basis from a subset of vectors in the dataset, SEED then computes a sparse representation of the dataset with respect to this basis. We develop sufficient conditions under which SEED exactly represents low rank matrices and vectors sampled from a unions of independent subspaces. We show how SEED can be used in applications ranging from matrix approximation and denoising to clustering, and apply it to numerous real-world datasets. Our results demonstrate that SEED is an attractive low-complexity alternative to other sparse matrix factorization approaches such as sparse PCA and self-expressive methods for clustering.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge