"Rebuilding" Statistics in the Age of AI: A Town Hall Discussion on Culture, Infrastructure, and Training

This article presents the full, original record of the 2024 Joint Statistical Meetings (JSM) town hall, "Statistics in the Age of AI," which convened leading statisticians to discuss how the field is evolving in response to advances in artificial intelligence, foundation models, large-scale empirical modeling, and data-intensive infrastructures. The town hall was structured around open panel discussion and extensive audience Q&A, with the aim of eliciting candid, experience-driven perspectives rather than formal presentations or prepared statements. This document preserves the extended exchanges among panelists and audience members, with minimal editorial intervention, and organizes the conversation around five recurring questions concerning disciplinary culture and practices, data curation and "data work," engagement with modern empirical modeling, training for large-scale AI applications, and partnerships with key AI stakeholders. By providing an archival record of this discussion, the preprint aims to support transparency, community reflection, and ongoing dialogue about the evolving role of statistics in the data- and AI-centric future.

Stability of Density-Based Clustering

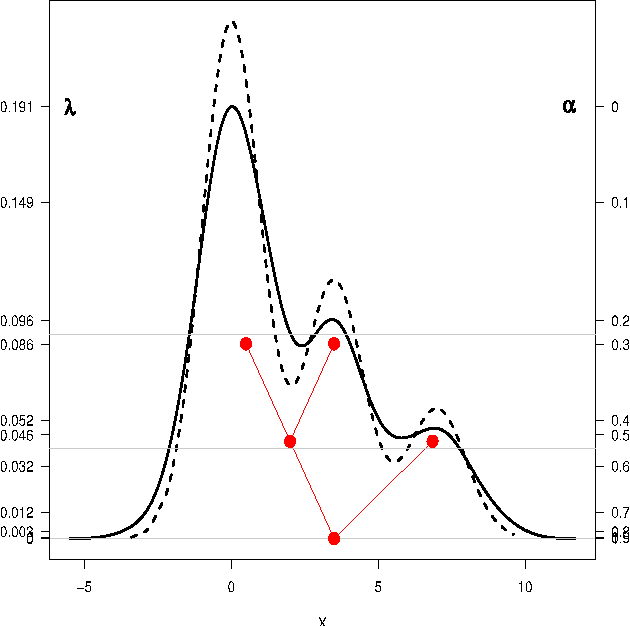
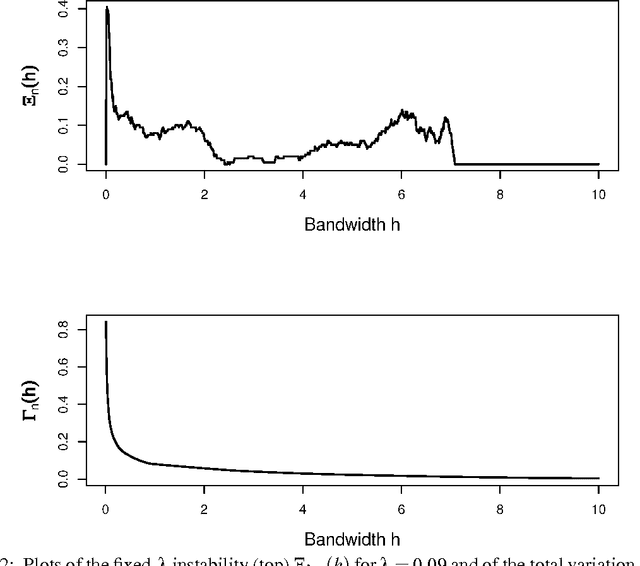
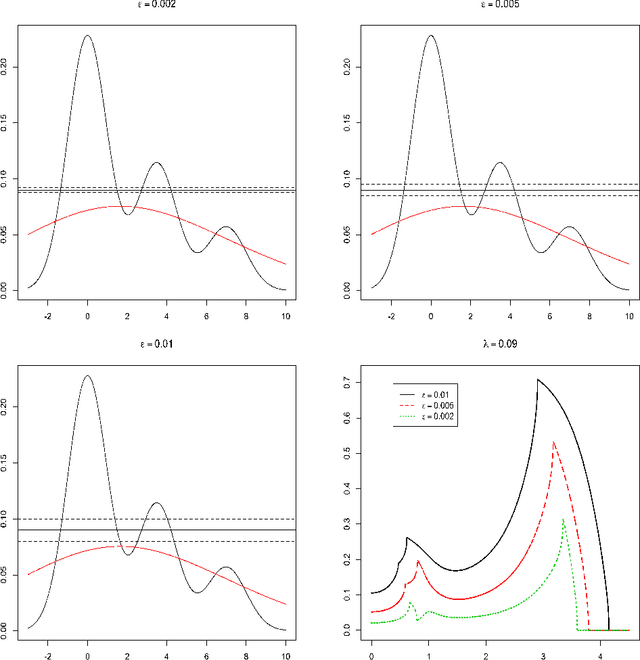
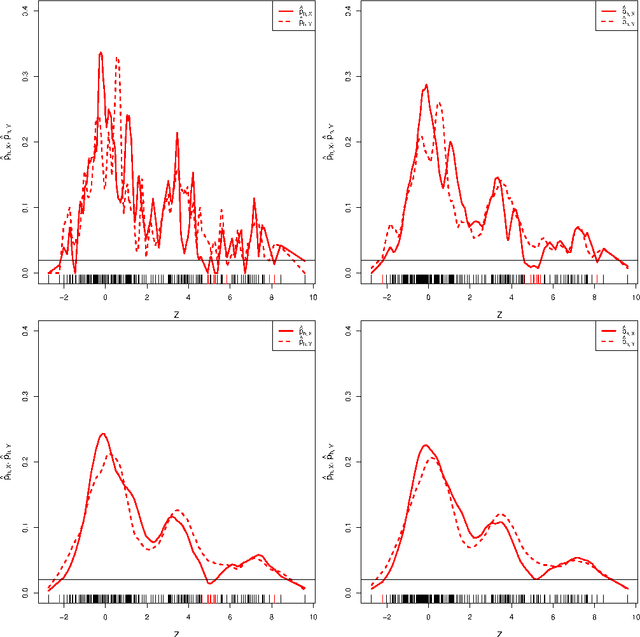
High density clusters can be characterized by the connected components of a level set $L(\lambda) = \{x:\ p(x)>\lambda\}$ of the underlying probability density function $p$ generating the data, at some appropriate level $\lambda\geq 0$. The complete hierarchical clustering can be characterized by a cluster tree ${\cal T}= \bigcup_{\lambda} L(\lambda)$. In this paper, we study the behavior of a density level set estimate $\widehat L(\lambda)$ and cluster tree estimate $\widehat{\cal{T}}$ based on a kernel density estimator with kernel bandwidth $h$. We define two notions of instability to measure the variability of $\widehat L(\lambda)$ and $\widehat{\cal{T}}$ as a function of $h$, and investigate the theoretical properties of these instability measures.