Dimension-reduced outcome-weighted learning for estimating individualized treatment regimes in observational studies

Individualized treatment regimes (ITRs) aim to improve clinical outcomes by assigning treatment based on patient-specific characteristics. However, existing methods often struggle with high-dimensional covariates, limiting accuracy, interpretability, and real-world applicability. We propose a novel sufficient dimension reduction approach that directly targets the contrast between potential outcomes and identifies a low-dimensional subspace of the covariates capturing treatment effect heterogeneity. This reduced representation enables more accurate estimation of optimal ITRs through outcome-weighted learning. To accommodate observational data, our method incorporates kernel-based covariate balancing, allowing treatment assignment to depend on the full covariate set and avoiding the restrictive assumption that the subspace sufficient for modeling heterogeneous treatment effects is also sufficient for confounding adjustment. We show that the proposed method achieves universal consistency, i.e., its risk converges to the Bayes risk, under mild regularity conditions. We demonstrate its finite sample performance through simulations and an analysis of intensive care unit sepsis patient data to determine who should receive transthoracic echocardiography.

Matrix Completion with Model-free Weighting

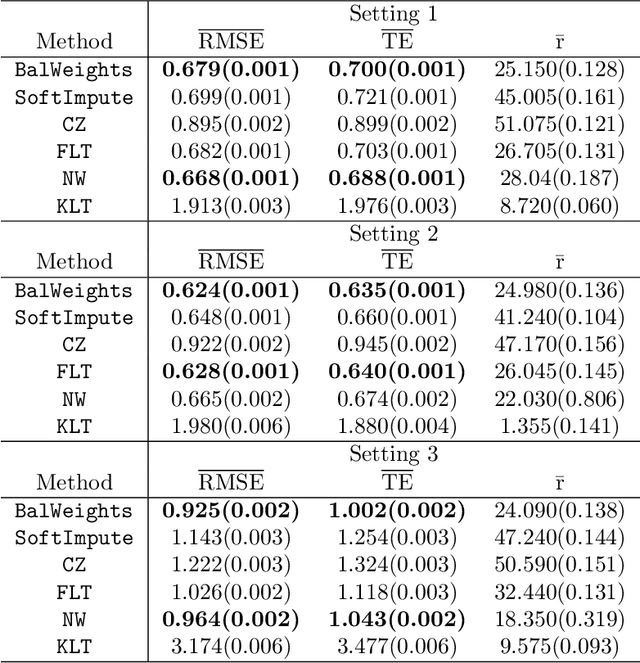
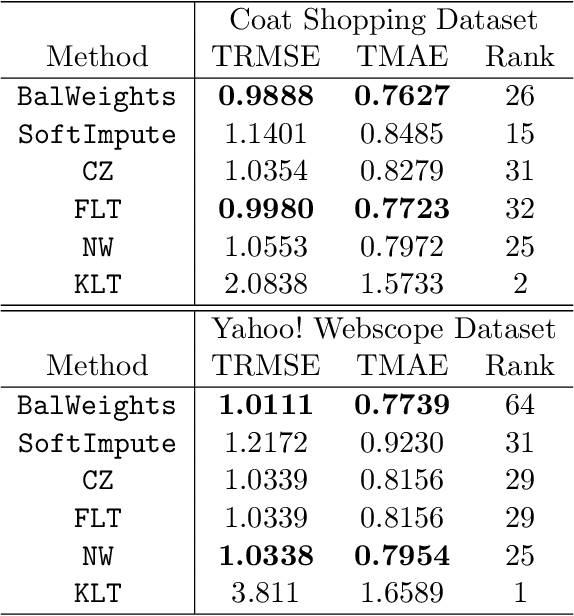
In this paper, we propose a novel method for matrix completion under general non-uniform missing structures. By controlling an upper bound of a novel balancing error, we construct weights that can actively adjust for the non-uniformity in the empirical risk without explicitly modeling the observation probabilities, and can be computed efficiently via convex optimization. The recovered matrix based on the proposed weighted empirical risk enjoys appealing theoretical guarantees. In particular, the proposed method achieves a stronger guarantee than existing work in terms of the scaling with respect to the observation probabilities, under asymptotically heterogeneous missing settings (where entry-wise observation probabilities can be of different orders). These settings can be regarded as a better theoretical model of missing patterns with highly varying probabilities. We also provide a new minimax lower bound under a class of heterogeneous settings. Numerical experiments are also provided to demonstrate the effectiveness of the proposed method.