Rajen D. Shah
The Projected Covariance Measure for assumption-lean variable significance testing
Nov 03, 2022


Abstract:Testing the significance of a variable or group of variables $X$ for predicting a response $Y$, given additional covariates $Z$, is a ubiquitous task in statistics. A simple but common approach is to specify a linear model, and then test whether the regression coefficient for $X$ is non-zero. However, when the model is misspecified, the test may have poor power, for example when $X$ is involved in complex interactions, or lead to many false rejections. In this work we study the problem of testing the model-free null of conditional mean independence, i.e. that the conditional mean of $Y$ given $X$ and $Z$ does not depend on $X$. We propose a simple and general framework that can leverage flexible nonparametric or machine learning methods, such as additive models or random forests, to yield both robust error control and high power. The procedure involves using these methods to perform regressions, first to estimate a form of projection of $Y$ on $X$ and $Z$ using one half of the data, and then to estimate the expected conditional covariance between this projection and $Y$ on the remaining half of the data. While the approach is general, we show that a version of our procedure using spline regression achieves what we show is the minimax optimal rate in this nonparametric testing problem. Numerical experiments demonstrate the effectiveness of our approach both in terms of maintaining Type I error control, and power, compared to several existing approaches.
Cross-validation for change-point regression: pitfalls and solutions
Dec 06, 2021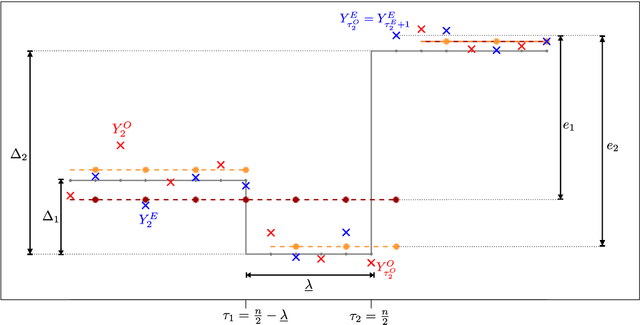
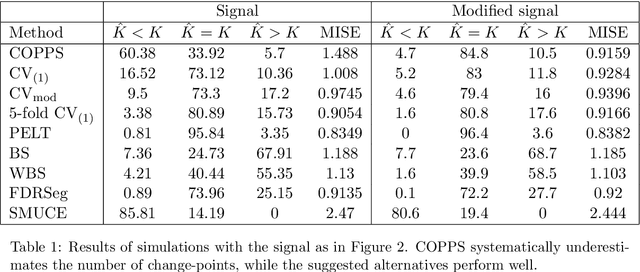
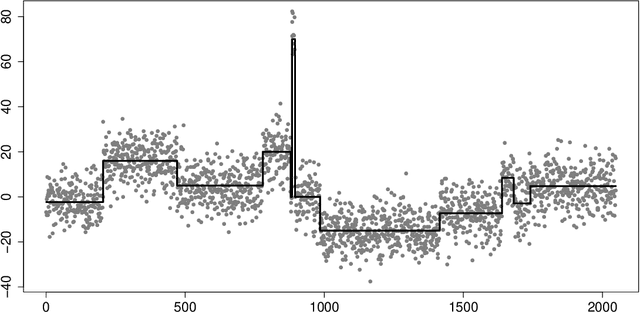
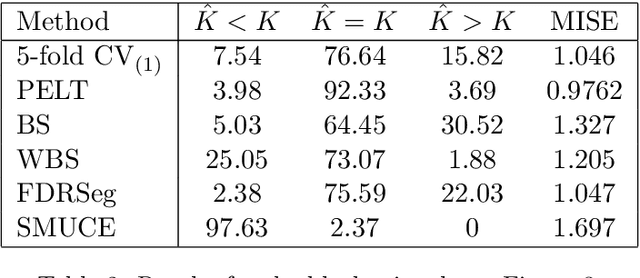
Abstract:Cross-validation is the standard approach for tuning parameter selection in many non-parametric regression problems. However its use is less common in change-point regression, perhaps as its prediction error-based criterion may appear to permit small spurious changes and hence be less well-suited to estimation of the number and location of change-points. We show that in fact the problems of cross-validation with squared error loss are more severe and can lead to systematic under- or over-estimation of the number of change-points, and highly suboptimal estimation of the mean function in simple settings where changes are easily detectable. We propose two simple approaches to remedy these issues, the first involving the use of absolute error rather than squared error loss, and the second involving modifying the holdout sets used. For the latter, we provide conditions that permit consistent estimation of the number of change-points for a general change-point estimation procedure. We show these conditions are satisfied for optimal partitioning using new results on its performance when supplied with the incorrect number of change-points. Numerical experiments show that the absolute error approach in particular is competitive with common change-point methods using classical tuning parameter choices when error distributions are well-specified, but can substantially outperform these in misspecified models. An implementation of our methodology is available in the R package crossvalidationCP on CRAN.
High-dimensional regression with potential prior information on variable importance
Sep 23, 2021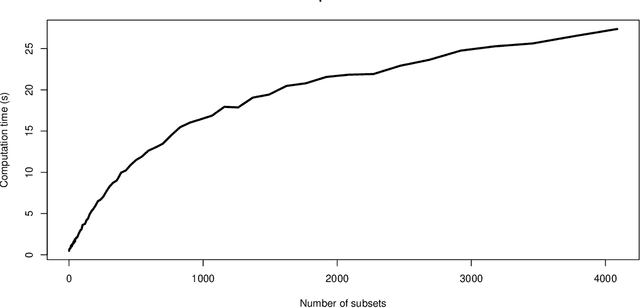
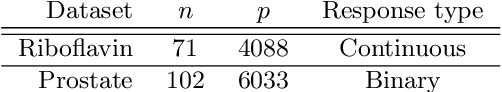
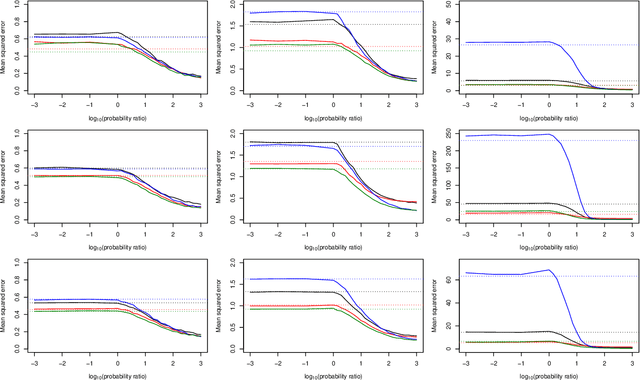
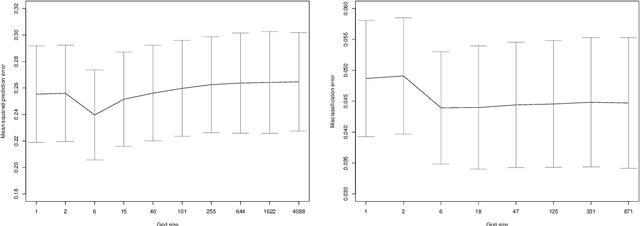
Abstract:There are a variety of settings where vague prior information may be available on the importance of predictors in high-dimensional regression settings. Examples include ordering on the variables offered by their empirical variances (which is typically discarded through standardisation), the lag of predictors when fitting autoregressive models in time series settings, or the level of missingness of the variables. Whilst such orderings may not match the true importance of variables, we argue that there is little to be lost, and potentially much to be gained, by using them. We propose a simple scheme involving fitting a sequence of models indicated by the ordering. We show that the computational cost for fitting all models when ridge regression is used is no more than for a single fit of ridge regression, and describe a strategy for Lasso regression that makes use of previous fits to greatly speed up fitting the entire sequence of models. We propose to select a final estimator by cross-validation and provide a general result on the quality of the best performing estimator on a test set selected from among a number $M$ of competing estimators in a high-dimensional linear regression setting. Our result requires no sparsity assumptions and shows that only a $\log M$ price is incurred compared to the unknown best estimator. We demonstrate the effectiveness of our approach when applied to missing or corrupted data, and time series settings. An R package is available on github.
Structure Learning for Directed Trees
Aug 19, 2021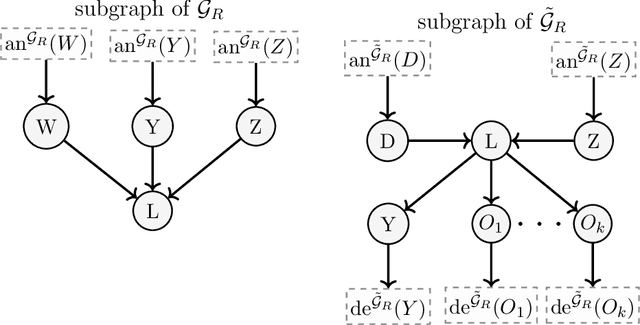
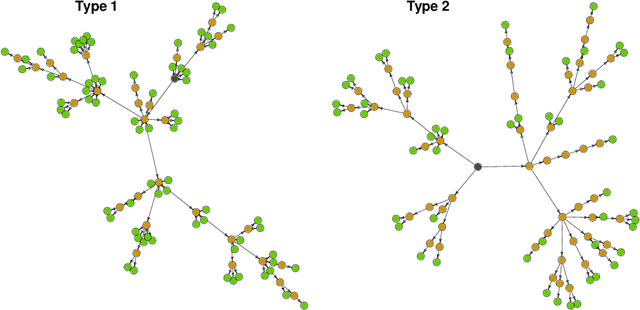
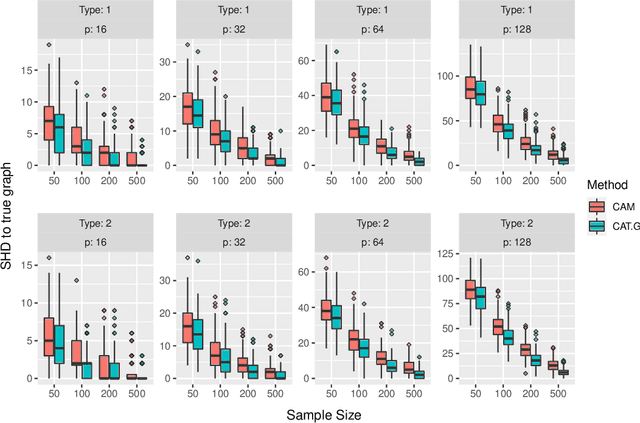
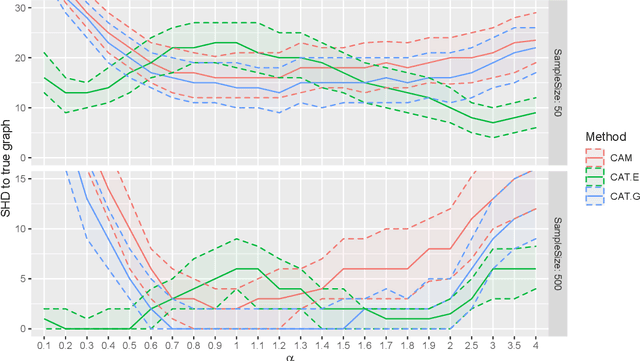
Abstract:Knowing the causal structure of a system is of fundamental interest in many areas of science and can aid the design of prediction algorithms that work well under manipulations to the system. The causal structure becomes identifiable from the observational distribution under certain restrictions. To learn the structure from data, score-based methods evaluate different graphs according to the quality of their fits. However, for large nonlinear models, these rely on heuristic optimization approaches with no general guarantees of recovering the true causal structure. In this paper, we consider structure learning of directed trees. We propose a fast and scalable method based on Chu-Liu-Edmonds' algorithm we call causal additive trees (CAT). For the case of Gaussian errors, we prove consistency in an asymptotic regime with a vanishing identifiability gap. We also introduce a method for testing substructure hypotheses with asymptotic family-wise error rate control that is valid post-selection and in unidentified settings. Furthermore, we study the identifiability gap, which quantifies how much better the true causal model fits the observational distribution, and prove that it is lower bounded by local properties of the causal model. Simulation studies demonstrate the favorable performance of CAT compared to competing structure learning methods.
Modelling High-Dimensional Categorical Data Using Nonconvex Fusion Penalties
Feb 28, 2020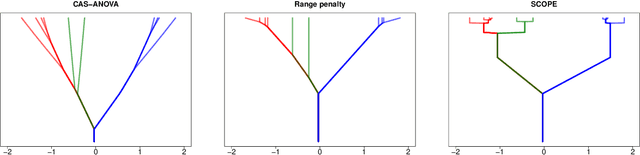
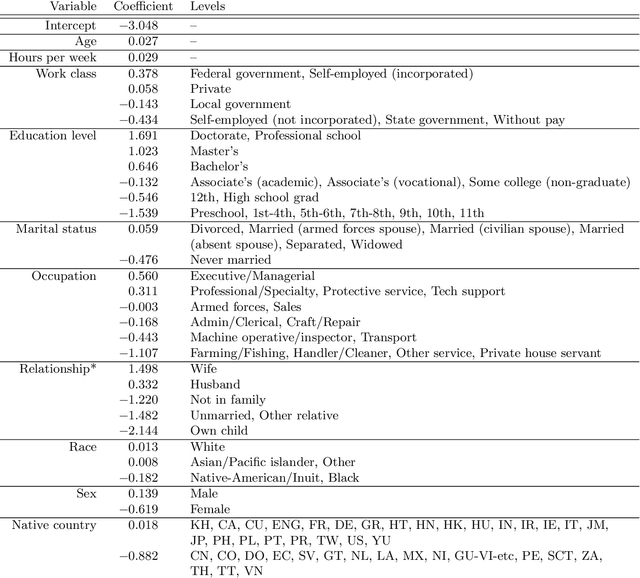
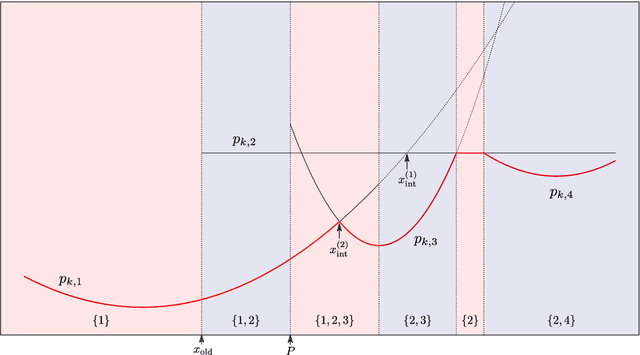
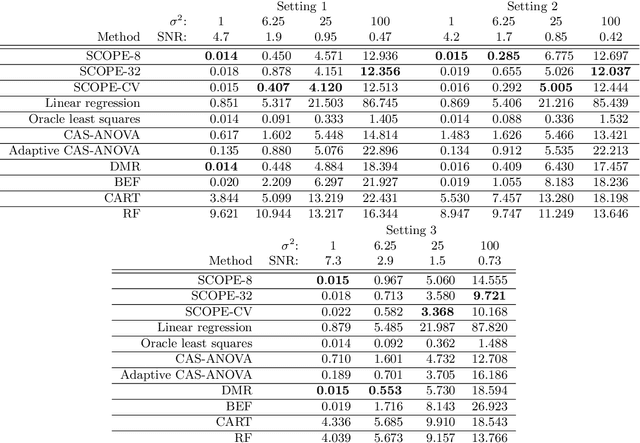
Abstract:We propose a method for estimation in high-dimensional linear models with nominal categorical data. Our estimator, called SCOPE, fuses levels together by making their corresponding coefficients exactly equal. This is achieved using the minimax concave penalty on differences between the order statistics of the coefficients for a categorical variable, thereby clustering the coefficients. We provide an algorithm for exact and efficient computation of the global minimum of the resulting nonconvex objective in the case with a single variable with potentially many levels, and use this within a block coordinate descent procedure in the multivariate case. We show that an oracle least squares solution that exploits the unknown level fusions is a limit point of the coordinate descent with high probability, provided the true levels have a certain minimum separation; these conditions are known to be minimal in the univariate case. We demonstrate the favourable performance of SCOPE across a range of real and simulated datasets. An R package CatReg implementing SCOPE for linear models and also a version for logistic regression is available on CRAN.
The xyz algorithm for fast interaction search in high-dimensional data
Sep 17, 2018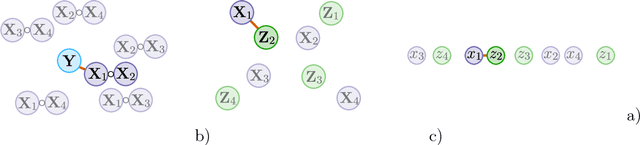
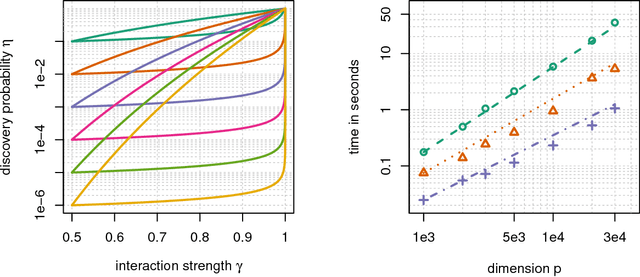
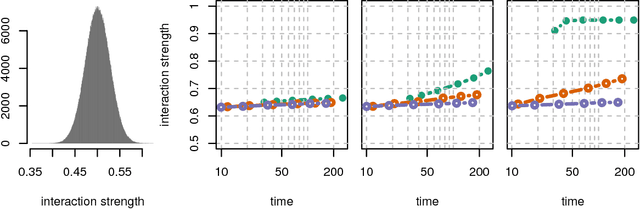
Abstract:When performing regression on a dataset with $p$ variables, it is often of interest to go beyond using main linear effects and include interactions as products between individual variables. For small-scale problems, these interactions can be computed explicitly but this leads to a computational complexity of at least $\mathcal{O}(p^2)$ if done naively. This cost can be prohibitive if $p$ is very large. We introduce a new randomised algorithm that is able to discover interactions with high probability and under mild conditions has a runtime that is subquadratic in $p$. We show that strong interactions can be discovered in almost linear time, whilst finding weaker interactions requires $\mathcal{O}(p^\alpha)$ operations for $1 < \alpha < 2$ depending on their strength. The underlying idea is to transform interaction search into a closestpair problem which can be solved efficiently in subquadratic time. The algorithm is called $\mathit{xyz}$ and is implemented in the language R. We demonstrate its efficiency for application to genome-wide association studies, where more than $10^{11}$ interactions can be screened in under $280$ seconds with a single-core $1.2$ GHz CPU.
On b-bit min-wise hashing for large-scale regression and classification with sparse data
Feb 26, 2018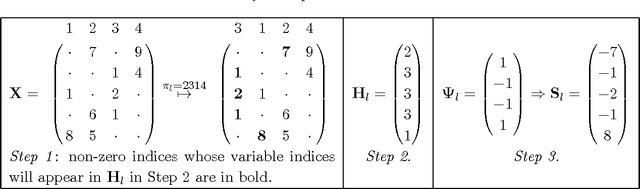
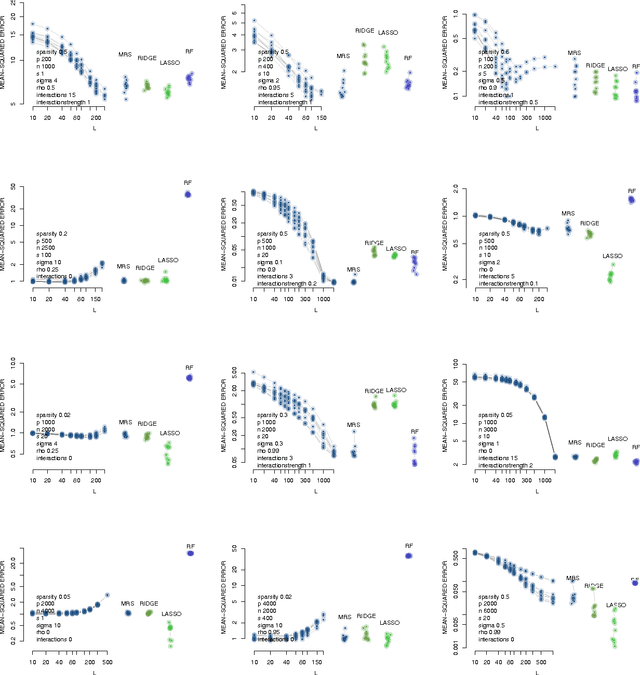
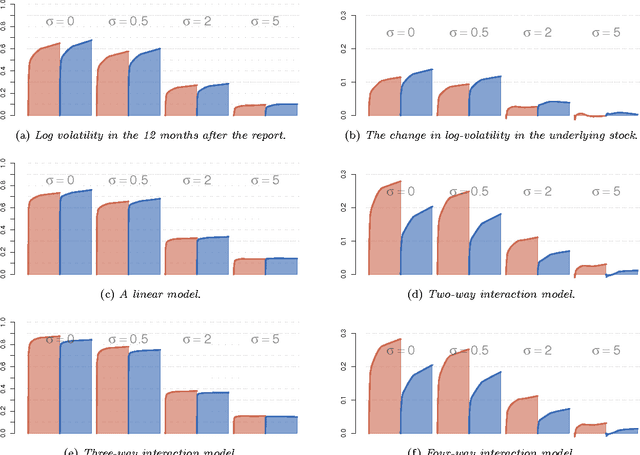
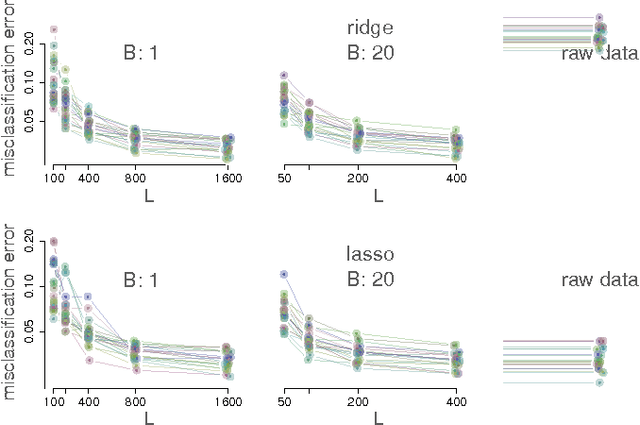
Abstract:Large-scale regression problems where both the number of variables, $p$, and the number of observations, $n$, may be large and in the order of millions or more, are becoming increasingly more common. Typically the data are sparse: only a fraction of a percent of the entries in the design matrix are non-zero. Nevertheless, often the only computationally feasible approach is to perform dimension reduction to obtain a new design matrix with far fewer columns and then work with this compressed data. $b$-bit min-wise hashing (Li and Konig, 2011) is a promising dimension reduction scheme for sparse matrices which produces a set of random features such that regression on the resulting design matrix approximates a kernel regression with the resemblance kernel. In this work, we derive bounds on the prediction error of such regressions. For both linear and logistic models we show that the average prediction error vanishes asymptotically as long as $q \|\beta^*\|_2^2 /n \rightarrow 0$, where $q$ is the average number of non-zero entries in each row of the design matrix and $\beta^*$ is the coefficient of the linear predictor. We also show that ordinary least squares or ridge regression applied to the reduced data can in fact allow us fit more flexible models. We obtain non-asymptotic prediction error bounds for interaction models and for models where an unknown row normalisation must be applied in order for the signal to be linear in the predictors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge