Gian-Andrea Thanei
The xyz algorithm for fast interaction search in high-dimensional data
Sep 17, 2018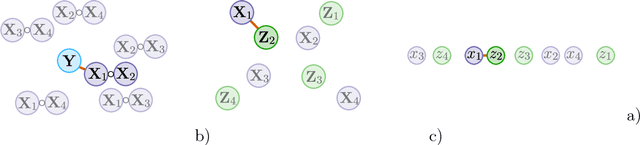
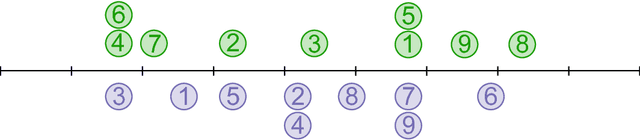
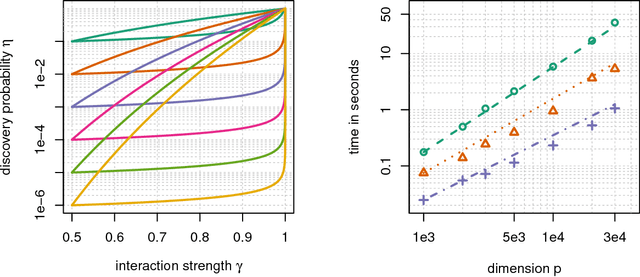
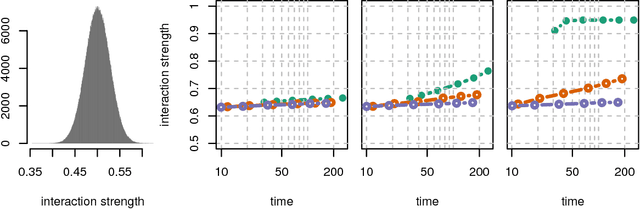
Abstract:When performing regression on a dataset with $p$ variables, it is often of interest to go beyond using main linear effects and include interactions as products between individual variables. For small-scale problems, these interactions can be computed explicitly but this leads to a computational complexity of at least $\mathcal{O}(p^2)$ if done naively. This cost can be prohibitive if $p$ is very large. We introduce a new randomised algorithm that is able to discover interactions with high probability and under mild conditions has a runtime that is subquadratic in $p$. We show that strong interactions can be discovered in almost linear time, whilst finding weaker interactions requires $\mathcal{O}(p^\alpha)$ operations for $1 < \alpha < 2$ depending on their strength. The underlying idea is to transform interaction search into a closestpair problem which can be solved efficiently in subquadratic time. The algorithm is called $\mathit{xyz}$ and is implemented in the language R. We demonstrate its efficiency for application to genome-wide association studies, where more than $10^{11}$ interactions can be screened in under $280$ seconds with a single-core $1.2$ GHz CPU.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge