Match Chat: Real Time Generative AI and Generative Computing for Tennis

We present Match Chat, a real-time, agent-driven assistant designed to enhance the tennis fan experience by delivering instant, accurate responses to match-related queries. Match Chat integrates Generative Artificial Intelligence (GenAI) with Generative Computing (GenComp) techniques to synthesize key insights during live tennis singles matches. The system debuted at the 2025 Wimbledon Championships and the 2025 US Open, where it provided about 1 million users with seamless access to streaming and static data through natural language queries. The architecture is grounded in an Agent-Oriented Architecture (AOA) combining rule engines, predictive models, and agents to pre-process and optimize user queries before passing them to GenAI components. The Match Chat system had an answer accuracy of 92.83% with an average response time of 6.25 seconds under loads of up to 120 requests per second (RPS). Over 96.08% of all queries were guided using interactive prompt design, contributing to a user experience that prioritized clarity, responsiveness, and minimal effort. The system was designed to mask architectural complexity, offering a frictionless and intuitive interface that required no onboarding or technical familiarity. Across both Grand Slam deployments, Match Chat maintained 100% uptime and supported nearly 1 million unique users, underscoring the scalability and reliability of the platform. This work introduces key design patterns for real-time, consumer-facing AI systems that emphasize speed, precision, and usability that highlights a practical path for deploying performant agentic systems in dynamic environments.

Automated Meta Prompt Engineering for Alignment with the Theory of Mind

We introduce a method of meta-prompting that jointly produces fluent text for complex tasks while optimizing the similarity of neural states between a human's mental expectation and a Large Language Model's (LLM) neural processing. A technique of agentic reinforcement learning is applied, in which an LLM as a Judge (LLMaaJ) teaches another LLM, through in-context learning, how to produce content by interpreting the intended and unintended generated text traits. To measure human mental beliefs around content production, users modify long form AI-generated text articles before publication at the US Open 2024 tennis Grand Slam. Now, an LLMaaJ can solve the Theory of Mind (ToM) alignment problem by anticipating and including human edits within the creation of text from an LLM. Throughout experimentation and by interpreting the results of a live production system, the expectations of human content reviewers had 100% of alignment with AI 53.8% of the time with an average iteration count of 4.38. The geometric interpretation of content traits such as factualness, novelty, repetitiveness, and relevancy over a Hilbert vector space combines spatial volume (all trait importance) with vertices alignment (individual trait relevance) enabled the LLMaaJ to optimize on Human ToM. This resulted in an increase in content quality by extending the coverage of tennis action. Our work that was deployed at the US Open 2024 has been used across other live events within sports and entertainment.

Finding Interest Needle in Popularity Haystack: Improving Retrieval by Modeling Item Exposure

Recommender systems operate in closed feedback loops, where user interactions reinforce popularity bias, leading to over-recommendation of already popular items while under-exposing niche or novel content. Existing bias mitigation methods, such as Inverse Propensity Scoring (IPS) and Off- Policy Correction (OPC), primarily operate at the ranking stage or during training, lacking explicit real-time control over exposure dynamics. In this work, we introduce an exposure- aware retrieval scoring approach, which explicitly models item exposure probability and adjusts retrieval-stage ranking at inference time. Unlike prior work, this method decouples exposure effects from engagement likelihood, enabling controlled trade-offs between fairness and engagement in large-scale recommendation platforms. We validate our approach through online A/B experiments in a real-world video recommendation system, demonstrating a 25% increase in uniquely retrieved items and a 40% reduction in the dominance of over-popular content, all while maintaining overall user engagement levels. Our results establish a scalable, deployable solution for mitigating popularity bias at the retrieval stage, offering a new paradigm for bias-aware personalization.

Nonparametric Estimation of Band-limited Probability Density Functions

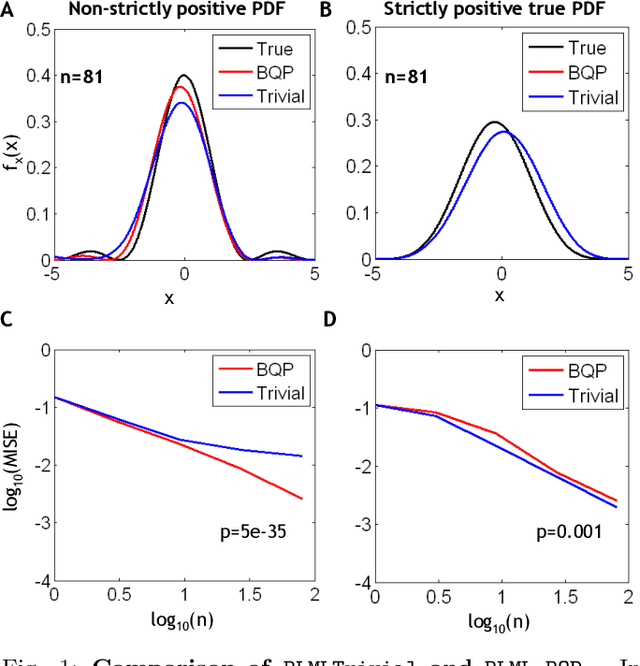
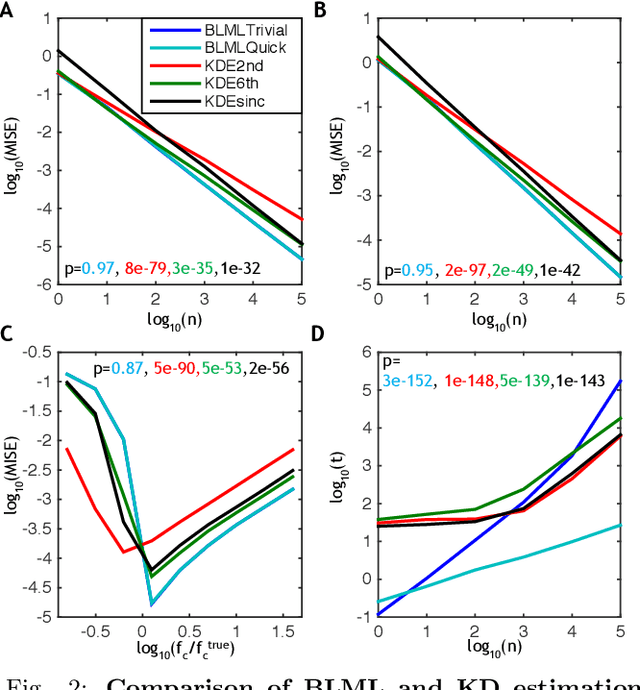
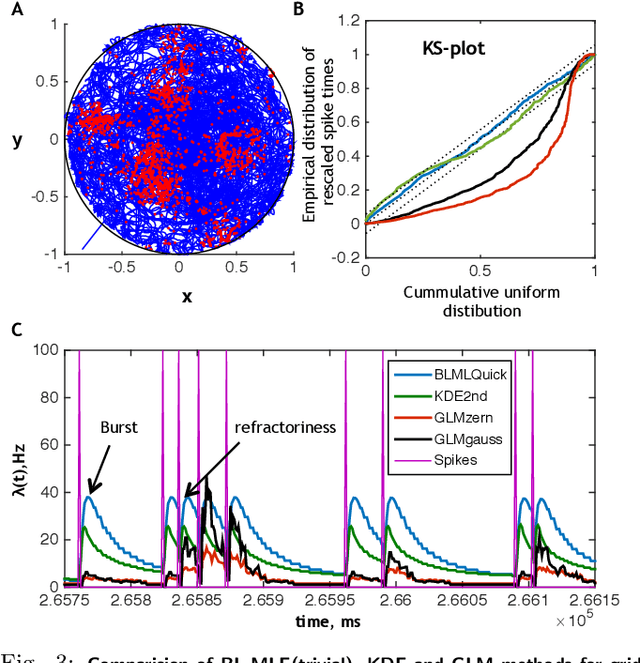
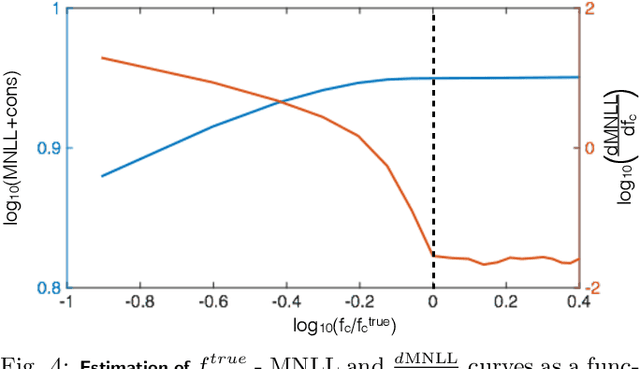
In this paper, a nonparametric maximum likelihood (ML) estimator for band-limited (BL) probability density functions (pdfs) is proposed. The BLML estimator is consistent and computationally efficient. To compute the BLML estimator, three approximate algorithms are presented: a binary quadratic programming (BQP) algorithm for medium scale problems, a Trivial algorithm for large-scale problems that yields a consistent estimate if the underlying pdf is strictly positive and BL, and a fast implementation of the Trivial algorithm that exploits the band-limited assumption and the Nyquist sampling theorem ("BLMLQuick"). All three BLML estimators outperform kernel density estimation (KDE) algorithms (adaptive and higher order KDEs) with respect to the mean integrated squared error for data generated from both BL and infinite-band pdfs. Further, the BLMLQuick estimate is remarkably faster than the KD algorithms. Finally, the BLML method is applied to estimate the conditional intensity function of a neuronal spike train (point process) recorded from a rat's entorhinal cortex grid cell, for which it outperforms state-of-the-art estimators used in neuroscience.

Mutual Dependence: A Novel Method for Computing Dependencies Between Random Variables

In data science, it is often required to estimate dependencies between different data sources. These dependencies are typically calculated using Pearson's correlation, distance correlation, and/or mutual information. However, none of these measures satisfy all the Granger's axioms for an "ideal measure". One such ideal measure, proposed by Granger himself, calculates the Bhattacharyya distance between the joint probability density function (pdf) and the product of marginal pdfs. We call this measure the mutual dependence. However, to date this measure has not been directly computable from data. In this paper, we use our recently introduced maximum likelihood non-parametric estimator for band-limited pdfs, to compute the mutual dependence directly from the data. We construct the estimator of mutual dependence and compare its performance to standard measures (Pearson's and distance correlation) for different known pdfs by computing convergence rates, computational complexity, and the ability to capture nonlinear dependencies. Our mutual dependence estimator requires fewer samples to converge to theoretical values, is faster to compute, and captures more complex dependencies than standard measures.