Geometric Scaling of Bayesian Inference in LLMs

Recent work has shown that small transformers trained in controlled "wind-tunnel'' settings can implement exact Bayesian inference, and that their training dynamics produce a geometric substrate -- low-dimensional value manifolds and progressively orthogonal keys -- that encodes posterior structure. We investigate whether this geometric signature persists in production-grade language models. Across Pythia, Phi-2, Llama-3, and Mistral families, we find that last-layer value representations organize along a single dominant axis whose position strongly correlates with predictive entropy, and that domain-restricted prompts collapse this structure into the same low-dimensional manifolds observed in synthetic settings. To probe the role of this geometry, we perform targeted interventions on the entropy-aligned axis of Pythia-410M during in-context learning. Removing or perturbing this axis selectively disrupts the local uncertainty geometry, whereas matched random-axis interventions leave it intact. However, these single-layer manipulations do not produce proportionally specific degradation in Bayesian-like behavior, indicating that the geometry is a privileged readout of uncertainty rather than a singular computational bottleneck. Taken together, our results show that modern language models preserve the geometric substrate that enables Bayesian inference in wind tunnels, and organize their approximate Bayesian updates along this substrate.

The Bayesian Geometry of Transformer Attention

Transformers often appear to perform Bayesian reasoning in context, but verifying this rigorously has been impossible: natural data lack analytic posteriors, and large models conflate reasoning with memorization. We address this by constructing \emph{Bayesian wind tunnels} -- controlled environments where the true posterior is known in closed form and memorization is provably impossible. In these settings, small transformers reproduce Bayesian posteriors with $10^{-3}$-$10^{-4}$ bit accuracy, while capacity-matched MLPs fail by orders of magnitude, establishing a clear architectural separation. Across two tasks -- bijection elimination and Hidden Markov Model (HMM) state tracking -- we find that transformers implement Bayesian inference through a consistent geometric mechanism: residual streams serve as the belief substrate, feed-forward networks perform the posterior update, and attention provides content-addressable routing. Geometric diagnostics reveal orthogonal key bases, progressive query-key alignment, and a low-dimensional value manifold parameterized by posterior entropy. During training this manifold unfurls while attention patterns remain stable, a \emph{frame-precision dissociation} predicted by recent gradient analyses. Taken together, these results demonstrate that hierarchical attention realizes Bayesian inference by geometric design, explaining both the necessity of attention and the failure of flat architectures. Bayesian wind tunnels provide a foundation for mechanistically connecting small, verifiable systems to reasoning phenomena observed in large language models.

Gradient Dynamics of Attention: How Cross-Entropy Sculpts Bayesian Manifolds

Transformers empirically perform precise probabilistic reasoning in carefully constructed ``Bayesian wind tunnels'' and in large-scale language models, yet the mechanisms by which gradient-based learning creates the required internal geometry remain opaque. We provide a complete first-order analysis of how cross-entropy training reshapes attention scores and value vectors in a transformer attention head. Our core result is an \emph{advantage-based routing law} for attention scores, \[ \frac{\partial L}{\partial s_{ij}} = α_{ij}\bigl(b_{ij}-\mathbb{E}_{α_i}[b]\bigr), \qquad b_{ij} := u_i^\top v_j, \] coupled with a \emph{responsibility-weighted update} for values, \[ Δv_j = -η\sum_i α_{ij} u_i, \] where $u_i$ is the upstream gradient at position $i$ and $α_{ij}$ are attention weights. These equations induce a positive feedback loop in which routing and content specialize together: queries route more strongly to values that are above-average for their error signal, and those values are pulled toward the queries that use them. We show that this coupled specialization behaves like a two-timescale EM procedure: attention weights implement an E-step (soft responsibilities), while values implement an M-step (responsibility-weighted prototype updates), with queries and keys adjusting the hypothesis frame. Through controlled simulations, including a sticky Markov-chain task where we compare a closed-form EM-style update to standard SGD, we demonstrate that the same gradient dynamics that minimize cross-entropy also sculpt the low-dimensional manifolds identified in our companion work as implementing Bayesian inference. This yields a unified picture in which optimization (gradient flow) gives rise to geometry (Bayesian manifolds), which in turn supports function (in-context probabilistic reasoning).

ClusterSC: Advancing Synthetic Control with Donor Selection

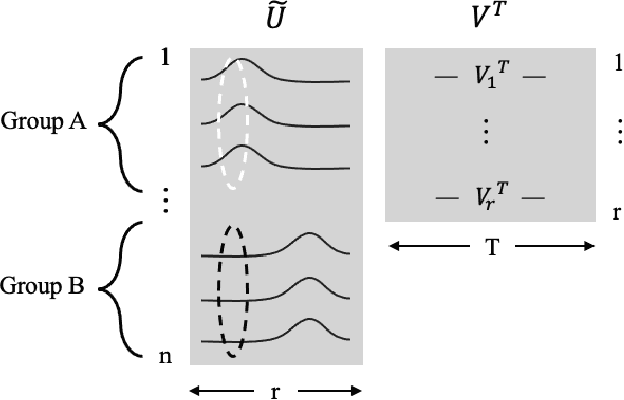
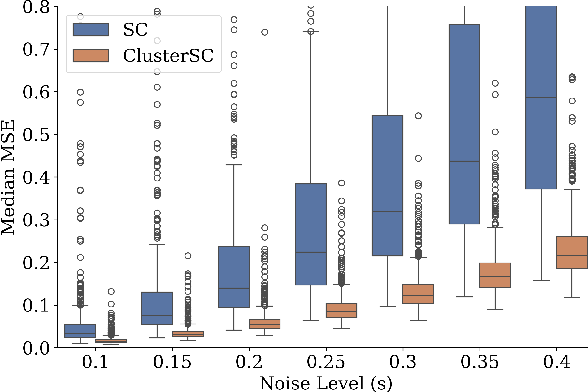
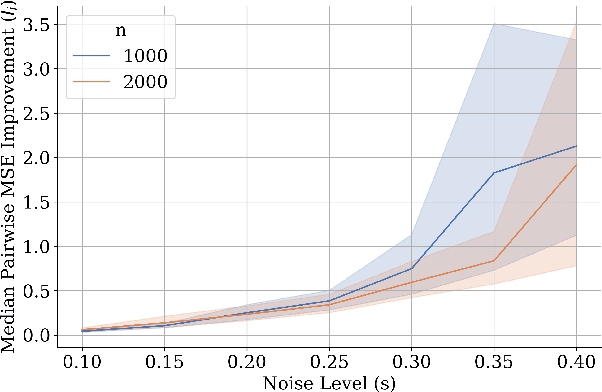
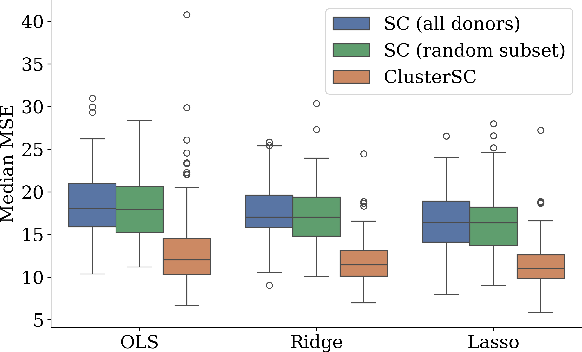
In causal inference with observational studies, synthetic control (SC) has emerged as a prominent tool. SC has traditionally been applied to aggregate-level datasets, but more recent work has extended its use to individual-level data. As they contain a greater number of observed units, this shift introduces the curse of dimensionality to SC. To address this, we propose Cluster Synthetic Control (ClusterSC), based on the idea that groups of individuals may exist where behavior aligns internally but diverges between groups. ClusterSC incorporates a clustering step to select only the relevant donors for the target. We provide theoretical guarantees on the improvements induced by ClusterSC, supported by empirical demonstrations on synthetic and real-world datasets. The results indicate that ClusterSC consistently outperforms classical SC approaches.

The Matrix: A Bayesian learning model for LLMs

In this paper, we introduce a Bayesian learning model to understand the behavior of Large Language Models (LLMs). We explore the optimization metric of LLMs, which is based on predicting the next token, and develop a novel model grounded in this principle. Our approach involves constructing an ideal generative text model represented by a multinomial transition probability matrix with a prior, and we examine how LLMs approximate this matrix. We discuss the continuity of the mapping between embeddings and multinomial distributions, and present the Dirichlet approximation theorem to approximate any prior. Additionally, we demonstrate how text generation by LLMs aligns with Bayesian learning principles and delve into the implications for in-context learning, specifically explaining why in-context learning emerges in larger models where prompts are considered as samples to be updated. Our findings indicate that the behavior of LLMs is consistent with Bayesian Learning, offering new insights into their functioning and potential applications.

Predicting Ground Reaction Force from Inertial Sensors

The study of ground reaction forces (GRF) is used to characterize the mechanical loading experienced by individuals in movements such as running, which is clinically applicable to identify athletes at risk for stress-related injuries. Our aim in this paper is to determine if data collected with inertial measurement units (IMUs), that can be worn by athletes during outdoor runs, can be used to predict GRF with sufficient accuracy to allow the analysis of its derived biomechanical variables (e.g., contact time and loading rate). In this paper, we consider lightweight approaches in contrast to state-of-the-art prediction using LSTM neural networks. Specifically, we compare use of LSTMs to k-Nearest Neighbors (KNN) regression as well as propose a novel solution, SVD Embedding Regression (SER), using linear regression between singular value decomposition embeddings of IMUs data (input) and GRF data (output). We evaluate the accuracy of these techniques when using training data collected from different athletes, from the same athlete, or both, and we explore the use of acceleration and angular velocity data from sensors at different locations (sacrum and shanks). Our results illustrate that simple machine learning methods such as SER and KNN can be similarly accurate or more accurate than LSTM neural networks, with much faster training times and hyperparameter optimization; in particular, SER and KNN are more accurate when personal training data are available, and KNN comes with benefit of providing provenance of prediction. Notably, the use of personal data reduces prediction errors of all methods for most biomechanical variables.

Differentially Private Synthetic Control

Synthetic control is a causal inference tool used to estimate the treatment effects of an intervention by creating synthetic counterfactual data. This approach combines measurements from other similar observations (i.e., donor pool ) to predict a counterfactual time series of interest (i.e., target unit) by analyzing the relationship between the target and the donor pool before the intervention. As synthetic control tools are increasingly applied to sensitive or proprietary data, formal privacy protections are often required. In this work, we provide the first algorithms for differentially private synthetic control with explicit error bounds. Our approach builds upon tools from non-private synthetic control and differentially private empirical risk minimization. We provide upper and lower bounds on the sensitivity of the synthetic control query and provide explicit error bounds on the accuracy of our private synthetic control algorithms. We show that our algorithms produce accurate predictions for the target unit, and that the cost of privacy is small. Finally, we empirically evaluate the performance of our algorithm, and show favorable performance in a variety of parameter regimes, as well as providing guidance to practitioners for hyperparameter tuning.